Рассмотрим шестизвенный механизм, положение 1 - рабочий ход. Рассмотрим выходную группу звеньев 5 — 4. Выделим суппорт 5, обозначая все действующие на пего силы (рисунок 11).
Рисунок 11 — Силы, действующие на суппорт 5
Сила инерции суппорта Ф5 приложена в его центре масс и направлена в сторону, противоположную ускорению aD5.
Равнодействующая сил тяжести суппорта G5 также приложена в центре масс и направлена вертикально вниз. Сила реакции R45 со стороны кулисного камня 4 на суппорт 5 приложена в точке D, так как кулисный камень имеет малые линейные
размеры, и направлена под прямым углам к поверхности, вдоль которой перемещается кулисный камень 4.
Равнодействующая R05 сил реакции стойки Е, направлена под прямым углом к поверхности, вдоль которой перемещается суппорт, но плечо k этой силы относительно центра масс суппорта неизвестно. Проанализировав характер нагрузки на суппорт 5, заключаем, что необходимо определить три неизвестные величины: модули сил реакций R45,R05 и величину плеча k. Для этого необходимо составить и решить три независимых уравнения кинетостатики звена.
Уравнение равновесия сил в горизонтальном направлении имеет вид (силы, направленные вправо, учитываются со знаком «+»):
Fс+Ф5-Rx45=0,
где Fc — сила сопротивления (резания), передаваемая от резца со стороны обрабатываемой детали;
Ф5 — сила инерции суппорта 5;
Rx45 - проекция на горизонтальное направление силы реакции со стороны
кулисного камня 4 на суппорт 5.
Ф5 = т5 * aD5,
где m 5 — масса суппорта 5;
aD5 — ускорение центра масс суппорта 5.
Ф5 =20*20,16=403,2 (Н)
Откуда, выражая Rx45, получаем:
Rx45 =Fc+Ф5
Rx45 =1000+403,2=1403,2 (Н)
Уравнение сил в вертикальном направлении имеет вид (силы, направленные вверх, учитываются со знаком «+»):
R05 - G5 + Ry45= 0,
где R05 - равнодействующая сил реакции стойки Е;
G5 — равнодействующая сил тяжести суппорта 5;
Ry45 - проекция на вертикальное направление силы реакции со стороны кулисного камня 4 на суппорт 5.
Ry45 = Rx45 * tan(12°34`),
где Rx45 — проекция на горизонтальное направление силы реакции со стороны кулисного камня 4 на суппорт 5.
Ry45 = 1403,2*tan(12°34`)=312.8(Н)
G5 = m5 * g,
где m5 — масса суппорта 5;
g — ускорение свободного падения, равное 9.81 м/с2.
G5 =20*9.81=196.2 (Н)
Откуда, выражая R05 получаем:
R05=G5- Ry45
R05 =196.2-312.8=-116.6(Н)
Найдем полную реакцию со стороны кулисного камня 4 на суппорт 5:
где Rx45 — проекция на горизонтальное направление силы реакции со стороны кулисного камня 4 на суппорт 5;
Ry45 - проекция на вертикальное направление силы реакции со стороны кулисного камня 4 на суппорт 5.
R45=542.9 (Н)
Уравнение моментов относительно центра масс S5 суппорта 5 имеет вид
(моменты сил, действующие против часовой стрелки, учитываются со знаком «+»):
-R05 * k + Ry45 * l S5D = 0,
где R05— равнодействующая сил реакции стойки Е;
k - плечо действия силы Р45 относительно центра масс суппорта 5;
Ry45 - проекция на вертикальное направление силы реакции со стороны кулисного камня 4 на суппорт 5;
l S5D — плечо действия силы Ry45, равное 0.28 м.
Откуда, выражая k, получаем:
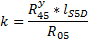k =0.75 (м)
Рассмотрим групп у звеньев 3 -2 (рисунок 12)
Реакция R12 со стороны кривошипа 1 на шатун 2 неизвестна ни по направлению, ни по модулю. Разложим ее на составляющие: Rτ12 - проекция реакции силы R12 в направлении перпендикулярном АВ, Rn12 - проекция реакции силы R12 в направлении параллельном АВ. Равнодействующая сил тяжести G2 приложена в центре масс шатуна 2 и направлена вертикально вниз. Сила инерции Ф2 прилажена в центре масс шатуна 2 и направлена в сторону противоположную ускорению центра масс шатуна 2. Момент сил инерции М2 шатуна 2 направлен в сторону противоположную угловому ускорению звена 2. Момент сил инерции кулисы 3 направлен в сторону противоположную угловому ускорению звена 3.
Сила инерции Ф3 приложена в центре масс кулисы 3 и направлена в сторону противоположную ускорению центра масс кулисы З. Равнодействующая сил тяжести G3 приложена в центре масс кулисы 3 и направлена вертикально вниз. Реакция R03 со стороны стойки на звено 3 неизвестна ни по направлению, ни по модулю. Разложим ее на составляющие: Rτ03 - проекция реакции силы R03 в направлении перпендикулярном СВ, Rn03 - проекция реакции силы R03 в направлении параллельном СВ. Сила реакции R43 со стороны кулисного камня 4 приложена в точке D, так как кулисный камень имеет малые линейные размеры, и сила R43направлена под прямым углом к поверхности, вдоль которой перемещается кулисный камень 4. Сила реакции R43равна по модулю и противоположна по направлению реакции R45.
Вычислим значения сил.
G2=m2*g
где m2 - масса шатуна 2;
g - ускорение свободного падения, равное 9.81 м/с2.
G2 = 13*9.81=127.53(Н)
Ф2= m2*as2
где m2 - масса шатуна 2;
аs2 ускорение центра масс шатуна 2.
Где lAS2 - расстояние от точки А до центра масс шатуна 2;
lAB - длина шатуна 2;
аBA - ускорение точки В относительно точки А.
аs2= 
(м/c2)
Таким образом, получаем:
Ф2 =13*5.89=76.6 (H)
М2 = Js2 * ℰ2,
где Js2 - собственный момент инерции шатуна 2;
ℰ2 - угловое ускорение шатуна 2;
М2 =0.14*47,7=6.678 (Н*м)
М3 = Js3 * ℰ3,
где Js3 - собственный момент инерции звена;
ℰ3 - угловое ускорение звена;
М3 =0.33*159=52.47 (Н*м)
G3=m3*g
где m3 - масса звена 3;
g - ускорение свободного падения, равное 9.81 м/ег.
G3= 18*9.81=176.58(Н)
Ф3 =m3* as3
где m3 - масса звена 3;
аS3 - ускорение центра масс звена.
где lСS3 - расстояние от точки С до центра масс звена 3;
lCB - длина кулисы 3;
аB - ускорение точки В. принадлежащей шатуну 2 и кулисе 3.
аS3 = 
(м/с2)
Таким образом, получаем:
Ф3 =6.36*18=114.48 (Н)
Составим уравнение моментов относительно точки В звена 2:
-Rτ12*lAB +G2*h2-Ф2*h1 +М2 =0,
гдеRτ12 - проекция реакции силы 1?12 в направлении перпендикулярном АВ;
lAB - длина шатуна 2;
G2 - Равнодействующая сил тяжести шатуна 2;
h2 - плечо действия силы G2, равное мм;
Ф2 - сила инерции шатуна 2;
h 1 - плечо действия силы Ф2, равное мм;
М2 - момент силы инерции шатуна 2.
Выражая Rτ12, получаем:
Rτ12 = 
(H)
Составим уравнение моментов относительно точки В звена 3:
Rτ03*lвс-Gз*h3+Фз*h4-Мз-R43*h5 =0,
где Rτ03 - проекция реакции силы R03 в направлении перпендикулярном ВС;
lвс - длина коромысла 3;
Gз - равнодействующая сил тяжести звена 3;
h3 - плечо действия силы G3, равное 85.92 мм;
Ф3 - сила инерции звена 3;
h4 - плечо действия силы Ф3, равное 160мм;
М3 - момент силы инерции звена 3;
R43 - сила реакции со стороны кулисного камня 4 на кулисе 3, равная по модулю R45;
h5 - плечо действия силы R43, равное 47.96мм.
Выражая Rτ03, получаем:
Rτ03= 
(H)
Для нахождения оставшихся сил реакций Rn12 и Rn03 построим план сил в масштабе µЕ = 5 (Н/мм). Векторное уравнение имеет вид:
где 
- проекция реакции силы R12 в направлении параллельном ВС;
- проекция реакции силы R12 в направлении перпендикулярном АВ;
- равнодействующая сил тяжести шатуна 2;
- сила инерции шатуна 2;
- сила реакции со стороны кулисного камня 4 на кулису 3, равная по модулю R45;
- сила инерции звена 3;
- равнодействующая сил тяжести звена 3;
- проекция реакции силы R03 в направлении перпендикулярном ВС;
- проекция реакции силы R03 в направлении параллельном ВС.
Откуда получаем, что отрезок, изображающий реакцию Rn12 равен 92.06мм, а отрезок, изображающий реакцию Rn03 равен 137.5мм, тогда:
Rn12 = 128,2* µF
где µF - масштабный коэффициент плана сил.
Rn12 =128,2*5=641(Н)
Rn03 = 158.04* µF
где µF - масштабный коэффициент плана сил.
Rn03 = 158,04*5=790(Н)
Вычислим значения сил реакций R12 и R03. Отрезки, изображающие эти реакции на плане сил, равны 92.3мм и 138.6мм Соответственно, тогда:
R12= 128,4* µF,
Где µF - масштабный коэффициент плана сил.
R12 =128,4*5=641,8 (Н)
R03 = 149,4* µF,
где µF - масштабный коэффициент плана сил.
R03= 149,4*5=747(Н)
Отбросим шатун 2 и заменим его действие силой реакции R23(Рисунок 13).
Рисунок 13 - Силы, действующие на звено 3
Вычислим величину этой реакции, для чего построим план сил в масштабе µF = 5 (Н/мм). Векторное уравнение имеет вид:
где 
- сила реакции со стороны шатуна 2 на кулису 3;
- сила инерции звена 3;
- равнодействующая сил тяжести звена 3;
- сила реакции со стороны стойки на звено 3;
- сила реакции со стороны кулисного камня 4 на кулису 3, равная по модулю R45.
Откуда получаем, что отрезок, изображающий реакцию R23 равен 110.5 мм, тогда:
R23 = 110.5* µF,
где µF - масштабный коэффициент плана сил.
R23 =110.5*5=552.5 (Н)
Рассмотрим начальную группу звеньев «стойка-кривошип». Выделим кривошип 1, обозначив все действующие на него силы (рисунок 14).
Рисунок 14 - Силы, действующие на кривошип 1
Реакция R21 со стороны шатуна 2 на кривошип 1, равная по модулю R12Инаправленная в противополож1ryю сторону; реакция со стороны стойки R01, не известная ни по модулю, ни по направлению и движущий момент Мдв., не известный по величине.
Найдем неизвестные величины. Равнодействующая сил тяжести кривошипа 1 равна:
G1=m1*g
где m1 — масса кривошипа 1;
g — ускорение свободного падения, равное 9.81 м/с'.
G1 = 7*9.81=68.67(Н)
Движущий момент Мдв. найдем из уравнения моментов относительно точки O:
- Мдв. + R21 * h0 = 0,
где Мдв, — движущий момент;
R21 — сила реакции со стороны шатуна 2 на кривошип 1, равная по модулю R12;
h0 — плечо действия силы R21, равное 30.58мм.
Выражая Мдв., получим:
Мдв= R21*h0
Мдв . = 641,8*30.58* 
=19,62(Н*м)
Реакцию R01 определим, построив план сил в масштабе µF = 5 (Н/мм).
Векторное уравнение сил, действующих на кривошип 1, имеет вид:
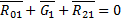
Где 
- сила реакции со стороны стойки 0 на кривошип 1;
— равнодействующая сил тяжести кривошипа 1;
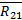— сила реакции со стороны шатуна 2 на кривошип 1, равная по модулю R12.
Откуда получаем, что отрезок, изображающий реакцию R01 равен 41.16 мм,
тогда:
R01 = 41.16* µF,
где µF - масштабный коэффициент плана сил.
R01 = 41.16*5=205.8(Н)
Обобщенные результаты вычислений приведены в Таблице 7. Таблица 7
| Величина | Значение |
| Fc(Н) | |
| K(м) | 0.75 |
| G1(Н) | 68.67 |
| G2(Н) | 127.53 |
| G3(Н) | 176.53 |
| G5(Н) | 196.2 |
| Ф2(Н) | 76.6 |
| Ф3(Н) | 114.48 |
| Ф5(Н) | 403.2 |
| R01(Н) | 205.8 |
| R12(Н) | 641,8 |
| R23(Н) | 552.5 |
| R03(Н) | |
| R43(Н) | 542.9 |
| R45(Н) | 542.9 |
| R05(Н) | 116.6 |
| Mдв. (Н*м) | 19,62 |
