БЛОК 3



Б3. 6. Операторы в нормированном пространтсве
ОПР1. Линейное пространство L называется нормированным, если любому его элементу x поставлено в соответствие число, называемое нормой и обозначаемое  , причем при этом выполнены следующие условия:
, причем при этом выполнены следующие условия:

Всякое нормированное пространство становится метрическим, если ввести в нем расстояние 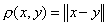 . Справедливость аксиом метрического пространства вытекает из свойств 1) – 3) нормы. На нормированные пространства переносятся, таким образом, все понятия и факты, которые были изложены для метрических пространств.
. Справедливость аксиом метрического пространства вытекает из свойств 1) – 3) нормы. На нормированные пространства переносятся, таким образом, все понятия и факты, которые были изложены для метрических пространств.
ОПР. Полное нормированное пространство называется банаховым пространством.
ОПР: Оператором называется отображение  где
где  - некоторые пространства.
- некоторые пространства.
Область определения оператора  - множество, на котором задано действие оператора, область значений оператора
- множество, на котором задано действие оператора, область значений оператора  .
.
Обычно мы будем иметь дело со случаем H=G.
ОПР: Операторы  называются равными, если:
называются равными, если:

ОПР: Оператор  называется расширением А, а А – сужением
называется расширением А, а А – сужением  (обозначается
(обозначается  ), если:
), если: 
ОПР: Оператор А называется непрерывным в точке  если для всякого
если для всякого  найдется такое
найдется такое  , что
, что  если
если 
ОПР: Оператор А называется непрерывным, если он непрерывен в каждой точке D (A).
ОПР: Линейный оператор –это многомерный аналог функции одной переменной, графиком которой служит прямая, проходящая через начало координат, то есть функций  для некоторого
для некоторого  .
.
ОПР: Оператор L с областью определения D (L) называется линейным, если для всех  и всех
и всех 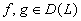 :
:

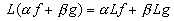 .
.
Многие и весьма разнообразные уравнения представимы в виде 
Где L – линейный оператор.
Пусть А – линейный оператор. Будем говорить, что А имеет обратный, если для каждого 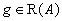 существует точно одно
существует точно одно 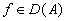 , такое что
, такое что 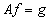 . При этом под обратным понимается оператор с областью определения
. При этом под обратным понимается оператор с областью определения  и множество значений D (A), заданный соотношением
и множество значений D (A), заданный соотношением  где
где 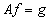 .
.
Вопрос существования обратного оператора – это вопрос об условиях разрешимости операторного уравнения 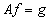 (*)
(*)
В конечномерном случае эти условия формулировала альтернатива Фредгольма.
Теорема Фредгольма (альтернатива).
Если уравнение  имеет только тривиальное решение, то уравнение (*) разрешимо единственным образом при любой правой части.
имеет только тривиальное решение, то уравнение (*) разрешимо единственным образом при любой правой части.
Теорема Фредгольма.
Если уравнение  имеет нетривиальное решение, то (*) разрешимо (заведомо не единственным образом) тогда и только тогда, когда
имеет нетривиальное решение, то (*) разрешимо (заведомо не единственным образом) тогда и только тогда, когда  ортогональна всем решениям сопряженной однородной задачи.
ортогональна всем решениям сопряженной однородной задачи.
Линейный оператор А называется ограниченным, если существует  такое, что для любого
такое, что для любого 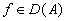 :
: 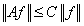 .
.
Точная нижняя грань inf (С) всех чисел С,для которых выполняется это неравенство, обозначается  и называется нормой оператора. Равносильное определение
и называется нормой оператора. Равносильное определение  таково:
таково:

 .
. 
Приведем несколько свойств ограниченных операторов.
Лемма 1. Если линейный оператор непрерывен в некоторой точке 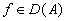 , то он непрерывен на D (A).
, то он непрерывен на D (A).
Лемма 2. Для линейных операторов непрерывность равносильна ограниченности.
Пример неограниченного оператора.
 . Пусть
. Пусть 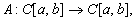


Для ограниченного оператора существует  , следовательно, доказывать можно “от противного “.
, следовательно, доказывать можно “от противного “.
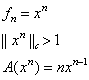
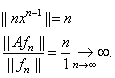
Доказано.
Б3. 7. Непрерывные и ограниченные операторы

Определение: Оператор  ограничен, если
ограничен, если  .
.
Определение: Оператор  непрерывен в точке
непрерывен в точке  , если
, если  .
.


Теорема: Линейный оператор непрерывен тогда и только тогда, когда он ограничен. Доказательство:
1.  — ограничен, значит,
— ограничен, значит, 

 .
.
А непрерывен в 0, следовательно, непрерывен и на X.
2. Пусть  — непрерывен на X, в частности, в
— непрерывен на X, в частности, в  , тогда:
, тогда:
Подставляем в определение 
§ Для  условие ограничения будет соблюдено при любом
условие ограничения будет соблюдено при любом  .
.
§ Для  рассмотрим рассмотрим   Но
Но  . Значит, . Значит, 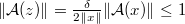 , таким образом, , таким образом, 
|
Выберем  , и получим, что оператор ограничен.
, и получим, что оператор ограничен.




