ЛЕКЦИЯ 25
Расчет целиков
Расчет целиков по гипотезе Турнера-Шевякова
Условие предельного равновесия пород можно записать следующим образом
Для ленточного целика - 
где а и b - соответственно ширина камеры и целика.
Откуда
Для столбчатых целиков квадратной и прямоугольной формы выражение можно записать соответственно:
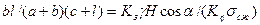
где l - длина целика.
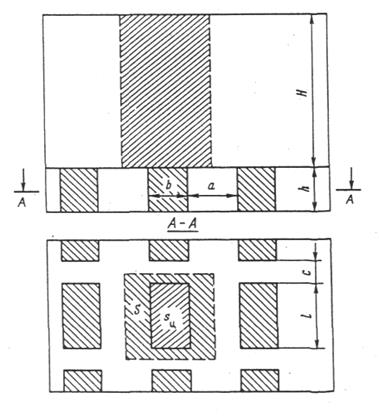
Схема к определению давления на целики по методу Турнера - Шевякова (целики прямоугольного сечения)
Решая эти уравнения относительно b, можно найти ширину целика, обеспечивающего устойчивое состояние вышележащих пород. Значение 
Л.Д. Шевяков рекомендовал принимать от 1,3-1,5 до3-5 в зависимости от свойств пород и условий работы целиков
Отмечая простоту и доступность изложенного метода, необходимо отметить следующие его недостатки:
в расчетах предполагается равномерное распределение напряжений по всей площади сечения целика;
при определении веса столба пород, приходящихся на целик, игнорируется его связь с окружающим массивом и, таким образом, не учитывается соотношение подработанной площади и глубины разработки;
предел прочности сжатия материала целика принимается для случая одноосного сжатия;
не учитывается влияние горизонтальных (тектонических) сил.
Следовательно, размеры целиков, вычисленные по методу Турнера-Шевякова, могут быть несколько завышенными. Рассчитывать целики в этом случае рекомендуется при отношении пролета подработки пород к глубине работ не менее 0,7-0,8.
Расчет целиков при наклонном залегании рудных тел
|
При разработке наклонных залежей оставляются междукамерные и междуэтажные целики. Первые располагаются по восстанию и могут быть в виде лент или столбов, вторые - как правило, ленточные. Эти целики находятся под воздействием вертикальных и горизонтальных сил, в результате чего в них возникают как нормальные, так и касательные напряжения. По методике Н.Н. Куваева действующая сверху распределенная нагрузка γH в нормальном сечении целика представляется в виде равнодействующей
Схема к расчету размеров целиков при наклонном залегании рудных тел
где S=(a+l)(b+l’) - площадь пород, приходящихся на целик; γ удельный вес налегающих пород; a и l - соответственно ширина целика и камеры по восстанию; b и lэ - соответственно длина целика и камеры по простиранию; α - угол падения залежи; H- мощность налегающих пород.
Горизонтально действующую силу 
при коэффициенте бокового распора m можно определить из выражения
PH=m γ H S sinα
Разложение сил Рv и РH на нормальную и касательную составляющие, позволяет получить следующие системы равенств:
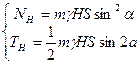
из которых можно найти нормальные σ и сдвигающие τ напряжения в целике:
После преобразований выражений можно записать следующее:
Прочные размеры целика на сжатие определяются на основании неравенства:
.
Устойчивость целика определяется отношением τ/σ>f. Если τ/σ>f (где f - коэффициент трения по плоскости контакта целиками с породами), то положение целика будет устойчивым, а при τ/σ>f он будет сдвигаться по плоскости ослабления. Угол трения φ определяется в зависимости от характера плоскости ослабления. Например, при наличии глинистого или сланцевого материала φ изменяется от 10˚ до 30˚.
Направление равнодействующей силы R отклоняется от нормали к напластованию на угол β, поэтому для большей устойчивости ось целика рекомендуется располагать не по нормали к лежачему и висячему бокам, а под углом β.
Значение равнодействующей силы в этом случае определяется из выражения
,
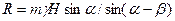а нормальные напряжения в сечении, перпендикулярном оси целика, по формуле
или
,
где 
.
Расположение целика по направлению равнодействующей силы R.
Увеличение угла падения залежи приводит к снижению действующих на целик нормальных напряжений, которое можно характеризовать коэффициентом угла падения Ка в случае расположения целика по оси R.
,
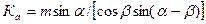а при расположении целиков перпендикулярно к висячему и лежачему бокам
.
