Первая теорема подобия (теорема Ньютона, 1686г.)

Теория подобия и применение к изучению КТО. Теоремы подобия.

Теория подобия

Теория подобия – это учение о подобных явлениях.

 

Теория подобия позволяет:

· объединять размерные величины в безразмерные комплексы;

· сокращать число переменных под знаком функции;

· устанавливать условия переноса результатов экспериментов на другие объекты.

 

Подобными физическими явлениями называются такие явления, которые проходят в геометрически подобных системах, то есть, если два явления подобны, первое из них описывается уравнением , а второе - уравнением 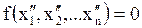, то существует набор констант подобия, представляющих собой отношение одноименных физических величин в сходственных точках пространства в сходственные моменты времени:

.

 

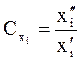ПРИМЕР ПОЛУЧЕНИЯ ЧИСЛА ПОДОБИЯ Nu

 

Воспользуемся дифференциальным уравнением теплоотдачи.

 

для первой системы:для второй системы:

 

, .

 

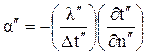Обозначим константы подобия:

 

,

где ℓ- характерный размер системы.

 

.

 

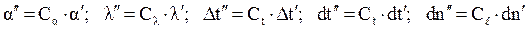Подставив эти выражения в уравнение и сократив на С_t, получаем

 

.

 

Их определенная комбинация, обусловленная видом исходного уравнения, описывающего данный физический процесс, должна быть равна единице. Соотношение получило название индикатора подобия.

 

Заменив значения констант подобия, получаем

.

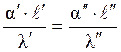Эти безразмерные соотношения называют числами (или критериями) подобия.

 

Записанное уравнением число называют числом Нуссельта и обозначают Nu.

.

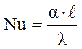Применение теории подобия к КТО

Уравнения подобия конвективного теплообмена

Уравнением подобия называется зависимость между каким-либо определяемым числом подобия и другими определяющими числами подобия.

 

(Gри решении задач на КТО искомым является a (только с его помощью можно воспользоваться уравнением Ньютона-Рихмана и рассчитать тепловые потоки), то определяемым числом подобия является Nu (только в это число входит a). Прочие числа подобия (Re, Gr, Pr, Fo) являются определяющими - с их помощью рассчитывается численное значение Nu.)

 

При конвективном теплообмене уравнение подобия в общем случае имеет вид

,

 

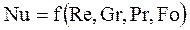· при стационарной теплоотдаче и естественной конвекции

,

 

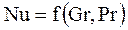· при ламинарном вязкостно-гравитационном течении жидкости

,

 

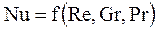· при ламинарном вязкостном течении жидкости

,

 

· при стационарном режиме и турбулентном течении жидкости

.

 

Дифференциальные уравнения, условия однозначности и теоремы подобия позволили получить уравнение подобия стационарного теплообмена в общем виде

,

 

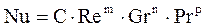где С – безразмерный коэффициент;

m, n, p – безразмерные степенные показатели.

 

Теоремы подобия

 

Первая теорема подобия (теорема Ньютона, 1686г.)