1. Составить параметрические и канонические уравнения прямой, проходящей через точку 
перпендикулярно плоскости 
.
Ответ. 
.
2. Найти точку пересечения прямых 
, 
.
Ответ. 
.
3. Найти расстояние между прямыми
.
Ответ. 1.
4. Доказать, что прямые
и 
пересекаются. Найти точку пересечения. Записать уравнение плоскости, в которой лежат эти прямые.
Ответ. (2,2,1); 
.
5. Через точку 
провести прямую, перпендикулярно Ox и прямой
Ответ. 
.
6. Через точку 
провести прямую, пересекающую прямую 
и параллельную плоскости 
.
Ответ. 
.
7. В уравнениях прямой 
определить параметр 
так, чтобы эта прямая пересекалась с прямой 
и найти точку пересечения.
Ответ. 
, 
.
8. Вычислить расстояние между параллельными прямыми 
и 
.
Ответ. 
.
9. В плоскости yOz найти прямую, проходящую через начало координат и перпендикулярную прямой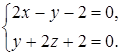 
Ответ. 
.
10. Найти точку пересечения прямой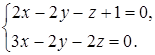 
с плоскостью 
.
Ответ. 
.
11. Найти расстояние между прямыми 
и 
.
Ответ. 7.
12. Через точки 
и 
проведена прямая. Определить точки пересечения этой прямой с координатными плоскостями.
Ответ. (9,–4,0), (3,0,–2), (0,2,–3).
13. Составить канонические уравнения прямой, проходящей через точку 
параллельно прямой 
Ответ. 
.
14. Доказать перпендикулярность прямых:
1) 
и 
2) 
и 
15. Составить параметрические уравнения общего перпендикуляра двух прямых, заданных уравнениями
и 
.
Ответ. 
.
СМЕШАННЫЕ ЗАДАЧИ, ОТНОСЯЩИЕСЯ К УРАВНЕНИЮ
ПЛОСКОСТИ И УРАВНЕНИЯМ ПРЯМОЙ
1. Угол между прямой
и плоскостью  определяется по формуле
 . (4.1)
| 
Рис. 2.22
|
.
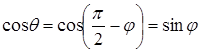2. Условия принадлежности прямой (14) к плоскости (2):
(4.2)
3. Условие параллельности прямой и плоскости:
или 
. (4.3)
4. Условие перпендикулярности прямой и плоскости
или 
. (4.4)
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 4.1. Составить уравнения прямой, проходящей через точку 
перпендикулярно плоскости 
.
Решение. За направляющий вектор 
прямой можно принять нормальный вектор плоскости 
. Искомая прямая будет иметь уравнения 
.
Ответ. .
Задача 4.2. Составить уравнение плоскости, проходящей через точку 
перпендикулярно прямой 
.
Решение. За нормальный вектор плоскости 
можно принять направляющий вектор данной прямой, тогда уравнение запишется в виде (8.1): 
; 
.
Ответ: .
Задача 4.3. Найти проекцию точки 
на прямую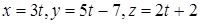 
.
Рис. 2.23
| Решение. Построим вспомогательную плоскость, проходящую через точку перпендикулярно данной прямой, то есть нормальный вектор плоскости имеет вид:  , а уравнение плоскости  (рис. 2.23).
Точка  – точка пересечения построенной
|
плоскости и данной прямой и будет являться искомой проекцией точки P на прямую. Для нахождения точки пересечения решим систему
Из последнего уравнения: при 
, получим 
. Проекция точки на прямую имеет координаты (3,–2,4).
Ответ: (3,–2,4).
Задача 4.4. Найти точку Q, симметричную точке 
относительно плоскости 
.
Решение. Построим прямую, проходящую через точку перпендикулярно плоскости . Уравнения этой прямой имеют вид (8.13): 
. Основанием этого перпендикуляра будет точка пересечения прямой и плоскости. Найдём её, решив систему
Отсюда 
и 
основание перпендикуляра, опущенного из точки P на плоскость. Искомая точка Q лежит на той же прямой, причём 
, но 
, значит 
, отсюда 
. Итак, 
.
Ответ. .
Задача 4.5. Доказать, что прямые
, 
лежат в одной плоскости и составить уравнение этой плоскости.
Решение. Если прямые лежат в одной плоскости (компланарны) и не параллельны, то они пересекаются. Условие пересечения двух прямых имеет вид (8.17). В нашем случае 
, 
, 
, 
, тогда
, 
,
т.е. прямые не параллельны.
Найдём нормальный вектор искомой плоскости. Поскольку он перпендикулярен векторам 
и 
, то его можно представить как векторное произведение:
.
При записи уравнения может быть взята любая из точек 
или 
: 
, 
.
Ответ. 
.
Задача 4.6. Составить параметрические уравнения прямой, которая проходит параллельно плоскостям 
и пересекает прямые
.
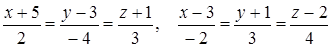Решение. Найдём направляющий вектор искомой прямой. Так как перпендикулярен 
и 
, то за вектор можно принять вектор, коллинеарный векторному произведению 
и 
:
,
то есть 
.
Прямая не является параллельной ни одной координатной оси, поэтому одну из координат точки 
можно задать произвольно, например, 
. Найдём точку 
из условий пересечения искомой прямой с каждой из двух заданных прямых имеет вид (3.9). Выпишем их в нашем случае: сначала условие пересечения прямой с направляющим вектором , и прямой 
, 
, а затем прямой , и прямой 
, 
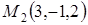. Получим систему уравнений относительно 
и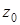 
отсюда 
и 
уравнение искомой прямой примет вид:
.
Ответ. 
Задача 4.7. Составить уравнение прямой, проходящей через точку  и пересекающей прямые  ,  , а также уравнение плоскости проходящей через точку перпендикулярно данным прямым (рис. 2.24).
|
Рис. 2.24
|
Решение. Убедимся, что точка не принадлежит ни одной из данных прямых.
Выясним взаиморасположение данных прямых: 
, 
, 
, 
, 
.
Условие пересечения данных прямых 
не выполнено, прямые скрещивающиеся.
Условия пересечения искомой прямой 
с данными: 
, 
, или 
; 
, 
, или 
.
Решим систему 
, 
, 
.
Пусть 
, полученный при 
.
Искомая прямая: 
.
Плоскость, проходящая через т. перпендикулярно данным прямым: 
, пусть 
, 
.
Ответ. , 
.
