ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
Основные теоретические сведения
В декартовых координатах каждая плоскость определяется уравнением первой степени, и каждое уравнение первой степени определяет плоскость.
1. Уравнение  (2.1)
(2.1)
определяет плоскость, проходящую через точку  и имеющую нормальный вектор
и имеющую нормальный вектор  (рис. 2.13).
(рис. 2.13).
Это уравнение называют уравнением связки плоскостей.
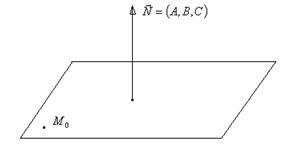 Рис. 2.13
Рис. 2.13
|  Рис. 2.14
Рис. 2.14
|
2. Уравнение  (2.2)
(2.2)
называется общим уравнением плоскости.
3. Уравнение
 (2.3)
(2.3)
является уравнением плоскости «в отрезках», здесь 

 величины отрезков, которые плоскость отсекает на координатных осях (рис. 2.14).
величины отрезков, которые плоскость отсекает на координатных осях (рис. 2.14).
4. Нормальным уравнением плоскости называется уравнение вида
 , (2.4)
, (2.4)
где x, y, z – координаты текущей точки М (x,y,z), принадлежащей плоскости,  – направляющие косинусы нормального вектора плоскости,
– направляющие косинусы нормального вектора плоскости, 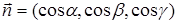 , p – расстояние от плоскости до начала координат.
, p – расстояние от плоскости до начала координат.
Обозначая радиус-вектор текущей точки плоскости через  . Уравнение (2.4) можно записать в векторной форме:
. Уравнение (2.4) можно записать в векторной форме:  .
.
Общее уравнение плоскости (2.2) приводится к нормальному виду (2.4) умножением на нормирующий множитель
 (2.5)
(2.5)
знак m берется противоположным знаку свободного члена уравнения (2.2).
5. Отклонение точки  от плоскости, заданной нормальным уравнением (2.4), вычисляется по формуле
от плоскости, заданной нормальным уравнением (2.4), вычисляется по формуле
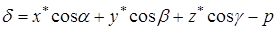 (2.6)
(2.6)
 – расстояние от точки до плоскости, если
– расстояние от точки до плоскости, если 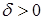 , то
, то 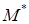 и начало координат находятся по разные стороны плоскости, если
и начало координат находятся по разные стороны плоскости, если  – по одну сторону.
– по одну сторону.
Если дано уравнение плоскости в виде (2.2), то удобнее использовать формулу
 .
.
6. Частные случаи расположения плоскости.

| 
|
Рис. 2.15 Рис. 2.16
Если в общем уравнении плоскости  свободный член D =0, то плоскость проходит через начало координат; если какой-либо из коэффициентов A, B, C обращается в нуль, то плоскость параллельна той оси, название которой отсутствует в уравнении, например, плоскость
свободный член D =0, то плоскость проходит через начало координат; если какой-либо из коэффициентов A, B, C обращается в нуль, то плоскость параллельна той оси, название которой отсутствует в уравнении, например, плоскость 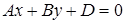 параллельна оси Oz (рис. 2.15), плоскость
параллельна оси Oz (рис. 2.15), плоскость  параллельно оси Оу (рис.2.16), плоскость
параллельно оси Оу (рис.2.16), плоскость  параллельна осям Oy и Oz, то есть параллельна плоскости yОz. Уравнения x =0, y =0, z =0 представляют координатные плоскости zОy, xОz, xОy соответственно.
параллельна осям Oy и Oz, то есть параллельна плоскости yОz. Уравнения x =0, y =0, z =0 представляют координатные плоскости zОy, xОz, xОy соответственно.
7. Угол φ между двумя плоскостями, заданными в общем виде, вычисляется по формуле
 .
.
При 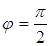 получим условие перпендикулярности плоскостей:
получим условие перпендикулярности плоскостей:
 .
.
Условие параллельности двух плоскостей имеет вид: 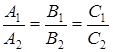 .
.
8. Уравнение вида  (2.7)
(2.7)
где α, β – произвольные числа, не равные нулю одновременно, называется уравнением пучка плоскостей. Это пучок проходит через прямую пересечения плоскостей  и и  (рис. 2.17).
Уравнение плоскости проходящей через три данных точки (рис. 2.17).
Уравнение плоскости проходящей через три данных точки  , ,  , , 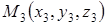 , имеет вид , имеет вид
|  Рис. 2.17
Рис. 2.17
|
 .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 2.1. Составить уравнения плоскостей по следующим данным:
а) плоскость перпендикулярна оси Ох и проходит через  ;
;
б) плоскость проходит через ось Оz и точку  ,
,
в) плоскость параллельна оси Ох и проходит через точки
 и
и  .
.
Решение.
а) Так как искомая плоскость перпендикулярна оси Оx, то её нормальный вектор имеет вид  .Применяя формулу (2.1),запишем искомое уравнение
.Применяя формулу (2.1),запишем искомое уравнение  или
или 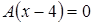 , то есть
, то есть  .
.
б) Так как плоскость проходит через Оz, то в общем, уравнении (2.2) коэффициенты  и
и  , т.е. уравнение имеет вид
, т.е. уравнение имеет вид  . Точка
. Точка  принадлежит плоскости, значит, подстановка координат точки в уравнение плоскости приведёт к тождеству:
принадлежит плоскости, значит, подстановка координат точки в уравнение плоскости приведёт к тождеству:  , отсюда
, отсюда  или
или  , окончательно будем иметь
, окончательно будем иметь  .
.
в) Плоскость параллельна оси Ox, следовательно, имеет вид 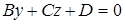 . Подставим координаты точек
. Подставим координаты точек  и
и  , получим систему
, получим систему  решая которую найдем
решая которую найдем 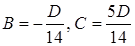 . После подстановки найденных значений В, С в уравнение будем
. После подстановки найденных значений В, С в уравнение будем  или
или  .
.
Ответ: а)  б)
б)  в)
в)  .
.
Задача 2.2. Составить уравнение плоскости, проходящей через точку 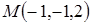 и перпендикулярной плоскостям
и перпендикулярной плоскостям  и
и  .
.
Решение. Нормальные векторы заданных плоскостей имеют вид 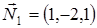 и
и 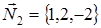 . В силу условия задачи, нормальный вектор
. В силу условия задачи, нормальный вектор  искомой плоскости перпендикулярен векторам
искомой плоскости перпендикулярен векторам  и
и  одновременно, поэтому за вектор
одновременно, поэтому за вектор  примем вектор, равный векторному произведению векторов
примем вектор, равный векторному произведению векторов  и
и  . Таким образом
. Таким образом
 ,
,
следовательно  . Искомое уравнение запишем в виде (2.1)
. Искомое уравнение запишем в виде (2.1)
 или
или  .
.
Ответ. 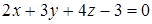 .
.
Задача 2.3. Вычислить объём пирамиды, ограниченной плоскостью  и координатными плоскостями.
и координатными плоскостями.
Решение.
Приведем данное уравнение к уравнению плоскости "в отрезках" (2.3). Для этого перенесем свободный член вправо и разделим обе части уравнения на число
–2, получим  . Таким образом, на осях координат Ox, Oy, Oz данная плоскость отсекает отрезки, равные . Таким образом, на осях координат Ox, Oy, Oz данная плоскость отсекает отрезки, равные 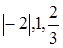 соответственно, считая от начала координат. Пирамида имеет вид, изображенный на рис. 2.18. соответственно, считая от начала координат. Пирамида имеет вид, изображенный на рис. 2.18.
|  Рис. 2.18
Рис. 2.18
|
Пирамида прямая, её объём равен одной шестой от произведения длин этих отрезков, то есть  .
.
Ответ.  .
.
Задача 2.4. Определить, какие из уравнений плоскостей являются нормальными:
а)  ,
,
б)  ,
,
в) 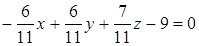 .
.
Решение.
Для уравнение плоскости в нормальной форме (2.4),
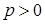 и
и 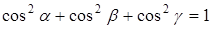 .
.
Проверим выполнение этих условий:
а) так как р <0, то уравнение не является нормальным;
б) имеем р >0, 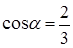 ,
,  ,
, 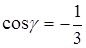 , но тогда
, но тогда 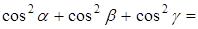
 , следовательно, уравнение не является нормальным.
, следовательно, уравнение не является нормальным.
в) здесь р >0, 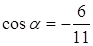 ,
, 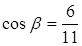 ,
,  , вычисляя
, вычисляя 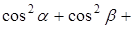
 . Уравнение является нормальным.
. Уравнение является нормальным.
Задача 2.5. Определить расстояние от плоскости  до:
до:
а) начала координат,
б) точки  ,
,
в) точки 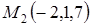 .
.
Решение.
Приведем уравнение данной плоскости к нормальному виду (2.4).
Для этого умножим обе части уравнения на нормирующий множитель (2.5), знак которого выбираем отрицательным. Вычислим
 .
.
Уравнение примет нормальную форму  . При этом p =2, а p – расстояние от плоскости до начала координат по определению.
. При этом p =2, а p – расстояние от плоскости до начала координат по определению.
а) Расстояние от плоскости до начала координат равно 2.
б) Определим отклонение d по формуле (2.6), где точка 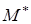 имеет координаты (7,0,0). Тогда
имеет координаты (7,0,0). Тогда 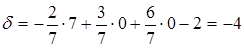 , следовательно, расстояние от точки
, следовательно, расстояние от точки  до плоскости равно 4, точка
до плоскости равно 4, точка  и начало координат находятся по одну сторону плоскости (d <0). То же самое по формуле (2.7):
и начало координат находятся по одну сторону плоскости (d <0). То же самое по формуле (2.7):  .
.
в) Определим расстояние от точки  до плоскости:
до плоскости: 
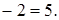 Точка
Точка  и начало координат расположены по разные стороны (d>0).
и начало координат расположены по разные стороны (d>0).
Самостоятельно найти это же расстояние по формуле (2.7).
Задача 2.6. Доказать, что плоскость  пересекает отрезок, ограниченный точками
пересекает отрезок, ограниченный точками  и
и 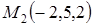 .
.
Решение.
Приведём уравнение  к нормальному виду (2.4). При этом
к нормальному виду (2.4). При этом 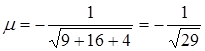 и уравнение примет вид
и уравнение примет вид

Вычислим отклонения  ,
,  точек
точек  и
и 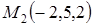 от плоскости
от плоскости

по формуле (2.6), получим
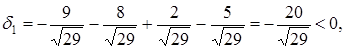

т.е. точки  и
и  лежат по разные стороны от плоскости, следовательно, плоскость пересекает отрезок
лежат по разные стороны от плоскости, следовательно, плоскость пересекает отрезок 
Задача 2.7. Вычислить расстояние между плоскостями  и
и 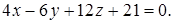
Решение. Способ 1. Так как нормальные векторы  ;
;  плоскостей имеют пропорциональные координаты
плоскостей имеют пропорциональные координаты
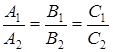 ,
,
то плоскости параллельны. Чтобы найти расстояние между ними, приведём уравнения плоскостей к нормальному виду, получим  и
и 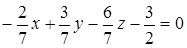 . Так как векторы
. Так как векторы  и
и  противоположно направлены, то эти плоскости расположены по разные стороны от начала координат на расстоянии 2 и
противоположно направлены, то эти плоскости расположены по разные стороны от начала координат на расстоянии 2 и 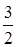 соответственно. Следовательно, расстояние между ними равно
соответственно. Следовательно, расстояние между ними равно 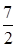 .
.
Способ 2. Выберем на плоскости  произвольную точку М, например точку пересечения с осью Oz, тогда
произвольную точку М, например точку пересечения с осью Oz, тогда  (нашли из уравнения плоскости).
(нашли из уравнения плоскости).
Теперь задача сводится к нахождению расстояния от точки М (0,0,  ) до плоскости
) до плоскости 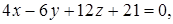
 .
.
Ответ. 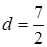 .
.
Задача 2.8. Вычислить расстояние от точки Р (–1,1,–2) до плоскости, проходящей через три точки  ,
,  и
и  .
.
Решение.
Составим уравнение плоскости, проходящей через три точки:


Вычисляя определитель обычным образом (лучше всего разложением по первой строке), получим 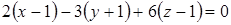 или
или
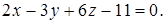
Приведём это уравнение к нормальному виду. Умножив на нормирующий множитель  , будем иметь
, будем иметь  . Определим отклонение
. Определим отклонение  по формуле (2.6)
по формуле (2.6)  , следовательно, расстояние от точки Р до плоскости равно 4.
, следовательно, расстояние от точки Р до плоскости равно 4.
Ответ.  .
.
Задача 2.9. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей  перпендикулярно плоскости
перпендикулярно плоскости 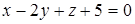 .
.
Решение. Используя формулу (2.7) составим уравнение пучка плоскостей:  . Раскроем скобки, приведём подобные члены, получим
. Раскроем скобки, приведём подобные члены, получим 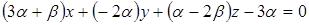 . Это уравнение определяет любую плоскость проходящую через прямую пересечения плоскостей
. Это уравнение определяет любую плоскость проходящую через прямую пересечения плоскостей 
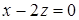 . Нормальный вектор имеет вид
. Нормальный вектор имеет вид  .
.
Согласно условно, плоскость  с нормальным вектором
с нормальным вектором  и искомая плоскость с нормальным вектором
и искомая плоскость с нормальным вектором  перпендикулярны, значит по формуле (2.9)
перпендикулярны, значит по формуле (2.9)  . Получим уравнение
. Получим уравнение 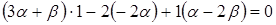 или
или  , т.е.
, т.е.  . Полученное соотношение подставим в уравнение пучка
. Полученное соотношение подставим в уравнение пучка 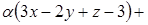
 . Окончательно будем иметь
. Окончательно будем иметь 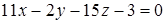 .
.
Ответ. 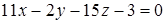 .
.
Задача 2.10. Определить, принадлежит ли плоскость  пучку плоскостей
пучку плоскостей  .
.
Решение. Преобразуем уравнение пучка плоскостей к виду

и определим, не будет ли противоречива система, полученная при сравнении коэффициентов плоскости пучка и плоскости  . Система имеет вид:
. Система имеет вид:
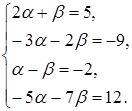
Решим ее:  , подставам в следующее уравнение, получим
, подставам в следующее уравнение, получим 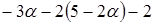 или
или  , подставляя в третье уравнение, будем иметь
, подставляя в третье уравнение, будем иметь  или
или  . Из четвертого уравнения получим
. Из четвертого уравнения получим 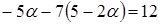 или
или  . Таким образом, система противоречива, то есть плоскость не принадлежит пучку плоскостей.
. Таким образом, система противоречива, то есть плоскость не принадлежит пучку плоскостей.
Задачи для самостоятельного решения
1.Составить уравнения плоскостей, параллельных координатным плоскостям и проходящим через точку  .
.
Ответ:  .
.
2. Составить уравнение плоскости, проходящей через линию пересечения плоскостей 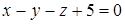 и
и 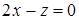 и параллельной вектору
и параллельной вектору  .
.
Ответ: 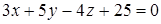 .
.
3. Вычислить расстояние от точки  до плоскости, проходящей через точки
до плоскости, проходящей через точки  .
.
Ответ: d =9.
4. Даны плоскости 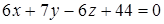 и
и  . Какая из них ближе к началу координат?
. Какая из них ближе к началу координат?
Ответ: 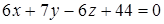 .
.
5. Две грани куба лежат соответственно на плоскостях  и
и 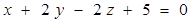 . Вычислить объем данного куба.
. Вычислить объем данного куба.
Ответ: 8 куб.ед.
6. Доказать, что параллелепипед, три непараллельные грани которого лежат в плоскостях
 ,
,
 ,
,

является прямоугольным.
7. На оси ординат найти точку, отстоящую от плоскости 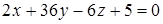 на расстоянии трёх единиц.
на расстоянии трёх единиц.
Ответ: 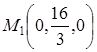 ,
,  .
.
8. Составить уравнение плоскости, проходящей через точку  и отсекающей равные отрезки на осях координат.
и отсекающей равные отрезки на осях координат.
Ответ:  .
.
9. Из точки  на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.
на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.
Ответ:  .
.
10. Найти уравнение плоскости, точки которой одинаково удалены от точек  и
и  .
.
Ответ:  .
.
ПРЯМАЯ В ПРОСТРАНСТВЕ
Основные теоретические сведения
1. Общее уравнение прямой:
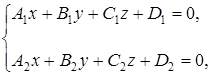 (3.1)
(3.1)
определяется как линия пересечения двух плоскостей, при условии, что они не параллельны.
Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим этой прямой  . Если известна одна точка
. Если известна одна точка  , принадлежащая прямой, то прямая может быть задана каноническими уравнениями:
, принадлежащая прямой, то прямая может быть задана каноническими уравнениями:  .
.
2.  . (3.2)
. (3.2)
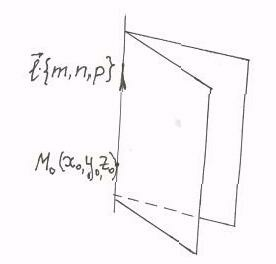 Рис. 2.19
Рис. 2.19
|
3. Параметрическими уравнениями прямой, проходящей через точку  в направлении вектора в направлении вектора 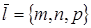 , называются уравнения вида: , называются уравнения вида:
 (3.3) (3.3)
|
Здесь  произвольно изменяющийся параметр. При изменении
произвольно изменяющийся параметр. При изменении  величины
величины  меняются так, что точка
меняются так, что точка  движется по данной прямой.
движется по данной прямой.
4. Канонические уравнения прямой, проходящей через две данные точки  и
и  имеет вид
имеет вид
 . (3.4)
. (3.4)
Параметрические уравнения прямой, проходящей через две данные точки
 (3.5)
(3.5)
Если в системе (3.5) t меняется на отрезке  , то (3.5) определяет отрезок прямой
, то (3.5) определяет отрезок прямой  причем параметру
причем параметру  соответствует точка
соответствует точка  , параметру
, параметру  – точка
– точка  .
.
5. Угол  между двумя прямыми, заданными своими каноническими или параметрическими уравнениями, вычисляются по формуле
между двумя прямыми, заданными своими каноническими или параметрическими уравнениями, вычисляются по формуле
 . (3.6)
. (3.6)
6. Условие параллельности прямых
 (3.7)
(3.7)
Условие перпендикулярности прямых
 (3.8)
(3.8)
следует из условия перпендикулярности направляющих векторов.
7. Условие пересечения прямых (условие компланарности):
 Рис. 2.20
Рис. 2.20
|  (3.9)
Это условие (3.9) – условие компланарности прямых (рис. 2.20). Если оно не выполняется и прямые не параллельны, то данные прямые называются скрещивающимися (лежат в параллельных плоскостях). (3.9)
Это условие (3.9) – условие компланарности прямых (рис. 2.20). Если оно не выполняется и прямые не параллельны, то данные прямые называются скрещивающимися (лежат в параллельных плоскостях).
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 3.1. Составить уравнение прямой, образованной пересечением плоскости  с плоскостью, проходящей через ось Ох и точку
с плоскостью, проходящей через ось Ох и точку  .
.
Решение. Составим уравнение плоскости, проходящей через ось Ох и точку  . Нормальный вектор этой плоскости имеет вид
. Нормальный вектор этой плоскости имеет вид  . Используем уравнение (3.1), получим
. Используем уравнение (3.1), получим  или
или  . Но так как плоскость проходит через начало координат, то
. Но так как плоскость проходит через начало координат, то  , следовательно,
, следовательно,  . Тогда
. Тогда  или
или  уравнение искомой плоскости. Прямую запишем в общем виде (3.2)
уравнение искомой плоскости. Прямую запишем в общем виде (3.2)

Ответ. 
Задача 3.2. Через точки  и
и  проведена прямая. Определить точки пересечения этой прямой с координатными плоскостями.
проведена прямая. Определить точки пересечения этой прямой с координатными плоскостями.
Решение. Запишем уравнение прямой, проходящей через две точки в параметрической форме (3.5), получим

Найдём пересечение этой прямой с координатной плоскостью xOy, которая имеет уравнение  для этого решим совместно уравнения прямой и плоскости
для этого решим совместно уравнения прямой и плоскости

Отсюда  , следовательно,
, следовательно,  , тогда
, тогда
 ,
,
т.е. точка (9;-4;0) является точкой пересечения прямой и плоскости xОy.
Решая две системы
 и
и 
Найдём точки пересечения прямой с плоскостями yОz и zОy –точки (0,2,-3) и (3,0,–2) соответственно.
Ответ: (9;–4;0); (0;2;–3); (3;0;–2).
Задача 3.3. Составить канонические и параметрические уравнения прямой
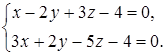
Решение. Найдём направляющий вектор данной прямой. Его можно считать параллельным векторному произведению нормальных векторов  , где
, где  и
и  составляющих плоскостей. Итак,
составляющих плоскостей. Итак,
 .
.
За направляющий вектор прямой возьмём  ,
, 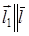
Выберем точку 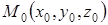 , принадлежащую прямой, так как прямая не параллельна ни одной из координатных плоскостей, то в системе
, принадлежащую прямой, так как прямая не параллельна ни одной из координатных плоскостей, то в системе

можно одну из координат 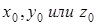 задать произвольно, например, положить
задать произвольно, например, положить 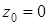 , что соответствует пересечению прямой с плоскостью xОy. Тогда система примет вид:
, что соответствует пересечению прямой с плоскостью xОy. Тогда система примет вид:

Сложив оба уравнения, получим 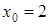 , затем найдём
, затем найдём  . Таким образом, одна из точек прямой
. Таким образом, одна из точек прямой  имеет координаты (2,–1,0). Составим канонические уравнения прямой:
имеет координаты (2,–1,0). Составим канонические уравнения прямой: 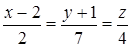 . Для записи прямой в параметрической форме приравняем каждую дробь параметру t и разрешим относительно переменных x, y, z
. Для записи прямой в параметрической форме приравняем каждую дробь параметру t и разрешим относительно переменных x, y, z
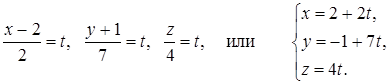
Ответ: 
Задача 3.4. Найти угол между прямыми; лежащими в одной плоскости:
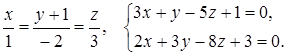
Решение. Направляющий вектор первой прямой имеет вид 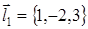 . Найдём направляющий вектор второй прямой
. Найдём направляющий вектор второй прямой  . Сначала вычислим векторное произведение нормальных векторов плоскостей:
. Сначала вычислим векторное произведение нормальных векторов плоскостей:
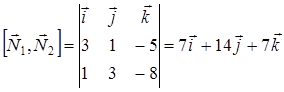 .
.
За  примем вектор
примем вектор 
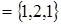 ,
,  . Найдём угол между прямыми по формуле (3.6)
. Найдём угол между прямыми по формуле (3.6)
 ,
,
то есть  , прямые перпендикулярны.
, прямые перпендикулярны.
Ответ:  .
.
Задача 3.5. Доказать, что прямые
 и
и 
пересекаются.
Решение. Условие пересечения двух прямых имеет вид (3.9). В нашем случае  ,
,  ,
,  ,
,  . Зная точки М 1 и М 2 найдем вектор
. Зная точки М 1 и М 2 найдем вектор 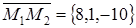 .
.
Составим определитель по формуле (3.9) и убедимся, что он равен нулю, т.е. вектора пересекаются
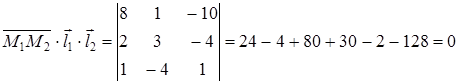 .
.
Ответ. Прямые пересекаются.
Задача 3.6. Составить уравнение прямой, которая проходит через точку  перпендикулярно к вектору
перпендикулярно к вектору  и пересекает прямую
и пересекает прямую
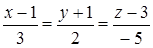 .
.
Решение. Для того, чтобы составить канонические уравнения прямой, надо найти направляющий вектор  . Предположим, что координата
. Предположим, что координата 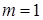 . Тогда найдем вектор
. Тогда найдем вектор  , удовлетворяющий двум условиям: во-первых,
, удовлетворяющий двум условиям: во-первых,  и
и 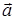 перпендикулярны, т.е. скалярное произведение
перпендикулярны, т.е. скалярное произведение  ; во-вторых, должно выполняться условие пересечения двух прямых (3.9), причём
; во-вторых, должно выполняться условие пересечения двух прямых (3.9), причём  ,
,  ,
,  ,
, 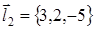 .
.
Запишем эти два условия:
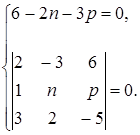 или
или 
Решаем последнюю систему, получим  ,
, 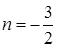 таким образом,
таким образом,  . За направляющий вектор примем
. За направляющий вектор примем  . Искомое уравнение примет вид:
. Искомое уравнение примет вид:  .
.
Ответ. 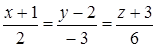 .
.
Задача 3.7. Из начала координат опустить перпендикуляр на прямую
 .
.
Решение. Составим уравнение вспомогательной плоскости, проходящей через начало координат и перпендикулярной данной прямой. Направляющий вектор прямой  служит нормальным вектором этой плоскости, получим
служит нормальным вектором этой плоскости, получим  . Найдём точку пересечения данной прямой и плоскости
. Найдём точку пересечения данной прямой и плоскости  . Для этого удобно уравнения прямой записать в параметрической форме и решить уравнения прямой и плоскости совместно
. Для этого удобно уравнения прямой записать в параметрической форме и решить уравнения прямой и плоскости совместно

Отсюда 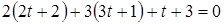 ,
,  , т.е.
, т.е. 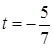 . Тогда точка пересечения M имеет координаты
. Тогда точка пересечения M имеет координаты  (
(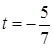 подставили в параметрическое уравнение прямой).
подставили в параметрическое уравнение прямой).
Направляющий вектор искомой прямой параллелен радиус-вектору точки M, т.е. вектору с координатами  . За . За  удобно принять вектор удобно принять вектор  , т.е. , т.е.  . Искомая прямая примет вид: . Искомая прямая примет вид:  (рис. 2.21).
Ответ. (рис. 2.21).
Ответ.  . .
|
 Рис. 2.21
Рис. 2.21
|
Задача 3.8. Определить кратчайшее расстояние между скрещивающимися прямыми:
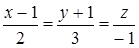 ,
,  .
.
Решение. На скрещивающихся прямых можно построить параллелепипед с рёбрами 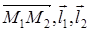 . Кратчайшее расстояние между прямыми совпадает с высотой этого параллелепипеда, площадь основания которого равна
. Кратчайшее расстояние между прямыми совпадает с высотой этого параллелепипеда, площадь основания которого равна  . Поскольку объём параллелепипеда, с одной стороны, равен
. Поскольку объём параллелепипеда, с одной стороны, равен  , а с другой стороны,
, а с другой стороны, 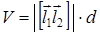 , т.е.
, т.е.  .
.
В нашем случае 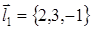 ,
,  ,
,  ,
,  , следовательно,
, следовательно,  . Тогда
. Тогда
 ,
,
 .
.
Смешанное произведение
 ,
,
т.е.  . Таким образом, расстояние
. Таким образом, расстояние  .
.
Ответ.  .
.






