Прямая на плоскости
Основные теоретические сведения
1. Общее уравнение прямой на плоскости в декартовой системе координат
 , (1.1)
, (1.1)
А и В одновременно не равны нулю. Прямая перпендикулярна нормальному вектору  (рис. 2.1).
(рис. 2.1).
2. Частные случаи для (1.1):
 ,
,  (рис. 2.2).
(рис. 2.2).
 Рис. 2.1
Рис. 2.1
|
 Рис. 2.2
Рис. 2.2
|
 ,
,  (рис. 2.3).
(рис. 2.3).
 Рис. 2.3
Рис. 2.3
|  Рис. 2.4
Рис. 2.4
|
 ,
,  (рис. 2.4).
(рис. 2.4).
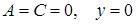 – прямая совпадает с осью Ох (абсцисс).
– прямая совпадает с осью Ох (абсцисс).
 – прямая совпадает с осью Оу (ординат).
– прямая совпадает с осью Оу (ординат).
3. Уравнение прямой с угловым коэффициентом
 (1.2)
(1.2)
 ,
,  – наименьший угол между положительным направлением оси Ох и прямой; b – отрезок, отсекаемый прямой от оси ординат (рис. 2.1).
– наименьший угол между положительным направлением оси Ох и прямой; b – отрезок, отсекаемый прямой от оси ординат (рис. 2.1).
Для прямой (1.1) 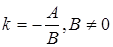
4. Уравнение прямой в отрезках
 , (1.3)
, (1.3)
а и b – абсцисса и ордината точек пересечения с осями Ох и Оу, т.е длины отрезков, отсекаемых прямой от координатных осей с учетом знаков (рис. 2.5)
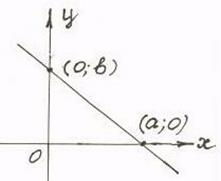 Рис. 2.5
Рис. 2.5
|  Рис. 2.6
Рис. 2.6
|
5. Уравнение прямой, проходящей через данную точку  с данным угловым коэффициентом
с данным угловым коэффициентом
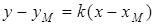 . (1.4)
. (1.4)
Пучком прямых на плоскости называется вся совокупность прямых, проходящих через данную точку (центр пучка), все прямые отличаются значениями k (рис. 2.6).
6. Уравнение прямой, проходящей через две данные точки с координатами  и
и  (рис. 2.7)
(рис. 2.7)
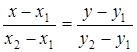 . (1.5)
. (1.5)
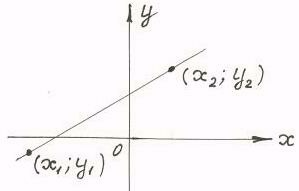
|
Рис. 2.7
Если прямая параллельна оси Ох (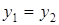 ) или оси Оу
) или оси Оу  , то уравнение (1.5) примет вид
, то уравнение (1.5) примет вид  или
или 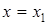 .
.
Если прямая проходит через точку  или
или  параллельно направляющему вектору
параллельно направляющему вектору  , то уравнение примет вид
, то уравнение примет вид
 . (1.6)
. (1.6)
Уравнение (1.6) называется каноническим уравнением прямой.
7. Нормальное уравнение прямой
 , (1.7)
, (1.7)
где p – расстояние от начала координат до прямой, 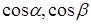 – направляющие косинусы нормального вектора
– направляющие косинусы нормального вектора  .
.
Уравнение (1.1) приводиться к виду (1.7) путем умножения на нормирующий множитель 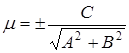 , знак выбирается обратным знаку свободного члена С в уравнении (1.1), т.е
, знак выбирается обратным знаку свободного члена С в уравнении (1.1), т.е 
 (sgn – сокращение от латинского signum – знак).
(sgn – сокращение от латинского signum – знак).
8. Расстояние от точки 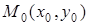 до прямой
до прямой 
 . (1.8)
. (1.8)
9. Угол между прямыми, заданными уравнениями вида (1.2):
 , (1.9)
, (1.9)
 .
.
За  принят угловой коэффициент той из прямых, которая, вращаясь вокруг точки пересечения прямых против часовой стрелки «заметает» угол
принят угловой коэффициент той из прямых, которая, вращаясь вокруг точки пересечения прямых против часовой стрелки «заметает» угол  (рис. 2.8).
(рис. 2.8).

|
Рис. 2.8
10. Взаимное расположение прямых на плоскости:
- прямые пересекаются  или
или  ;
;
- если пресекаются под прямым углом, то из формулы (1.9), следует

- прямые параллельны  при
при 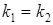 ;
;
- прямые совпадают 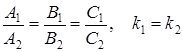 .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 2.1. Какая из точек  лежит на прямой 2 x – y +4=0.
лежит на прямой 2 x – y +4=0.
Решение: Подставим координаты точек в уравнение прямой:
т. 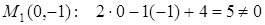 , точка не принадлежит прямой;
, точка не принадлежит прямой;
т.  т.
т.  принадлежит прямой;
принадлежит прямой;
т.  , т.
, т.  принадлежит прямой.
принадлежит прямой.
Задача 2.2. Вычислить угол между прямыми 6 x– 2 y +5=0 и 4 x +2 y –7=0, и найти точку пересечения 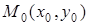 .
.
Решение: Запишем уравнения прямых с угловым коэффициентом: 2 y =6 x +5, 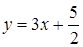 ,
,  , 4 x +2 y –7=0,
, 4 x +2 y –7=0,  ,
, 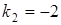 ,
,
 .
.
Найдем точку пресечения прямых:

Сложим уравнения системы:  , 10 x =2,
, 10 x =2,  .
.
Из 2-го уравнения системы:  .
.
Координаты точки пересечения 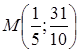 .
.
Ответ. 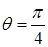 ,
, 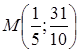 .
.
Задача 2.3. Составить уравнение прямой, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой  .
.
Решение: Используем уравнение пучка прямых (1.4):
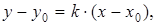
где  .
.
Из условия перпендикулярности (пункт 10):

Запишем данную прямую в виде (1.2)
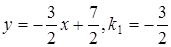 , тогда
, тогда  ;
;
 или
или  .
.
Ответ.  .
.
Задача 2.4. Дана прямая  . Через точку
. Через точку  провести прямую под углом
провести прямую под углом  к данной.
к данной.
Решение:  – уравнение данной прямой. Найдем ее угловой коэффициент
– уравнение данной прямой. Найдем ее угловой коэффициент  (из пункта 3),
(из пункта 3),  (рис. 2.9).
(рис. 2.9).
 Рис. 2.9
Рис. 2.9
|
 ;
;
 или
или  ;
;
 , тогда
, тогда  ;
;  ;
;
 или
или  .
.
Ответ.  ,
,  .
.
Задача 2.5. Дан треугольник с вершинами  . Составить уравнение его сторон и найти длину высоты
. Составить уравнение его сторон и найти длину высоты  (рис. 2.10).
(рис. 2.10).
 Рис. 2.10
Рис. 2.10
|
Решение: Уравнение стороны АВ:
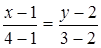 или
или  .
.
Уравнение стороны ВС имеет вид  , т.к. ординаты точек В и С равны. Уравнение стороны АС имеет вид
, т.к. ординаты точек В и С равны. Уравнение стороны АС имеет вид  , т.к. абсциссы точек равны. Длину высоты
, т.к. абсциссы точек равны. Длину высоты  найдем как расстояние т. С до прямой АВ:
найдем как расстояние т. С до прямой АВ:
 .
.
Задача 2.6. Какие из уравнений являются нормальными в декартовой системе координат?
1.  . 4.
. 4.  .
.
2.  . 5.
. 5.  .
.
3. 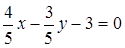 . 6.
. 6. 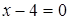 .
.
Решение: Нормальные уравнения 3, 5 и 6, так как для них  и
и  .
.
Задача 2.7. Найти точку, равноудаленную от трех данных точек.
Решение: Такой точкой будет пересечение серединных перпендикуляров.
 Рис. 2.11
Рис. 2.11
|
Уравнение прямой PQ:


 .
.
Точка М – середина отрезка PQ:
 ,
,  .
.
Прямая ОМ – серединный перпендикуляр отрезка PQ:
 ;
;
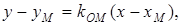
 ,
,
 .
.
Уравнение прямой RQ:  или
или  .
.
Точка N – середина отрезка RQ:
 ,
,  .
.
Уравнение прямой NO:  .
.


или
 .
.
Найдем точку пересечения прямых ON и OM:

Вычтем из второго первое уравнение: 
 . Из второго уравнения
. Из второго уравнения  тогда
тогда 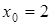 . Равноудаленная точка имеет координаты (2;2).
. Равноудаленная точка имеет координаты (2;2).
Ответ. (2;2).






