Рассмотрим те же самые кривые, изменив параметризацию и масштаб
Здесь появился масштабный фактор 
и изменились параметры. Новые параметры 
и 
— это длина траектории и интервал вдоль мировой линии. В правильности расстановки коэффициентов легко убедиться из соображений размерности: аргументы тригонометрических и гиперболических функций должны быть безразмерными, а координаты (включая время) имеют размерность длины (или времени, что то же самое). Мы можем обратить в единицу, если в качестве единицы измерения длины и времени выбрать 
.
Запишем в обоих случаях радиус-векторы и первые две производные от них по
параметрам и
Геометрический смысл вектора 
— единичная касательная, а вектора 
— вектор кривизны, его длина — обратная величина к радиусу кривизны ( всегда перпендикулярен , т.е. 
). Если двигаться по окружности так, чтобы параметр задавал время, то — скорость, а — ускорение. (Это движение по окружности мы рассматриваем как нерелятивистское!).
Физический смысл вектора 
— релятивистская («четырёхмерная») скорость (тоже единичная касательная, но уже в смысле метрики Минковского), а вектора 
— релятивистское («четырёхмерное») ускорение (аналог вектора кривизны, тоже всегда перпендикулярно , но уже в смысле метрики Минковского, т.е. 
).
При 
имеем 
, а 
. При этом все три окружности, на которых лежат концы векторов 
сливаются в одну единичную окружность, сливаются в одну единичную гиперболу и две гиперболы, на которых лежат концы векторов 
и .
Домножив векторы скорости и на массу («массу покоя») 
мы получим вектор импульса 
и вектор релятивистского импульса 
. Компонентами релятивистского импульса являются энергия 
и обычный механический импульс
Импульс оказался пропорциональным времени! Это означает, что движение происходит под действием постоянной силы
Таким образом, гиперболическое движение является релятивистским аналогом равноускоренного движения под действием постоянной силы (чуть ниже мы углубим эту аналогию). Такое движение имеет место, например, в линейном ускорителе, где заряженная частица разгоняется вдоль прямой под действием постоянной силы создаваемой однородным электрическим полем.
На рисунке изображены мировые линии равноускоренной частицы согласно классической механике (синяя парабола) и согласно СТО (красная гипербола). На классической мировой линии обозначены точки, когда частица достигает скорости света и проведены касательные в этих точках. Видно, что кривые начинают заметно расходиться только на скоростях сравнимых со скоростью света.
Домножив векторы ускорения и на массу («массу покоя») мы получим вектор силы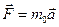 
и вектор релятивистской силы 
(2-й закон Ньютона).
Движущийся наблюдатель
Как эти два движения (классическое круговое и релятивистское гиперболическое) выглядят с точки зрения наблюдателя который эти движения совершает?
Если наблюдатель катается с единичной скоростью по кругу сидя на карусели, то на него всё время действует сила направленная к центру круга, т.е. перпендикулярно скорости, поэтому если наблюдатель всё время сидит лицом по ходу движения, то все моменты времени для него эквивалентны: скорость вперёд, а сила налево, абсолютные величины те же самые, а поворот векторов компенсируется поворотом самого наблюдателя. Для такого наблюдателя удобно в каждый момент времени брать новую систему отсчёта, повёрнутую так, чтобы наблюдатель оставался на оси 
(положительной полуоси). Тогда в любой момент времени в соответствующей системе отсчёта
Если наблюдатель ускоряется под действием постоянной силы вдоль прямой, то удобно в каждый момент времени брать новую систему отсчёта, такую, что чтобы наблюдатель оставался на оси 
(положительной полуоси), т.е. (в силу свойств гиперболы) имел нулевую скорость. Тогда в любой момент времени в соответствующей системе отсчёта
Напомним, что релятивистская скорость с компонентами 
как раз соответствует нулевой обычной скорости, т.к. ненулевая компонента — временная (во времени нельзя остановиться).
Таким образом, для нашего равноускоренного наблюдателя все моменты времени тоже оказались равноценны, а значит для него гиперболическое движение — равноускоренное.
