Алгебраическая точка зрения
Итак, у нас есть замечательная функция экспонента, производная от которой совпадает с самой экспонентой.
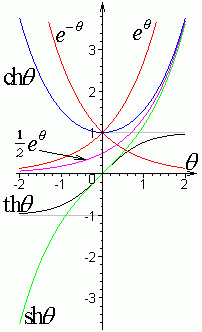
Чётная часть экспоненты — гиперболический косинус:
Нечётная — гиперболический синус, их отношение — гиперболический тангенс:
При больших значениях аргумента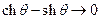 
, 
, 
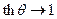. (см. рисунок).
Легко убедиться, что
Также легко проверить основное тождество гиперболической тригонометрии
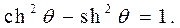
Аналогично могут быть введены и обычные тригонометрические функции:
Механическая (нерелятивистская) точка зрения
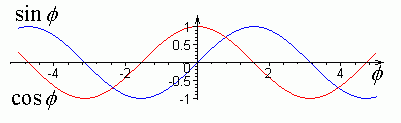Тригонометрические функции (косинус и синус) можно представить как чётное и нечётное решение дифференциального уравнения
Если рассматривать 
как время, то это — уравнение движения (нерелятивистского движения, описываемого обычным 2-м законом Ньютона) гармонического осциллятора (грузика на пружинке) с единичной массой и единичной жёсткостью. В этом случае при отклонении грузика от устойчивого положения равновесия (от нуля) на него действует сила равная величине отклонения и направленная в сторону положения равновесия. Эта возвращающая сила заставляет грузик колебаться около положения равновесия.
Аналогично гиперболические функции (гиперболические косинус и синус) можно представить как чётное и нечётное решения дифференциального уравнения
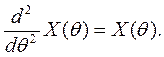
Если рассматривать 
как время, то это — уравнение движения (нерелятивистского движения, описываемого обычным 2-м законом Ньютона) «неправильного» гармонического осциллятора с единичной массой и единичной жёсткостью. В этом случае при отклонении грузика от неустойчивого положения равновесия (от нуля) на него действует сила равная величине отклонения и направленная в сторону отклонения. Эта отталкивающая сила заставляет грузик экспоненциально увеличивать отклонение от положения равновесия.
В обоих случаях в силу линейности дифференциальных уравнений мы можем рассматривать 
и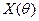 
как векторы в двухмерном пространстве (увеличение размерности больше 2 не даст ничего нового, т.к. движение всё равно будет проходить в одной плоскости). В обоих случаях сила направлена вдоль линии проходящей через начало координат, т.е. момент силы равен нулю, и момент импульса сохраняется. Закон сохранения момента импульса для точки в центральном поле даёт закон равных площадей (аналог 2-го закона Кеплера).
Из двух параметрических кривых
(единичная окружность, поскольку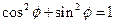 
) и
(правая ветвь единичной гиперболы, поскольку 
и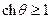 
) могут быть получены общие решения уравнений и (в силу их линейности) с помощью растяжений (сжатий) по 
и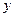 
, поворота системы координат и сдвига по времени. Что такое семейство решений общее, легко убедиться подсчитав параметры.
Закон равных площадей говорит, что приращение площади, заметаемой радиус-вектором пропорционально приращению времени. В случае единичной окружности и единичной гиперболы легко видеть, что площадь между осью , радиус-вектором и дугой кривой равна половине аргумента.
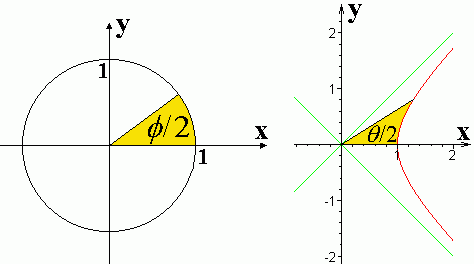
Это следует из рассмотрения бесконечномалого приращения площади в нулевой момент времени (ниже мы ещё к этому вернёмся и докажем подробнее) 
Когда круговой угол пробегает значения 
точка бесконечное число раз пробегает окружность против часовой стрелки. Когда гиперболический угол 
пробегает значения точка один раз снизу вверх пробегает по ветви гиперболы.
