За допомогою графа моделюються будь-які схеми, в яких виділяються більш прості частини (вершини) і зв’язки між ними (ребра). Не дивно, що графи зустрічаються у дослідженнях із соціології, психології, економіки, теорії ігор, логіки, програмування електро- та радіотехніки та ін. Деякі логічні задачі зручно розв’язувати за допомогою побудови графів. Застосовуючи граф до розв’язання логічної задачі, як правило, його вершинам і ребрам надають певний зміст.
õ Приклади задач
1. Представити заданий граф матрицею суміжності.
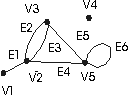
Рис.1. Неорієнтований граф
Розв ’ язок: граф можна представити матрицею суміжності. Рядки й стовпці матриці відповідатимуть вершинам графа, її (i,j) елемент дорівнює кількості кратних ребер, що зв’язують вершини vi, vj. Маємо таку матрицю суміжності:
| v1 | v2 | v3 | v4 | v5 | |
| v1 | |||||
| v2 | |||||
| v3 | |||||
| v4 | |||||
| v5 |
2. Записати матрицю інцидентності для вказаного вище графа (рис.1).
Розв ’ язок: інцидентність — відношення між вершинами й ребрами. Для неорієнтованого графа елементи цієї матриці визначаються за таким правилом: (i,j) елемент дорівнює 1, якщо viінцидентна ребру ei, і дорівнює 0, якщо вони не інцидентні. У випадку орграфа дорівнює 1, якщо vi —початкова вершина ребра, і дорівнює 1, якщо vi — кінцева вершина. Маємо таку матрицю інцидентності для графа на рис. 1.
| e1 | e2 | e3 | e4 | e5 | e6 | |
| v1 | ||||||
| v2 | ||||||
| v3 | ||||||
| v4 | ||||||
| v5 |
3. У місті проводилась нарада лікарів. Від кожної поліклініки на нараду було запрошено по п’ять лікарів. Виявилось, що кожний із запрошених працює у двох поліклініках, тому на нараді представляє обидві поліклініки. Крім того, для будь-яких двох поліклінік міста серед учасників наради знайдеться лікар, який у них працює. Скільки у місті поліклінік? Скільки лікарів брали участь у нараді?
Розв ’ язок: побудуємо граф, домовившись зображати точкою (вершина графа) поліклініку, а запрошеного від неї лікаря — ребром графа, що виходить із цієї точки. Від поліклініки А запрошено 5 лікарів. Отже, із вершини А графа виходить 5 ребер. Але за умовою кожний із запрошених працює у двох поліклініках і представляє на нараді обидві, тому у кінці кожного з проведених із вершини А ребер потрібно поставити по вершині графа. Крім того, кожні дві вершини повинні бути з’єднані ребром. Граф має 6 вершин, 15 ребер, тобто 6 поліклінік, 15 лікарів.
4. Запишіть формулу, що відповідає контактній схемі на рис. 2.

Рис. 2. Двополюсна контактна схема
Контактну схему можна повністю зобразити графом, ребра якого відповідають ключам, а вершини — точкам їх з’єднання. При зображенні контактних схем графами приймаються деякі специфічні умови й спрощення. Зазвичай змінні позначаються у розривах ліній, котрі зображують ребра. При цьому ребрами вважаються лише такі лінії, які позначені змінною або її запереченням. Інші лінії, що не є ребрами графа, можуть показувати входи та виходи схеми, зв¢язки з іншими схемами.
Задача аналізу контактної схеми полягає у побудові відповідної їй булевої функції. Для паралельно-послідовних схем ця задача розв’язується на основі того, що паралельне з’єднання контактів відповідає диз’юнкції, а послідовне — кон’юнкції, якими ці контакти об’єднані на схемі.
Розв¢язок: для даної контактної схеми маємо таку булеву функцію:
y = (x1 Ú x2) 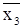 Ú
Ú  x3 Ú (
x3 Ú ( x3 Ú x2
x3 Ú x2 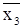 )x4.
)x4.
õ Завдання
1. Позначте вершини й ребра графа (рис. 3.) буквами або цифрами і виконайте наступні умови:

Рис. 3. Розділений граф
а) запишіть усі ребра як невпорядковані пари вершин та відмітьте кратні ребра й петлі;
б) визначте степені всіх вершин, а також суми степенів усіх вершин та всіх непарних вершин графа (що можна сказати про ці суми?);
в) чи є граф однорідним? Якщо ні, то додаванням ребер перетворіть його в однорідний;
г) до якого типу належить граф (простий, мультиграф, псевдограф)?
д) запишіть матрицю суміжності графа.
2. Побудуйте графи, що відповідають наступним матрицям суміжностей. Охарактеризуйте одержані графи:
а)
| e1 | e2 | e3 | e4 | e5 | e6 | |
| v1 | ||||||
| v2 | ||||||
| v3 | ||||||
| v4 | ||||||
| v5 | ||||||
| v6 |
б)
| e1 | e2 | e3 | e4 | e5 | |
| v1 | |||||
| v2 | |||||
| v3 | |||||
| v4 | |||||
| v5 |






