Міністерство освіти і науки України
Полтавський національний технічний університет
Імені Юрія Кондратюка
Кафедра економічної кібернетики
Лабораторний практикум
із дисципліни ¢¢Економічна кібернетика¢¢
для студентів спеціальності 6.050.100 ¢¢Економічна кібернетика¢¢
(II частина)
Полтава 2008
Лабораторний практикум із дисципліни ¢¢Економічна кібернетика¢¢ для студентів спеціальності 6.050.100 ¢¢Економічна кібернетика¢¢ (II частина). — Полтава: ПолтНТУ, 2008. — 39 с.
Укладачі: І. І. Скрильник, ст. викладач
Відповідальний за випуск: Р. Г. Савенко, зав. кафедри економічної кібернетики, доктор техн. наук, професор
Рецензенти: Р. Г. Савенко, д. т. н., професор, М. В. Лисенко, к. мат. н., доцент
Затверджено радою університету
Протокол № 2 від 17.10.2008 р.
Коректор Є. В. Найчук
Вступ
Одним із завдань вивчення дисципліни ¢¢Економічна кібернетика¢¢ є ознайомлення з елементами математичного апарату кібернетики: теорією множин, алгебраїчними системами, теорією графів, основами математичної логіки, елементами числення висловлювань та логіки предикатів, задачами оптимального керування. Математичні методи оброблення, аналізу й перетворення дискретної інформації необхідні в усіх галузях наукової, господарської діяльності та в соціальній сфері. З цією метою для самостійної роботи студентів запропоновано значну кількість вправ і задач. Вивчення курсу базується на знаннях, отриманих під час вивчення шкільної математики й курсу лекцій в університеті. Студенти повинні навчитися застосовувати на практиці одержані знання, користуватися розглянутим математичним апаратом та теоретичними положеннями у своїй професійній діяльності.
Лабораторна робота № 1
Елементи теорії множин
Теорія множин є основою для всіх розділів дискретної математики та комп’ютерних наук у цілому. Глибокі дослідження в самій теорії множин пов’язані з основами математики. Дана теорія має безліч корисних застосувань у програмуванні. Вона використовується для побудови систем управління базами даних, під час побудови й організації роботи комп’ютерних мереж, зокрема мережі Інтернет.
õ Приклади задач
1. Побудуйте 2А для множини А, якщо A = {a, b, c}.
Розв¢язок
Множину всіх підмножин множини X називають множиною-степенем, або булеаном множини X, і позначають 2X. Задана множина A = {a, b, c}, система всіх її підмножин є
2А = {Æ, {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c} },
так що 2А містить 8 елементів.
Порожня множина має тільки одну підмножину — саму порожню множину, тому 2Æ = {Æ}. Для довільної множини X із n елементів кількість усіх її підмножин (тобто |2X|) дорівнює 2n : |2X| = 2|X| = 2n.
2. Нехай дані множини A = {a, b, m}; B = {m, c, p}. Записати A È B, A Ç B, A\B. Операції зобразити, використовуючи діаграми Венна.
Розв’язок
A È B = {a, b, c, m, p}. A Ç B = {m}. A\B = {a, b}.
Різницю множин можна виразити через операції заперечення та перетину таким чином: A\B = A Ç 
.
Otilde; Завдання
1. Які з наведених нижче співвідношень неправильні й чому:
а) xÎ{2, a, x};
б) 3Î{1,{2, 3}, 4};
в) xÎ{1, sinx};
г) {x,y}Î{a, {x, y}, b}?
2. Чи рівні між собою множини A та B (якщо ні, то чому):
а) A={2, 5, 4}, B={5, 4, 2};
б) A={1, 2, 4, 2}, B={1, 2, 4};
в) A={2, 4, 5}, B={2, 4, 3};
г) A={1, {2, 5}, 6}, B={1, {5, 2}, 6};
д) A={1, {2, 5}, 6}, B={1, 2, 5, 6}?
3. Чи пов¢язані множини A й B відношенням уключення (якщо так, то вказати, яка з них є підмножиною іншої):
а) A={a, b, d}, B={a, b, c, d};
б) A={a, c, d, e}, B={a, e, c};
в) A={c, d, e}, B={c, a}?
4. У яких відношеннях знаходяться між собою наступні три множини:
A={1, 3}, B — множина непарних додатних чисел, C — множина рішень рівняння x2 - 4x + 3 = 0?
5. До яких видів належать наступні множини:
а) A — множина конденсаторів у радіоприймачі (множина радіодеталей);
б) В — множина квадратів цілих чисел (множина додатних чисел);
в) С — множина розв’язків рівняння 2x –3 = 0;
г) D — множина дерев на Місяці?
6. Прийнявши множину перших 20-ти натуральних чисел у якості універсума, запишіть наступні його підмножини:
а) A — множина парних чисел;
б) В — множина непарних чисел;
в) С — множина квадратів чисел;
г) D — множина простих чисел.
7. Використовуючи попередню задачу, запишіть множину, одержану в результаті наступних операцій над множинами:
1) A È B;
2) A Ç B;
3) A Ç C;
4) A Ç D;
5) C \ A;
6) C \ B;
7) C +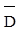 
.
8. У хімічному продукті можуть бути домішки чотирьох видів, позначені через a, b, c, d. Прийнявши A={a, b, c, d}, утворіть множину всіх її підмножин R(А).
9. Покажіть, що з відношення A Ç B = С випливає, що С Ì А і С Ì В.
10. Чи є сукупність співвідношень P Ì M1 , M1 Ç M2 Ì P, M2 Ç P = Æ несуперечною? Чи можна її спростити? Викладіть спочатку логічні міркування, а потім скористайтеся кругами Ейлера.
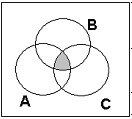
11. Що можна сказати про відношення між множинами A, B, C, представленими кругами Ейлера? Запишіть за допомогою операцій над множинами вирази для множин відповідних заштрихованих областей:
a) б) с)
12. За допомогою кругів Ейлера покажіть, що:
а) Æ Ì A Ç B Ì A È B;
б) A + A = Æ;
в) якщо A Ç B = С, то C Ì A і C Ì B;
г) (M\N) Ç(N\M) = Æ.
13. За допомогою кругів Ейлера покажіть, що:
а) (A È B) Í (A È B È C);
б) (A Ç B Ç C) Í (A Ç B).
14. Виходячи з відношення належності, доведіть справедливість наступних виразів:
а) A È (B\A) = A È B;
б) A Ç (B\A) = Æ.
15. Задайте у вигляді X = {x | P(x)} такі множини:
а) множину натуральних чисел, більших за 100;
б) множину парних додатних чисел;
в) множину натуральних чисел, кратних 10.
16. Запишіть елементи множин:
а) {x | x Î N, 3 £ x £ 12};
б) {x | x — десяткова цифра}.
õ Завдання для самостійної роботи
1. Скільки елементів містять такі множини:
а) {x};
б) {{x}};
в) {x, {x}};
г) {{x}, x, {{x, {x}}}?
2. Які з наведених тверджень правильні? Доведіть.
а) якщо A Ì B і B Ì C, то A Ì C;
б) якщо A Í B і B Í A, то A = B;
в) якщо A Í B і B Í C, то A Í C.
3. Дана множина D = {7, 13, 25, 34, 101, 112}. Які з наведених множин є підмножинами множини D:
а) {1, 7, 13};
б) {0, 1, 12};
в) {25, 112, 34};
г) {a, b, c, n};
д) {7, 13, 25, 34, 101, 112};
е) Æ?
4. Визначте, які з наведених множин дорівнюють одна одній:
а) A = {x | існує y такий, що x = 2y, y Î N};
б) C = {1, 2, 3};
в) D = {0, 2, -2, 3, -3, 4, -4, …};
г) E = {2x | x Î Z}.
5. Побудуйте 2А для множини А, якщо:
а) A = {{Æ}};
б) A = {1, 2, 3, 4};
в) A = {¢¢день¢¢, ¢¢ніч¢¢};
г) A = {1, {2, 3}, 4}.
6. Скільки підмножин містить:
а) множина днів тижня;
б) множина місяців року?
7. Утворіть множину святкових днів року. Чи перетинається ця множина із множиною вихідних днів цього ж року?
8. Зобразіть такі множини у вигляді кругів Ейлера:
а) A = {0, 1, 2}, B = {1, 2, 3, 4, 5};
б) A = {a, b, c, d, e}, B = {d, a, e};
в) N — натуральні числа, Z — цілі числа, R — дійсні числа;
г) X — множина птахів, Y — множина звірів, Z — множина ссавців, F — множина кроликів, G — множина живих організмів, які живуть у морях і океанах.
9. Для множин A= {1, 2, 3, 4, 5}, B= {0, 3, 6} знайдіть:
а) A È B;
б) A Ç B;
в) A\B;
г) B\A.
10. За допомогою діаграм Венна доведіть, що 
A\B = A Ç 
.
11. Знайдіть множини A і B, якщо A\B = {1, 5, 7, 8}, B\A = {2, 10},
B Ç A = {3, 6, 9}.
12. Які висновки можна зробити про множини A і B, якщо правильна одна з таких рівностей:
а) A È B = A;
б) A Ç B = A;
в) A\B = B\A;
г) A\B = A?
Лабораторна робота № 2
Алгебра множин
Множина 2U усіх підмножин універсальної множини U із заданими на ній чотирма операціями складає алгебру множин та позначається cr. Клас множин cr називається алгеброю множин, якщо:
1. U Î cr.
2. З A, B Î cr виходить A È B Î cr.
3. З A, B Î cr виходить A\B Î cr.
Алгебра множин cr широко застосовується у програмуванні, зокрема під час роботи з різноманітними базами даних, і становить основу для побудови багатьох математичних структур. За допомогою операцій над множинами створюються складні алгебраїчні вирази. Відносно одна одної операції мають такий пріоритет:
1. 
; 3. A È B;
2. A Ç B; 4. A\B.
В алгебрі множин cr автоматично виконують такі тотожності, які дозволяють віднести cr до класу так званих булевих алгебр.
1. Комутативний закон для об’єднання й перетину множин.
А È В = В È А; А Ç В = В Ç А.
2. Асоціативний закон для об¢єднання й перетину множин
А È (В ÈС) = (А È В) ÈС; А Ç (В ÇС) = (А Ç В) ÇС.
3. Дистрибутивний закон для об¢єднання та перетину множин
А È (В ÇС) = (А È В) Ç(А È С); А Ç (В ÈС) = (А Ç В)È(А Ç С).
4. Властивості пустої множини й універсума відносно об’єднання
А È Æ = А; А È U = U;
А È 
= U; 
= U.
5. Властивості пустої множини й універсума відносно перетину
А Ç U = A; А Ç Æ = Æ;
А Ç = Æ; 
=Æ.
6. Закон ідемпотентності для об’єднання та перетину множин
А È А = А; А Ç А = А.
7. Закон поглинання
А È(АÇ В) = А; А Ç(А È В) = А.
8. Закони де Моргана
; 
.
Наступні властивості:
1. Якщо А È В = U і А Ç В =Æ, то В=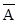 
.
2. 
=U \ А.
3. 
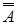=А.
4. А \ В = А Ç В.
5. А+В = (А Ç 
)È( Ç В).
6. А+В = В+А.
7. А+В+С = А +(В+С).
8. А+Æ = Æ+А = А.
9. А Ì В, тоді і тільки тоді, якщо А Ç В = А або А È В = В, або А Ç = Æ.
10. А = В, тоді і тільки тоді, якщо (А Ç )È( Ç В) = Æ.
õ Приклади задач
1. Довести, що А È А = А.
Розв’язок
А È А =(А È А) Ç U = (А È А) Ç (А È ) = А È(А Ç ) = А ÈÆ = А.
2. Довести, що А È (В ÇС) = (А È В) Ç(А È С).
Розв’язок
Припустимо, що xÎА È (В ÇС),тоді xÎА або xÎ(В ÇС).Якщо xÎА, то x належить до об¢єднання Аз будь-якою множиною, тобто xÎА È Ві xÎА È С, з цього випливає, що xє елементом перетину множин А È ВіА È С, тобто xÎ(А È В) Ç(А È С).
Якщо xÎВ ÇС, то xÎВ і xÎС, а значить xÎА È Ві xÎА È С, тобто x є елементом перетину тих же множин. Таким чином, доведено, що
А È (В ÇС)Ì(А È В) Ç(А È С). Аналогічно доводимо й відношення
А È (В ÇС)É(А È В) Ç(А È С). Згідно з визначенням рівності множин маємо потрібну тотожність А È (В ÇС) = (А È В) Ç(А È С).
4. Спростити вираз 
.
Розв’язок
5. Спростити вираз 
Розв’язок
.
õ Завдання
1. Доведіть за допомогою тотожних перетворень співвідношення:
а) A\(A\B) = B\(B\A);
б) (A Ç B Ç C) È (
Ç B Ç C) = B Ç C;
в) (A Ç B Ç C 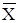Ç 
) È ( Ç C) È (
Ç C) È (C Ç X) = C.
2. Виходячи зі співвідношення належності, доведіть справедливість наступних елементів:
а) A È (B\A) = A È B;
б) A Ç (B\A) = Æ;
в) A È B = B È A;
г) A Ç B = B Ç A;
д) A È (B È C) = (A È B) È C;
е) A È (B Ç C) = (A È B) Ç (A È C);
є) A Ç (B È C) = (A Ç B) È (A Ç C).
3. Доведіть тотожність:
а) 
б) A È Æ = A.
4. Спростіть вираз:
а) (M\N) Ç (N\M);
б) 
;
в) 
г) 
д) 
;
е) 
.
õ Завдання для самостійної роботи
1. Доведіть справедливість тотожності:
.
2. Виходячи, що A + B = (A\B) È (B\A), доведіть:
а) A + B = B + A;
б) A + (B + C) = (A + B) + C;
в) A Ç (B + C) = (A Ç B) + (A Ç C);
г) A + Æ =A.
3. У якому відношенні знаходяться множини A і B, якщо A\B = B\A = Æ?
4. Доведіть за допомогою тотожних перетворень співвідношення. Результат перевірте за допомогою кругів Ейлера:
а) (A\B)\С = (A\C)\(B\C);
б) A Ç 
.
4. Показати справедливість тотожності 
.
Лабораторна робота № 3
Нечіткі множини
Основи нечіткої логіки були закладені у кінці 60-х років у роботах відомого американського математика Лафти Заде. Строге визначення поняття нечіткої множини, введене Заде, має наступне формулювання:
нехай Е — є множина, скінчена або ні, і x — елемент Е. Тоді нечіткою підмножиною А множини Е називається множина впорядкованих пар 
, де 
— ступінь належності x в А.
Таким чином, якщо приймає свої значення у множині М значень функції належності або у множині належності, то можна сказати, що x приймає значення в М за допомогою функції . Ця функція називається функцією належності.
Операції над нечіткими множинами
Нехай А і В — нечіткі множини на універсальній множині Е. Говорять, що А міститься в В, якщо 
.
Позначення: 
.
Іноді використовують термін ¢¢домінування¢¢, тобто у випадку якщо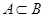 
, говорять, що В домінує А.
Рівність
А і В рівні, тобто 
.
Позначення: 
.
Доповнення
Нехай 
, А і В — нечіткі множини, задані на Е. А і В доповнюють один одного, якщо 
.
Позначення: 
або 
.
Очевидно, що 
(доповнення визначене для 
), але очевидно, що його можна визначити для будь-якого впорядкованого М).
Перетин
— найбільш нечітка підмножина, яка міститься одночасно в А і В.
.
Об’єднання
— найменша нечітка підмножина, яка включає як А, так і В, з функцією належності:
.
Різниця
з функцією належності
.
Диз’юнктивна сума
з функцією належності
.
Властивості операцій
Комутативний закон для об’єднання і перетину множин
А È В= В È А;
А Ç В= В Ç А.
Асоціативний закон для об’єднання і перетину множин
А È (В È С)=(А È В) È С;
А Ç (В Ç С)=(А Ç В) Ç С.
Дистрибутивний закон для об’єднання і перетину множин
А È (В Ç С)=(А È В) Ç(А È С);
А Ç (В È С)=(А Ç В) È(А Ç С).
Властивості пустої множини й універсума відносно об’єднання
А ÈÆ = А;
А ÇÆ = Æ;
А È Е = Е;
А Ç Е = А.
Закон ідемпотентності для об’єднання і перетину множин
А È А = А;
А Ç А = А.
Закон інволюції
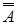=А.
Теорема де Моргана
;
.
õ Приклади задач
Нехай
A = 0,4/ x1 + 0,2/ x2+0/ x3+1/ x4;
B = 0,7/ x1+0,9/ x2+0,1/ x3+1/ x4;
C = 0,1/ x1+1/ x2+0,2/ x3+0,9/ x4.
Визначити , , 
, 
, 
, 
, 
, 
.
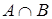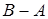Розв’язок
1. , тобто А міститься в В або В домінує А, С незрівняна ні з А, ні з В, тобто пари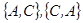 
— пари недомінуючих множин.
2. 
0,6/ x1 + 0,8/x2 + 1/x3 + 0/x4;
0,3/x1 + 0,1/x2 + 0,9/x3 + 0/x4.
3. 
0,4/x1 + 0,2/x2 + 0/x3 + 1/x4.
4. 
0,7/x1 + 0,9/x2 + 0,1/x3 + 1/x4.
5. 
0,3/x1 + 0,1/x2 + 0/x3 + 0/x4;
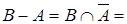0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4.
6. 
0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4.
õ Завдання для самостійної роботи
1. Для універсальної множини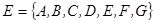 
та нечітких підмножин
знайти
а) 
;
б) 
;
в) 
;
г) 
;
д) 
;
е) 
;
є) 
;
ж) 
.
2. Довести властивість
а) 
;
б) 
;
в) 
.
3. Для трьох нечітких підмножин із вправи 1 обчисліть
а) 
;
б) 
.
4. Спростіть вираз
.
5. Довести
а)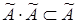 
;
б) 
;
в) 
.
6. Виходячи, що A + B = (A\B) È (B\A), доведіть
а) A + B = B + A;
б) A Ç (B + C) = (A Ç B) + (A Ç C);
в) A + Æ =A.
Лабораторна робота № 4
Булева алгебра. Закони булевої алгебри. Складання таблиці істинності функції
Для зображення інформації в комп’ютерах використовується двійкова система числення. Таким чином, усі операції, які виконує комп’ютер, проводяться на множині {0, 1}. Ці перетворення зручно формально зображати за допомогою апарату двійкової логіки, який був розроблений Д. Булем у середині XIX ст. Ця алгебраїчна структура називається булевою алгеброю і використовується під час розв’язання різних задач обробки інформації, під час роботи з базами даних, у логічному програмуванні, при проектуванні інтелектуальних систем, для конструювання й аналізу роботи комп’ютерів та інших електронних пристроїв. У булевій алгебрі використовують такі закони:
1. Комутативність кон’юнкції й диз’юнкції
x Ú y = y Ú x; x Ù y = y Ù x.
2. Асоціативність кон’юнкції та диз’юнкції
x Ú (yÚ z) = (x Ú y)Ú z; x Ù(yÙ z) = (x Ù y)Ù z.
3. Дистрибутивність кон’юнкції й диз’юнкції відносно одна одної
x Ù(yÚ z) = (x Ù y)Ú (x Ù z); x Ú(yÙ z)=(x Ú y)Ù (x Ú z).
4. Ідемпотентність кон¢юнкції й диз’юнкції
x Ú x = x; x Ù x = x.
5. Закон виключення третього
xÚ 
= 1.
6. Закон протиріччя
x Ù = 0.
7. Тотожності з константами
x Ú 0 = x; x Ù 1= x; x Ù 0= 0; x Ú 1= 1.
8. Закони елімінації (поглинання)
x Ú (x Ù y) = x; x Ù (x Ú y) = x.
9. Закон подвійного заперечення
.
10. Закони де Моргана
; 
.
11. Тотожності
x Ú ( Ù y) = x Ú y;
(x Ù y)Ú (x Ù z)Ú (yÙ 
)=(x Ù z)Ú (yÙ );
; 
; x Ú 1= 1; x Ù 0= 0 і т.д.
Тотожності можна доводити за допомогою перетворень виразів і складання таблиць істинності.
õ Приклади задач
1. Доведіть закон ідемпотентності x Ú x = x Ù x = x.
Розв’язок
x Ú x = x Ú x Ù 1= (x Ú x) Ù 1= (x Ú x) Ù (xÚ ) = x Ù (xÚ ) = x Ù 0 = x;
x Ù x = x Ù x Ú 0 = (x Ù x) Ú 0 = (x Ù x) Ú (xÙ ) = xÚ (xÙ ) =
xÙ(xÚ ) = x Ù 1= x.
2. Доведіть, що x Ú 1= 1.
Розв’язок
x Ú 1= x Ú (x Ú ) = (x Ú x) Ú = x Ú = 1.
3. Доведіть, що x Ù 0 =0.
Розв’язок
x Ù 0 = x Ù (x Ú ) = (x Ù x) Ú = x Ú = 0.
4. Довести закон поглинання x Ú (x Ù y) = x Ù (x Ú y)= x.
Розв¢язок
x Ú (x Ù y) = (x Ù 1) Ú (x Ù y) = x Ù (1 Ú y) = x Ù 1= x;
x Ù (x Ú y) = (x Ú 0) Ù (x Ú y) = x Ú (0Ù y) = x Ú (y Ù 0) = x Ú 0 = x.
5. Довести, що 
.
Розв’язок
Це співвідношення доводимо таким чином:
xÚ =1, із закону комутативності випливає, що Ú x=1, порівнюючи Ú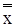 
=1, маємо x = .
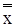6. Довести закони де Моргана 
.
Розв¢язок
На основі властивостей заперечення рівності функцій 
та 
повинно означати, що
(x Ú y)Ú() = 1 та (x Ú y)Ù() = 0. Дійсно,
(x Ú y)Ú() = ((x Ú y)Ú )Ù((x Ú y)Ú 
) = ((x Ú )Ú y)Ù(xÚ(yÚ )) =
(1Ú y)Ù(xÚ1) = 1Ù1=1;
(xÚy)Ù() = (x Ù())Ú(yÙ(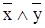
)) = ((xÙ )Ù )Ú ((yÙ )Ù ) =
(0Ú )Ú (0Ù ) = ( Ù0)Ú( Ù0) = 0 Ú 0 = 0.
Отже, співвідношення доведено. Аналогічно доводиться другий закон.
7. Довести за допомогою таблиці істинності закон де Моргана .
| x | y |
|
|
| x Ú y |
|
Побудована таблиця істинності доводить справедливість тотожності.
Операцію кон’юнкції часто називають логічним множенням, а операцію диз’юнкції — логічним додаванням. Ще одне спрощення допускається: знак кон’юнкції у формулах можна опустити й замість x Ù yписати xy. Операції виконуються у такій послідовності: заперечення, кон’юнкція, диз’юнкція, імплікація й еквівалентність.
õ Завдання
1. Підстановкою у формулу 
змінних запишіть нові формули, спростіть їх, якщо це можливо:
а) 
, b = z;
б) 
; 
;
в) a = x, 
.
2. Запишіть таблиці істинності для наступних формул:
а) 
;
б) 
;
в) 
.
3. Перевірити за допомогою таблиць істинності наступні тотожності:
а) 
;
б) 
;
в) x Ú (y ~ z) = (x Ú y) ~ (x Ú z);
г) x ® (y ~ z) = (x ® y) ~ (x ® z);
д)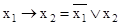 
;
е) x1 ~ x2 = 
.
4. Спростити формули:
а) 
;
б) 
;
в)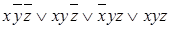 
;
г) 
.
5. Перетворіть формули так, щоб операція заперечення застосовувалася лише до логічних змінних:
а) 
;
б)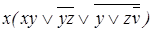 
.
6. З простих виразів x1=¢¢випробування проведені¢¢ та x2=¢¢програма виконана¢¢ створіть складні вирази за такими формулами:
а)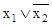 
;
б) 
;
в) x1 ® x2;
г) x1 ~ x2.
7. Запишіть формулу, що відповідає висловлюванню: ¢¢Програма буде виконана тоді і тільки тоді, коли скінчаться іспити й показники будуть задовільні; якщо програма не буде виконана, співробітники не одержать премію або будуть переглянуті технічні умови¢¢.
õ Завдання для самостійної роботи
1. Перевірте за допомогою таблиць істинності, чи справедливі такі співвідношення:
а) x Ù (y ~ z) = (x Ù y) ~ (x Ù z);
б) x ® (y Ú z) = (x ® y) Ú (x ® z);
в) x ® (y Ù z) = (x ® y) Ù (x ® z);
г) x Å (y Ù z) = (x Ä y) Ù (x Ä z);
д) x ® (y ® z) = (x ® y) ® (x ® z).
2. Побудуйте таблиці істинності для формул:
а) 
;
б) 
;
в) 
.
3. При x1 = 1, x2 = 0, x3 = 0, x4 = 1 знайдіть значення кожної з наступних формул:
а) 
;
б)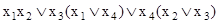 
;
в) 
;
г) 
~ 
;
д) 
(x2 ~ x3);
е)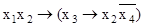 
.
4. Спростіть за допомогою законів логіки Буля наведені нижче вирази. Потім за допомогою таблиць істинності порівняйте одержані вирази з вихідними:
а) 
;
б) 
;
в) 
;
г) 
;
д) 
;
е) 
;
є) 
;
ж) 
.
Лабораторна робота № 5
