Свойства электромагнитных волн.

Материальные уравнения.

Уравнения М-ла указывают на существование единого ЭМП. В материальных ур-ниях учитывают тот факт,

что явления, означающие взаимосвязь полей, всегда развертываются в некоторой среде. Поэтому в систему УМ включают соотношения между силовыми характеристиками полей – абсолютными и «привязанными» к среде К этому же относят и дифференциальную запись закона Ома для цепи, содержащей источник ЭДС (источник сторонних сил, характеризуемых напряжённостью поля здесь проводимость (характеристика проводящего свойства среды), Cвязь смещения и напряжённости ЭП м-т формулироваться таким ур-нием:

Система уравнений Максвелла.

Итак, в полной (для нашего курса) формулировке основные уравнения электродинамики запишутся так (включено также полученное в электростатике соотношение для связи скалярного потенциала j с напряжённостью поля ):

Здесь представлена интегральная запись основных уравнений, используемая обычно для обсуждения принципиальных проблем взаимосвязи электрич. и магнитного полей в системе единого ЭМП и – довольно редко – для конкретных расчетов входящих в неё величин. Смысл любых уравнений в том, чтобы определить неизвестные величины, по нек-рым параметрам и условиям, к-рые представляют физич. ситуацию. Задача поиска обычно ставится так – заданы параметры среды 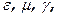распределение зарядов r и токов а также граничные условия для связи значений переменных на поверхностях раздела сред с разными параметрами, и требуется определить зависимости и (или) Для подобных расчетов используют систему УМ в дифференциальной форме, записанную Г.Герцем.

Итак, уравнениями Максвелла, основанными на ряде фундаментальных эффектов электромагнетизма, устанавливается единство электромагнитного поля. Разделение ЭМП на составляющие поля – относительно, считается обоснованным при теоретич. рассмотрении нек-рых эффектов.

Перенос энергии ЭМП. Физическая суть системы УМ еще и в том, что ими выражен закон сохранения энергии ЭМП. На их основе доказывается следующее соотношение: В его левой части стоит величина мощности источника ЭДС, к-рая д-на расходоваться на выделение тепловой мощности («джоулевой» теплоты) Р = (справа), на увеличение энергии ЭМП в цепи (с плотностью и, наконец, на излучение энергии ЭМП (3-е слагаемое). Величина мощности излучаемого поля устанавливается теоремой Умова-Пойнтинга Здесь Физич. смысл вектора с размерностью [ Вт/м² ] в том, что это ¾ поток мощности ЭМ поля ч/з единичную площадку, нормаль к к-рой параллельна потоку. Эту величину называют вектором Пойнтинга, излучаемую мощность ЭМ поля S ¾ потоком вектора Пойнтинга. Этот поток в теореме определяется сквозь замкнутую поверхность s, окружающую (как правило, это ¾ сфера) электрич. цепь с источником ЭДС.

Ø Соотношение (5) читается т. о .: в ед-це объёма за ед-цу времени работа сторонних сил в источнике ЭДС идет на покрытие джоулевых потерь в цепи, на увеличение ЭМ энергии и на покрытие убыли энергии, вытекающей наружу. В этом ¾ выражение закона сохранения энергии ЭМ поля. Структура соотношения (5) указывает, что в электрич. цепи обязат-но д-но происходить испускание энергии ЭМ поля. Этот процесс характеризуется особой величиной - вектором Пойнтинга. В ЭМ поле, т.о., возможен перенос энергии.

Ø Когда по проводнику идет ток, в каждом участке проводника выделяется тепло. Оч-но, выделяющаяся энергия д-на кaк-то транспортироваться от источника к данному участку. Оказывается, существует стационарный поток ЭМ поля в простр-ве вокруг проводника, описываемый вектором Пойнтинга. Электрич. поле вдоль проводника имеет тангенциальную (вдоль проводника) и нормальную (перпендикулярно к его поверхности) составляющие ( одной обусловлено течение тока вдоль пр-ка, другая зависит от поверхностных ЭЗ ). Магнитное поле направлено по касательной к силовым линиям, замыкающимся вокруг электрич. тока. Получается, что существуют две составляющие потока ЭМ энергии - внутрь проводника из диэлектрика (или вакуума) его окружающего и вдоль проводника. Втекающая в проводник энергия превращается в нем в тепло ¾ чем меньше сопротивление, тем меньше этот поток. На участке со сторонними силами этот поток направлен из материала источника наружу. T.o., соединительные проводники в электрич. цепях, напр-р, провода в технич. электрич. сетях, являются лишь направляющими элементами («ведущими» ЭМ поле) цепи, вдоль к-рых от источника передаётся энергия ЭМ поля.
Волновое уравнение для электромагнитных волн.

Формулировка основных ур-ний электромагнетизма дала возможность предсказать существование ЭМ волн. Из УМ следуют такие ур-ния для силовых векторов: 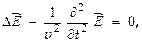а также 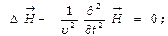известно, что в механике дифференциальные ур-ния такого типа называют волновыми. Действит-но, ими описывается распространение в пространстве переменных – силовых векторов ЭМП как волновой процесс. Здесь оператор (в декартовой сиcтеме координат), скорость движения волны, обычно выделяются величина скорость ЭМ волны в вакууме, а также 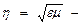показатель преломления; так что Решение ур-ний для силовых векторов в общем виде представляется функциями, именуемыми волновыми (ВФ) и радиус-вектор, волновое число ( или модуль волнового вектора направление к-рого совпадает с единич. вектором направления ЭМ волны Частота w колебаний в ЭМ волне выступает свободным параметром (константа интегрирования), т.е. ВФ удолетворяет волновому ур-нию при любых значениях w. B одномерном представлении (когда направление движения волны совпадает с осью Ох) волновое ур-ние запишется так его решение (ВФ) представляется гармонической бегущей волной: Для напряжённости МП аналогично: Здесь определяется как проекция волнового вектора на ось Ох.

Свойства электромагнитных волн.

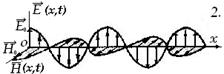
Используя уравнения системы Максвелла и выражение ВФ в общем виде, м-но показать, что ЭМ волна поперечна, т.е. колебания векторы ЭП и МП в волне перпендикулярны по отношению к волновому вектору. Cиловые векторы, перемещающиеся с волной, также взаимно перпендикулярны ( рис .2). ВФ, в том виде, как она записана (6), обычно называют плоской; компонентой в фазе – - определяется т.н. волновой фронт (поверхность равной фазы), а ур-нием в декартовой системе координат описывается плоскость. Более реальными считаются ЭМ волны в виде волн, где волновой фронт представляет собой сферу (так наз. сферические ЭМ волны).

Ø Для плоских ЭМ волн доказывают, что поэтому плотность энергии в ЭМ волне- , а в-р Пойнтинга (на рис. 2 направление совпадает с осью Ох). При нормальном падении потока ЭМП на поглощающую поверхность телу передается импульс (количество движения) 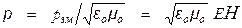= v ¾ т.е. величина импульса равна плотности энергии поля в ЭМ волне, при отражении ЭМ поля от поверхности импульс вдвое больше (p = 2× v).

Ø Ур-ния для векторов напряженности ЭП и индукции МП – волновые, т.е. ЭМ поле, к-рое характеризуется этими векторами, может распространяться в виде волны, и скорость распространения этих векторных величин определяется исключительно свойствами среды.

Ø Волны возникают лишь тогда, когда их возбуждают, и из того, что они удовлетворяют волновому ур-нию не вытекает к.-л. практич. способ возбуждения ЭМВ. ЭМ волнавозбуждается зарядами и токами, но после ее образования ЭМ волна существует и тогда, когда породивших её источников уже нет.

Ø Излучение ЭМ волн реализуется в особых устройствах. Исторически первое из них получило название осциллятора (или диполя) Герца (схема на рис.3 представляет так наз. открытый колебательный контур, устроенный по принципу Герца ¾ заряд на шарах гармонически колеблется во времени, излучение происходит при электрическом разряде между шарами). Эти устройства представляют собой электрические системы, в к-рых заряды могут двигаться ускоренно. Именно ускоренно движущиеся заряды излучают ЭМП. Теоретическим признаком того, что система является источником излучаемого ЭМП, т.е., излучателем ЭМ волн, есть независимость потока мощности S излучаемого ЭМП (в теореме Умова-Пойнтинга) от размера поверхности s, по к-рой этот поток определяется. Обычно эту поверхность выбирают как сферу. Т.е., признаком излучающей системы является независимость потока вектора Пойнтинга S от радиуса сферы, сквозь поверхность к-рой определяется поток. Энергия ЭМП тогда «уходит» из системы, т.е. излучается в пространство.