Проводники в электростатическом поле.

Свойства заряда.

1. ЭЗ может быть положительным или отрицательным (электральность определяется 2 противоположными ЭЗ),

2. Величина ЭЗ дискретна (кратна ЭЗ электрона е = 1.6×10 ^-19 Кл).

3. Закон сохранения ЭЗ является в физике фундаментальным - в изолированной системе алгебраическая сумма ЭЗ постоянна (в частной формулировке: скорость увеличения или убыли ЭЗ из нек-рого объема характеризует величину электрич. тока).

Все вещества построены из электрически заряженных частиц, важнейшими из которых являются отрицательно заряженные электроны и положительно заряженные протоны. Заряды электрона и протона по модулю равны. Объяснения тому, что нек-рые элементарные частицы обладают ЭЗ, а другие нет, пока не существует. В незаряженном состоянии, суммарный заряд протонов полностью компенсируется зарядом электронов, или число электронов равно числу протонов. ЭЗ образуется избытком или недостатком электронов во внутренней структуре тела. Заряд Q, регистрируемый у нек-рого тела, представим поэтому как Q = N e, где N – число избыточных или недостающих электронов. Вводится характеристика плотности заряда r = n×e [ Кл /м³], где n [м^-3] – число электронов (избыточных или недостающих) в ед-це объёма.

Свойство сохранения ЭЗ объясняется в рамках современных представлений о строении вещества. В изолированной системе тел суммарный ЭЗ протонов полностью компенсирован ЭЗ электронов, или число электронов равно числу протонов. Но на телах системы ЭЗ м-т быть перераспределены так, что ряд тел характеризуется наличием заряда. Поэтому для таких систем закон сохранения ЭЗ есть закон сохранения электрически заряженных частиц на всех её элементах. Более подвижными частицами являются электроны, поэтому в большинстве случаев при электризации происходит переход части электронов с одного тела на другое. Тело, имеющее избыток электронов, заряжено отрицательно, тело с недостатком электронов – положительно.

Однако закон сохранения ЭЗ имеет и более фундаментальный смысл. Элементарные частицы при взаимодействиях могут «превращаться» друг в друга – происходит рождение одних частиц и исчезновениe других. Во всех этих превращениях суммарный ЭЗ сохраняется – если появляется положительно заряженная частица, то обязательно появляется отрицательно заряженная частица. Причина такого поведения частиц пока неизвестна.

4. Инвариантность электрического заряда. Экспериментальныe данные свидетельствуют, что ЭЗ обладает инвариантностью, т.е., его величина не зависит от выбора СО, не зависит от скорости движения частиц.

Одним из основных принципов всей физики является принцип относительности – во всех инерциальных системах отсчета (СО) все физические явления протекают одинаково. Или, что равносильно, равномерное движение не влияет на протекание физических процессов. Поэтому, при введении любой физической величины важным является вопрос о зависимости этой величины от скорости движения тела, или от выбора системы отсчета.

Не случайно ниже в формулировке закона Кулона указывается на неподвижность заряженных тел. При движении зарядов между ними действуют также и магнитные силы.

5. Основное свойство ЭЗ - создание в окружающем пространстве электрического поля (ЭП). Понятие поля как материального (физического) образования, проявляющего себя по силовому воздействию на определенные объекты и, в принципе, бесконечного в пространстве, опирается на понятие силы – меры воздействия или взаимодействия тел. Физическое поле в таком понимании – прежде всего силовое.

В общем случае рассматривают электромагнитное поле (ЭМП), Его разделение на электрич. и магнитное, речь о к-рых будет идти далее, условно. Говорят, что электростатич. поле (ЭСП) проявляет себя в случае, если ЭЗ покоятся, магнитное (МП) же - если заряды движутся. Заряды считаются неподвижными благодаря усреднению скоростей зарядов движущихся в среде электронов и ионов в условиях, когда их средняя скорость равна 0. Представление о неподвижных ЭЗ явл-ся, вообще говоря, идеализацией. Поск-ку в абсолютном смысле этого понятия таких ЭЗ не существует, то не существует и ЭСП. Электрич. поле, однако, м-но считать ЭСП, если принять среднюю скорость движения ЭЗ, порождающих поле, равной нулю; и это ЭСП считается приближённой моделью реального поля.

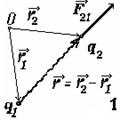
Закон Кулона (ЗК). Сила взаимодействия между 2-мя неподвижными точечными ЭЗ q ₁ и q ₂ в вакууме пропорциональна величинам зарядов и обратно пропорциональна квадрату расстояния 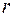между ними ( закон Ш.Кулона, 1785 ): 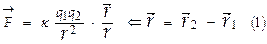(точеч. ЭЗ по геометрич. размерам малы по сравнению с расстоянием ê 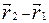÷, k - коэф-нт пропорциональности, зависящий от системы единиц; сила F направлена по прямой между ЭЗ ( рис. 1 - для одинаковых по знаку - отталкивание, для противоположных ЭЗ - притяжение). В СИ - 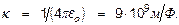Здесь e₀- электрическая постоянная, e₀ = 8.85×10^-12 Ф / м. Закон (1) об электрич. взаимодействиях в электростатике является основным.

напряжённость ЭП. Для постоянного r ( расстояния между нек-рым центральным зарядом Q и пробным произвольным ЭЗ ) оказывается неизменным отношение кулоновской силы F и величины пробного ЭЗ q ₀. Ввиду этого из (1.1) определяется силовая характеристика поля ЭЗ Q - напряжённость Е: 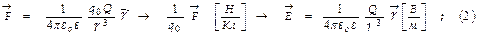очевидно, что

Здесь коэффициент e - относит. диэлектрич. проницаемость (ДП) среды. Формулировка ЗК, т.о., важна для понимания сущности понятия напряжённости ЭП - силовой характеристики, выражающей действие данного поля на единич. заряд в определенной точке пространства в нек-ром веществе. Характеристика в виде (1.3) записана для относит-но неподвижного точечного ЭЗ. Вообще, определение напряженности 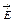как силы, действующей на единичный ЭЗ, верно для любого ЭП, не только ЭСП. Выражение (3) для кулоновской силы, действующей на ЭЗ q в поле заданной напряженности 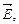называют локальной формулировкой ЗК. Её применяют, напр-р, для расчетов силы Кулона в однородном ЭП, т.е. в поле, напряженность в к-ром не зависит от координат.

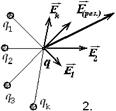
Для расчета поля, создаваемого несколькими точечными зарядами, следует воспользоваться принципом суперпозиции (рис.2): напряженность поля, созданных системой зарядов, равна сумме напряженностей полей, создаваемых каждым зарядом в отдельности:

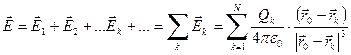. Отметим особенность в графике векторов – вектор напряжённости изображается выходящим от положительных ЭЗ ( направление поля )..

Потенциал ЭП. В механике показано, что любая центральная сила является потенциальной, то есть работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела. Любое электростатическое поле поэтому потенциально.

Выражение для потенциальной энергии электростатич. взаимодействия двух точечных ЭЗ определяют так: . Сила, действующая на заряженное тело с пробным ЭЗ, пропорциональна ЭЗ, следовательно, работа и потенциальная энергия взаимодействия также пропорциональны величине пробного ЭЗ q ₀. Поэтому, если работу по перемещению пробного заряда в поле ЭЗ Q разделить на величину пробного ЭЗ, то получим характеристику поля (не зависящую от ЭЗ q ₀). Аналогично, если разделить потенциальную энергию взаимодействия заряда с полем на величину заряда q ₀, то получим характеристику поля, которая называется потенциалом электрич. поля. Это – скалярная величина, выражаемая отношением потенциальной энергии взаимодействия ЭП 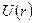и пробного точечного заряда к величине заряда q ₀: Так, очевидно, дляточечного заряда Q потенциал ЭСП, создаваемого Q на расстоянии 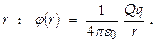Скалярный потенциал ЭП является размерной физич. величиной, по определению размерность потенциала 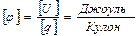= 1 Вольт (СИ). Произведением потенциала поля на величину заряда устанавливается значение потенциальной энергии заряда в данной точке поля, поэтому потенциал – энергетическая характеристика ЭП. Суммарный потенциал системы зарядов находится как алгебраич. сумма составляющих потенциалов.

Связь потенциала с напряжённостью поля выражается как здесь проекция вектора напряжённости на направление r в пространстве, занимаемом полем. В более общем виде для ЭСП записывают выражени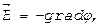е где 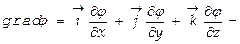вектор, указывающий направление наибольшего возрастания функции. Т.е. градиент потенциала представляет собой вектор, направленный в сторону, обратную наибольшему возрастанию потенциала как функции координат, и численно равен напряженности ЭП.

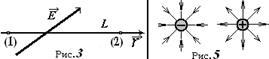
Обратная операция по определению разности потенциалов вдоль траектории L выразится 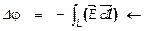циркуляцией вектора Е по контуру траектории L. Циркуляция вектора по контуру используется в качестве интегральной характеристики векторных полей. В случае, если контур траектории – отрезок прямой между точками то разность потенциалов выразится обычным интегралом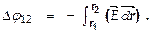

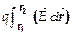
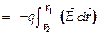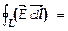
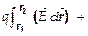
Примечание. Потенциальный характер ЭСП выражается тем, что работа сил ЭСП по перемещению ЭЗq не зависит от формы пути (траектории), а определяется лишь нач. и конеч. точками пути Циркуляция силового вектора по замкнутому контуру выражает работу по перемещению единичного ЭЗ по замкнутой траектории, тогда поск-ку и записывают, что циркуляция вектора напряжённости ЭСПЕ по замкнутому контуру пути L равна нулю: 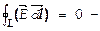это равенство выражает признак потенциальности электростатич. поля, а в общем случае – потенциальности нек-рого физического силового поля.

Теорема Гаусса.

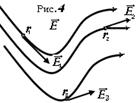
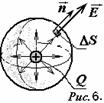
Линии напряжённости ( силовые линии поля ) изображаются так: касательные к ним совпадают с направлением вектора поля ( рис. 4), при этом линии ЭСП начинаются и упираются в ЭЗ ( рис. 5). Силовые линии не пересекаются (в противном случае, в точке пересечения можно построить две касательных, то есть в одной точке, напряженность поля имеет два значения, что абсурдно). Силовые линии не имеют изломов (в точке излома опять-таки можно построить две касательных).

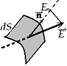
Поток напряжённости ЭП. Ч тобы силовыми линиями м-но было характеризовать не тк направление, но и значение Е, условились проводить их с определённой густотой - сквозь элементар. площадку dS, нормаль n к к-рой образует угол a с вектором , их всего - E × dS cosa = E _n dS. Величину называют потоком вектора напряжённости (ПВН) через площадку dS (к-рая характеризуется вектором n dS). ПВН - величина алгебраическая, т.е. зависит от выбора направления нормали, для замкнутых поверхностей за положит. направление принимается внешняя нормаль. Для переменных в пространстве полей поток ч/з поверхность s: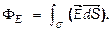

Закон Гаусса формулируется для сферы (рис.6), охватывающей точечный ЭЗ Q в центре, затем обобщается на замкнутую поверхность произвольной формы, заключающей внутри систему ЭЗ ( или объёмный заряд ). Поток вектора напряжённости сквозь замкнутую поверхность s выражается интегралом: 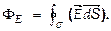Доказывается, что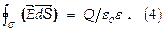

Закон (теорема) Гаусса (4) формулируется т.о.: поток вектора напряженности ЭСП сквозь замкнутую поверхность равен заряду, охватываемому этой поверхности, отнесенному к диэлектрической проницаемости среды, окружающей заряды. Физич. сущность закона в том, что линии ЭСП начинаются и заканчиваются на полюсах (зарядах, к-рые и являются источниками электрич. поля).

Проводники в электростатическом поле.

Проводниками называют вещества, способные проводить электрический ток. Для того, что бы вещество являлось проводником, оно должно содержать заряженные частицы, способные достаточно свободно передвигаться по объему проводника. Типичным представителем проводников являются металлы, носителями ЭЗ в них являются свободные электроны.

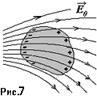
Внутренняя структура металлов, представляет собой кристаллич. решетку, образованную положительно заряженными ионами. Электроны атомов металлов, находящиеся на высоких орбиталях, слабо связаны с ядром, при образовании кристалла отрываются от своего атома и м-т свободно передвигаться по объему всего кристалла, образуя своеобразное облако свободных электронов (их совокупность именуется электронным газом, и его поведение в теории проводимости рассматривается по аналогии с одноатомным газом). Суммарный ЭЗ проводника остается равным нулю, ЭП облака свободных электронов компенсируется полем положит. ионов кристаллич. решетки. Наличием этих свободных электронов обусловлены проводящие свойства металлов. При помещении металла в ЭП на свободные электроны действуют электрич. силы, под действием к-рых электроны приходят в движение. Если ЭП не слишком велико, то электроны не могут покинуть объем металла и скапливаются на одной стороне проводника ( рис .7), с другой стороны проводника образуется недостаток электронов, поэтому положительный заряд ионов решетки оказывается нескомпенсированным. Таким образом, на поверхности проводника появляются ЭЗ, при этом суммарный ЭЗ проводника остается неизменным.

Явление возникновения электрич. зарядов на поверхности проводнике под воздействием приложенного электрич. поля называется электростатической индукцией, а возникшие заряды – индуцированными. В условиях постоянного внешнего поля устанавливает равновесие между разделенными на поверхностях проводника положит. и отрицат. ЭЗ. Отметим, что напряженность электрического поля внутри проводника равна нулю: поск-ку между зарядами на поверхности внутри проводника также возникает поле обратного направления по отношению ко внешнему. Напряжённостью этого поля уравновешивается внешнее поле. Важно, что условия равновесия не изменяются, если проводнику сообщить избыточный ЭЗ, к-рый также перераспределится по поверхности проводника и также будет создавать в пространстве вокруг проводника ЭП.

Емкость. Итак, проводники обладают свойством накапливать избыточный ЭЗ. Естественно, что такой заряд ( напр-р, величины Q) создаёт в окружающем пространстве ЭП и его характеризуют потенциалом φ. Известно, что потенциал прямо пропорционален ЭЗ, однако, разные проводники с одинаковым зарядом Q могут иметь различный потенциал. Для уединенного проводника формально записывают 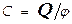и величину С называют емкостью.

физический смысл этой величины определяют как заряд, сообщение к-рого проводнику изменяет его потенциал на единицу 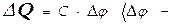здесь приращение потенциала). Емкость не зависит от заряда проводника и его потенциала, от материала и формы проводника, и единицей измерения имеет фарад (Ф) - на практике используются дольные единицы. Для шара радиуса R и обладающего ЭЗ Q нетрудно показать, что

На практике используются такие устройства как конденсаторы - 2 проводящих поверхности - обкладки на расстоянии d с площадью S (рис. 8). Из-за ЭС индукции на ближайшей поверхности обкладки создается заряд противоположного знака, к-рый понижает потенциал другой обкладки, создавая возможность повышения итоговой емкости: Здесь 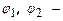потенциалы обкладок, здесь 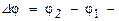разность потенциалов на обкладках. Особенностью конденсатора является то, что ЭСП между обкладками м-но считать однородным (т.е., с напряжённостью, не зависящей от координат), и поэтому разность потенциалов связана с напряжённостью линейно 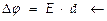здесь

Формула для емкости плоского конденсатора получается на основе определения емкости при учете однородного характера ЭП (Е ₁ - напряженность, создаваемая ЭЗ одной из обкладок) и с привлечением формулы для напряженности, создаваемой равномерно заряжённой плоскостью (Е ₁ =

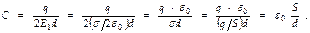
Энергия ЭСП заключена в объёме конденсатора 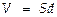и связана с разностью потенциалов При перемещении ЭЗ d q в поле между обкладками выполняется элементарная работа – d A = Dj× d q = q ×d q /C ® A = q ²/2C (полная работа при зарядке находится интегрированием в пределах от 0 до 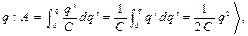тогда также для энергии заряжённого конденсатора (энергия равна работе, выполненной при зарядке конденсатора) также запишем также с учетом того, что 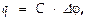получаем 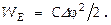Плотность энергии ЭСП в конденсаторе выражается как 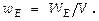Поск-ку а ёмкость конденсатора с пластиной диэлектрика проницаемости e между обкладками для плотности ЭСП внутри конденсатора получаем выражение Формула для плотности ЭСП применима для определения плотности энергии электрич. поля.