Лабораторная работа №3
Изучение магнитного поля (закон Био-Савара-Лапласа)
ВЫПОЛНИЛА: студентка гр. ИЗ-10-2 ______________ / Прохина А.Д./
ПРОВЕРИЛ: ______________ / Левин К.Л./
Санкт-Петербург
Цель работы: Измерение магнитных полей, создаваемых проводниками различных конфигураций. Экспериментальная проверка закона Био–Савара–Лапласа.
Краткое теоретическое содержание .
1 ) Магнитное поле прямолинейного проводника с током
Проводник, по которому протекает электрический ток, создает магнитное поле. Магнитное поле характеризуется вектором напряженности `H (рис. 1), который можно вычислить по формуле
`H = òd `H.
Cогласно закону Био-Савара-Лапласа,
,
где I – сила тока в проводнике, d ` l – вектор, имеющий длину элементарного отрезка проводника и направленный по направлению тока, `r – радиус вектор, соединяющий элемент с рассматриваемой точкой P.
Рассмотрим магнитное поле, создаваемое прямолинейным проводником с током конечной длины (рис. 2).
Получим формулу
.
Учитывая, что в настоящей работе длина проводника 2 b много больше расстояния r 0 от проводника до точки наблюдения магнитного поля, формулу (3) можно записать в виде
.
Поэтому индукция магнитного поля рассчитывается по формуле:
,
где m 0 – магнитная постоянная, m – магнитная проницаемость среды (для воздуха m = 1)
2) Магнитное поле на оси короткой катушки с током
Короткая катушка – цилиндрическая проволочная катушка, состоящая из N витков одинакового радиуса. Из-за осевой симметрии и в соответствии с принципом суперпозиции магнитное поле такой катушки на оси H представляет собой алгебраическую сумму полей отдельных витков H i: 
. Таким образом, магнитное поле короткой катушки, содержащей N к витков, в произвольной точке оси рассчитывается по формулам
, 
,
где H – напряженность, B – индукция магнитного поля.
3) Магнитное поле соленоида с током
Для расчета индукции магнитного поля в соленоиде используется теорема о циркуляции вектора магнитной индукции:
,
где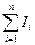 
– алгебраическая сумма токов, охватываемых контуром L произвольной формы, n – число проводников с токами, охватываемых контуром
Применим теорему о циркуляции вектора магнитной индукции к соленоиду, длиной l, имеющим N с витков с силой тока I. В расчете учтем, что практически всё поле сосредоточено внутри соленоида (краевыми эффектами пренебрегаем) и оно является однородным. Тогда формула примет вид:
,
откуда находим индукцию магнитного поля, создаваемую током внутри соленоида:
 |
Рис. 3. Соленоид с током и его магнитное пол
Схема установки
Рис. 4 Принципиальная электрическая схема установки
1 – измеритель индукции магнитного поля (тесламетр), А – амперметр, 2 – соединительный провод, 3 – измерительный щуп, 4 – датчик Холла*, 5 – исследуемый объект (короткая катушка, прямой проводник, соленоид), 6 – источник тока, 7 – линейка для фиксирования положения датчика, 8 – держатель щупа.
Расчетные формулы
, ,
где H – напряженность, B – индукция магнитного поля короткой катушки содержащей N витков.
Где В – индукция магнитного поля, создаваемая потоком внутри соленоида.
,
где m 0 – магнитная постоянная, m – магнитная проницаемость среды (для воздуха m = 1),
В – индукция магнитного поля прямолинейного проводника
где Y – потокосцепление,
Y = NсBS,
где В – магнитная индукция в соленоиде
S = p d 2/4 – площадь сечения соленоида.
Таблицы с результатами измерений и вычислений.
Таблица 1 Зависимость магнитной индукции на оси короткой катушки от расстояния до центра катушки
| z | см | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | ||
| Bэксп | мТл | 0,19 | 0,18 | 0,17 | 0,16 | 0,14 | 0,11 | 0,06 | 0,02 | 0,00 | |
| B теор | мТл | 0,188 | 0,182 | 0,174 | 0,158 | 0,142 | 0,106 | 0,067 | 0,019 | 0,004 |
| z | см | ||||||||
| Bэксп | мТл | 0,03 | 0,09 | 0,14 | 0,16 | 0,18 | 0,2 | 0,21 | 0,22 |
| B теор | мТл | 0,032 | 0,087 | 0,143 | 0,165 | 0,181 | 0,21 | 0,22 | 0,23 |
Таблица2 Зависимость магнитной индукции в центре короткой катушки от силы тока в ней
| I | A | 0,5 | 1,5 | 2,5 | 3,5 | ||||
| Bэксп | мТл | 0,05 | 0,07 | 0,09 | 0,11 | 0,13 | 0,14 | 0,16 | |
| B теор | мТл | 0,04 | 0,065 | 0,087 | 0,101 | 0,126 | 0,139 | 0,162 |
| I | A | 4,5 | ||
| Bэксп | мТл | 0,17 | 0,19 | 0,21 |
| B теор | мТл | 0,17 | 0,20 | 0,24 |
Таблица3 Зависимость магнитной индукции на оси соленоида от расстояния до его центра
| z | см | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | |
| Bэксп | мТл | 1,62 | 1,53 | 1,28 | 0,66 | 0,26 | 0,13 | 0,06 | 0,03 | 0,02 | 0,01 | |
| B теор | мТл | 1,64 | 1,52 | 1,30 | 0,72 | 0,33 | 0,15 | 0,05 | 0,04 | 0,03 | 0,01 | 0,003 |
| z | см | ||||||||||
| Bэксп | мТл | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,07 | 0,15 | 0,4 | 0,98 | 1,43 |
| B теор | мТл | 0,01 | 0,02 | 0,027 | 0,036 | 0,049 | 0,067 | 0,144 | 0,42 | 0,99 | 1,45 |
Таблица4 Зависимость магнитной индукции в центре соленоида от силы тока в нем
| I | A | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | ||||||
| Bэксп | мТл | 0,41 | 0,57 | 0,69 | 0,83 | 0,97 | 1,11 | 1,26 | 1,41 | 1,53 | 1,67 | |
| B теор | мТл | 0,43 | 0,54 | 0,65 | 0,85 | 0,93 | 1,102 | 1,21 | 1,39 | 1,51 | 1,63 | |
| мкГн |
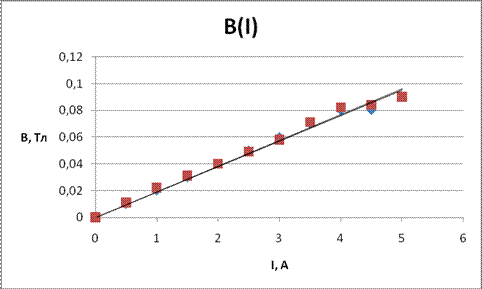
Таблица5 Зависимость магнитной индукции, создаваемой прямолинейным проводником, от силы тока в нем
| I | A | 0,5 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | ||
| Bэксп | мТл | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | |
| B теор | мТл | 0,011 | 0,022 | 0,031 | 0,04 | 0,049 | 0,058 | 0,071 | 0,082 | |
| r 0 | мкм | 3,33 |
| I | A | 4,5 | 5,0 |
| Bэксп | мТл | 0,08 | 0,09 |
| B теор | мТл | 0,084 | 0,09 |
| r 0 | мкм | 3,33 |
Таблица 6 Параметры исследуемых образцов
| N | R | N | d | l | L |
| 0,03(м) | 26*10-5(м) | 20*10-2(м) |
Примеры расчетов:
Магнитная индукция короткой катушки:
Магнитная индукция соленоида:
Площадь поперечного сечения проводника:
Потокосцепление:
Индуктивность:
Кратчайшее расстояние от датчика до проводника с током:
Погрешности косвенных измерений:
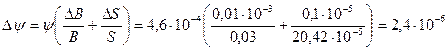
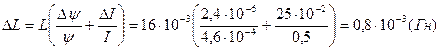
Графики теоретической и экспериментальной зависимости:
Теоретическая и экспериментальная зависимости магнитной индукции короткой катушки от силы тока:
Теоретическая и экспериментальная зависимости магнитной индукции в центре соленоида от силы тока:
Теоретическая и экспериментальная зависимости магнитной индукции проводника от силы тока:
