Найбільш повний опис особливостей структурного складу і механічної поведінки композиційних матеріалів можливе на основі статистичного підходу.
Для двокомпонентних композиційних матеріалів (N = 2) трансверсальних модулі пружності ізотропного виду обчислюють за нижчеперелічених формулами:
 (1)
(1)
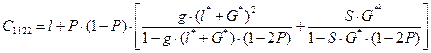 (2)
(2)
 (3)
(3)
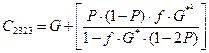 (4)
(4)
 (5)
(5)
де
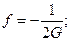


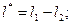

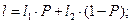
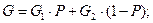



Р- об'ємний вміст другого компонента (армуючого компонента);
 - модулі зсуву першого і другого компонентів композиційного матеріалу відповідно;
- модулі зсуву першого і другого компонентів композиційного матеріалу відповідно;
 - об'ємні модулі пружності першого та другого компонентів композиційного матеріалу відповідно.
- об'ємні модулі пружності першого та другого компонентів композиційного матеріалу відповідно.
Технічні пружні постійні визначаються як
 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
Для ізотропних композиційних матеріалів з хаотичним розташуванням армуючого компонента за обсягом матеріалу пружні характеристики обчислюються:
 (10)
(10)
 (11)
(11)
 .(12)
.(12)
Організація обчислювального процессу
Обчислювальний процес, пов'язаний з визначенням фізико-механічних характеристик композиційних матеріалів, організують відповідно до алгоритму, блок-схема якого наведена на рис 1.
Блок схема алгоритму розрахунку механічних і теплофізичних параметрів вуглецевих матеріалів.



Програма набору для Turbo Pascal
Умовні позначення для введення символів в Turbo Pascal:

Програма вводу:
Program kursovoj;
Var K, K1, G1, K2, G2, Pn, Pk, P, l1, l2, G, l, lz, Gz, S, q, f, C11, C12, C13, C33, C44, KM, GM, G12, G13, EM, E1, E3: real; f1: text;
Label M1;
begin
assign (f1; ‘res1.pas’);
rewrite (f1);
write (‘vvedite K1, G1, K2, G2, Pn, Pk’);
read (K1, G1, K2, G2, Pn, Pk);
P:=Pn;
M1:
K:= K1*P+K2*(1-P);
l1:= K1+(2/3)*G1;
l2:= K2-(2/3)*G1;
G:=G1*P+G2*(1-P);
l:= l1*P+L2*(1-P);
Gz:= G1-G2;*
lz:= l1-l2;
S:= -(l+3*G)/(2*G*(l+2*G));
q:= -1/(l+2*G);
f:=1/(2*G);
C11:= l+2*G+P*(-1*P)*(q*l2+G2)/(1-q*(lz+Gz)*(1-2*P))+(S*lz*lz)/(1-S*Gz*(1-2*P));
C12:= l+P*(1-P)*((q*sqr(lz+Gz)/(1-q*(lz+Gz)*(1-2*P))+(S*Gz*Gz)/(1-S*Gz*(1-2*P)));
C13:= l+((P*(1-P)*q*lz*(lz+Gz))/(1-q*(lz+Gz)*(1-2*P)));
C44:= G+((P*(1-P)*f*Gz*Gz)/1-f*Gz*(1-2*P)));
C33:= l+2*G+((P*(1-P)*q*lz*lz)/(1-q*lz+Gz)*(1-2*P)));
E1:= ((C33*(C11+C12)-2*C13*C13)*(C11-C12)/(C33*C11-(C13*C13)));
E3:= ((C33*(C11+C12)-2*C13*C13))/(C11+C12));
G12:=(1/2)*(C11-C12);
G13:= C44;
Write(‘E1=’, E1, ‘E3=’, E3, ’G12=’, G12, ‘G13=’, G13);
GM:= G-((2*G*G*(K+2*G)*P*(1-P))/(5*G*(K+(4/3)*G)+2*Gz*(K+2*G)*(1-2*P)));
KM:= (K1*K2+(4/3)*G*K)/(K1*(1-P)+K2*P-(4/3)*G);
EM:= (q*KM*GM)/((3*KM)+GM);
Writeln (f1, ‘GM=’, GM, ‘KM=’, KM, ‘EM=’, EM);
P: =P+0.1
If P=0.5 then P:= P+0.1;
If P<= Pk then goto M1
end.
Індивідуальне завдання
Механічні та теплофізичні характеристики армуючих елементів і матричного матеріалу
| Армуючий компонент | Матричний компонент | ||
 , ГПа , ГПа
|  ,ГПа ,ГПа
|  ,ГПа ,ГПа
|  ,ГПа ,ГПа
|
| 13,2 | 21,9 |
Після введення програми в Turbo Pascal ми отримуємо такі результати:

| 0,3 | 0,4 | 0,6 | 0,7 |
 
| 397,6 | 527,0 | 669,0 | 648,9 |
| 1127,4 | 1486,9 | 2202,2 | 2555,7 |

| 913,1 | 1105,9 | 1248,6 | 1163,8 |

| 2163,4 | 1391,3 | 1365,9 | 1447,6 |
| 511,5 | 649,5 | 907,5 | 1049,7 |

| 1743,1 | -2870,4 | -1255,1 | -1208,7 |

| -0,137 | 0,157 | -0,180 | -0,192 |
З отриманих результатів будуємо графік залежності модулів пружності, коефіцієнтів теплопровідності і коефіцієнтів лінійного термічного розширення в залежності від об'ємного вмісту Р армуючого компонента.
Рис. 1

Рис.2

Висновок
При курсовому проектуванні побудували графіка залежності модулів пружності, коефіцієнтів теплопровідності і коефіцієнтів лінійного термічного розширення в залежності від об'ємного вмісту армуючого компонента Р. Р змінювалася від 0,3 до 0,7.
Звернули увагу що при збільшенні об'ємного вмісту армуючого компонента Р технічні пружні постійні =, теж збільшуються. Зворотну залежність спостерігаємо у G.А для ізотропних матеріалів з хаотичним розташуванням армуючого компонента за об'ємом збільшується, має складну залежність з екстремумами, а залишається практично незмінною.
Вивчивши графіки можна зробити висновок що найбільш оптимальне значення Р = 0,6, тоді у більшості технічних характеристик спостерігається максимуми.
Литература
1. Волков С.Д., Ставров В.П. Статична механіка композитних матеріалів
Мінська БГУ, 1978 - 205 с.
2. Соколкін Ю.В. Ташкінов А.А. Механіка деформування і руйнування
структурно неоднорідних тел. М. Наука.1984 - 114 с.
3. Соколкін Ю.В., Скачков В.О., Танакеева М. Г. Леонтьєв В.А.Дослідження
процесів деформування і руйнування композитних матеріалів і
конструкцій
при складному навантаженні / Механіка конструкцій з композитних
матеріалів. - К.: Наука, 1984 - с. 97-107.
4.Шермергор Т.Д. Теорія пружності мікронеоднорідних середовищ. - М:
5.Наука, 1997 - 398 с.






