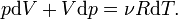Здесь — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а

Частные случаи

1. Если , то это означает, что тепло к системе подводится.

2. Если , аналогично — тепло отводится.

3. Если , то система не обменивается теплом с окружающей средой и называется адиабатически изолированной.

Первое начало термодинамики:

· при изобарном процессе

· при изохорном процессе ()

· при изотермическом процессе

Здесь 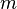— масса газа, — молярная масса газа, — молярная теплоёмкость при постоянном объёме, — давление, объём и температура газа соответственно, причём последнее равенство верно только для идеального газа.

Адиабатический процесс - термодинамический процесс, при котором система не обменивается тепловой энергией с окружающим пространством. [кароч: при этом процессе ТЕПЛООБМЕНА НЕТ (Q=0) ]

Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной и изменения энтропии не происходит.

Первое начало термодинамики для адиабатического процесса:

где — изменение внутренней энергии тела, 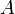— работа, совершаемая системой.

где — его объём, — показатель адиабаты, и — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.

С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду

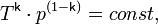
где 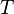— абсолютная температура газа. Или к виду

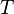Поскольку всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении ) газ нагревается ( возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент .

Вывод уравнения

Согласно закону Менделеева — Клапейрона для идеального газа справедливо соотношение

где R — универсальная газовая постоянная. Вычисляя полные дифференциалы от обоих частей уравнения, полагая независимыми термодинамическими переменными , получаем

(3)

или, введя коэффициент :

Это уравнение можно переписать в виде

что после интегрирования даёт:

Потенцируя, получаем окончательно:

что и является уравнением адиабатического процесса для идеального газа.

Теорема Гаусса

Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью

Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

Интегральная форма:

где

· — поток вектора напряжённости электрического поля через замкнутую поверхность .

· — полный заряд, содержащийся в объёме, который ограничивает поверхность .

· — электрическая постоянная.

Дифференциальная форма:

Здесь — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а — оператор набла.