Берілгені: 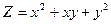 табу керек:
табу керек: 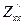 А) 2В) 4/2С) 6/3
А) 2В) 4/2С) 6/3
Берілгені:  . Нүктесіндегі
. Нүктесіндегі  мәнін табыңыз: C)4 D)
мәнін табыңыз: C)4 D)  G)
G) 
Берілгені: 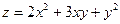 . Нүктесіндегі
. Нүктесіндегі 
 -ті табыңыз: A)
-ті табыңыз: A)  D)
D)  F)
F) 
Берілгені:  . Табу керек:
. Табу керек: 
 А) 24/2В) 12
А) 24/2В) 12
Берілгені:  . Табу керек:
. Табу керек:  - А)
- А)  В) -3
В) -3
Берілгені:  . Табыңыз:
. Табыңыз: 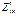 A) 12 C)24/2 D)36/3
A) 12 C)24/2 D)36/3
Берілгені:  . Табыңыз:
. Табыңыз:  A)4 C)
A)4 C)  F)
F) 
Берілгені:. Табыңыз: D)-3 E)- H)-6/2
Берілгені:.Табыңыз:.А) -40 E)-80/2 H)-120/3
Берілгені: А= 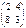 , В=
, В=  . Берiлген матрицалардың көбейтіндісін тап. A)
. Берiлген матрицалардың көбейтіндісін тап. A)  C)
C)  F)
F) 
Берілгені: А=  , В=
, В=  . Берiлген матрицалардың көбейтіндісін тап. A)
. Берiлген матрицалардың көбейтіндісін тап. A)  C)
C)  F)
F) 
Берілгені: А=  . Берiлген матрицаның А2 тап. A)
. Берiлген матрицаның А2 тап. A)  B)
B)  C)
C) 
Берілгені: А=  . Берiлген матрицаның А2 тап. A)
. Берiлген матрицаның А2 тап. A) 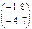 B)
B) 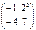 C)
C) 
Берілгені:  табу керек:
табу керек:  А) 12В) 36/3С) 24/2
А) 12В) 36/3С) 24/2
Берілгені:  табу керек:
табу керек: 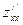 А) 4/2В) 2С) 6/3
А) 4/2В) 2С) 6/3
Берілгені:  табу керк
табу керк  : С) 24/2D) 12
: С) 24/2D) 12
Берілгені:  табу керек:
табу керек:  A)4\2C)6\3D)2
A)4\2C)6\3D)2
Бірінші ретті сызықтық дифференциалдық теңдеу: B)  C)
C) 
Бірінші ретті сызықтық дифференциалдық теңдеу: В)  С)
С) 
Бірінші ретті сызықтық дифферециалдық теңдеу: А)  / В)
/ В) 
В) 2/10
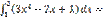 В) бүтін сан
В) бүтін сан
Векторлардың компланарлық шарты: A)осы векторлардан құрылған параллелепипедтің көлемі кез –келген оң санға теңC) осы векторлардан құрылған параллелепипедтің көлемі 1-ге теңF)осы векторлардан құрылған пирамиданың көлемі 1-ге тең
Векторлардың компланарлық шарты: А) осы векторлардан құрылған параллелипедтің көлемі кез-келген оң санға теңС) осы векторлардан құрылған параллелипедтің көлемі 1-ге теңЖ) осы векторлардан құрылған пирамиданың көлемі 1-ге тең
 векторының модулiн тап. B)
векторының модулiн тап. B)  D)
D) 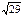 E)
E) 
 векторының модулін тап А) 2
векторының модулін тап А) 2
Векторының ұзындығын табыңдар.B)13 D)26/2 H)39/3
Гармоникалық қатардың түрі: A)  E)
E)  G)
G) 
Д) 3/10
Даламбер белгісі бойынша қатар  : С)жинақты,өйткені
: С)жинақты,өйткені  E)жинақты
E)жинақты
Даламбер белгісі бойынша қатар  А) жинақтыВ) жинақты, өйткені
А) жинақтыВ) жинақты, өйткені 
Даламбер белгісі бойынша қатар 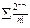 А) жинақты, өйткені
А) жинақты, өйткені  В) жинақты
В) жинақты
Дәрежелік қатардың  жалпы мүшесі келесі өрнек болады: A)
жалпы мүшесі келесі өрнек болады: A)  C)
C)  G)
G) 
Дәрежелік қатардың  жалпы мүшесінің коэффициенті теңA)
жалпы мүшесінің коэффициенті теңA)  G)
G)  H)
H) 
Дәрежелік қатардың  жалпы мүшесі келесі функция болады: D)
жалпы мүшесі келесі функция болады: D)  G)
G)  H)
H) 
 дәрежелік қатарының жинақтылық радиусын тең: A)
дәрежелік қатарының жинақтылық радиусын тең: A) 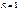 C)
C)  E)
E) 
Дисперсия 1/36 - ке тең болса, онда орташа квадраттық ауытқуды табыңыз. B)1/6 E) 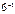 G)1/
G)1/ 
 дифференциалдық теңдеуінің реті тең: D)4 F)
дифференциалдық теңдеуінің реті тең: D)4 F)  H)
H) 
Е) 1/10
Егер болса, табу керек: C)2 E)4/2 H)6/3
Егер  функциясы біртекті болса, онда оның біртектілік дәрежесін табу керек: B)
функциясы біртекті болса, онда оның біртектілік дәрежесін табу керек: B)  C) 0
C) 0
Егер  берілген болса, онда
берілген болса, онда  кездейсоқ шаманың математикалық үмітін табыңыз. B)3 F)
кездейсоқ шаманың математикалық үмітін табыңыз. B)3 F) 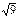 H)
H) 
Егер  берілген болса, онда
берілген болса, онда  кездейсоқ шаманың математикалық үмітін табыңыз. A)-4 D)-8/2 G)-12/3
кездейсоқ шаманың математикалық үмітін табыңыз. A)-4 D)-8/2 G)-12/3
Егер болса, табу керек: A)8/3 C)16/6 E)24/9
Егер болса, табу керек: B)3 D)6/2 G)9/3
Егер болса, табу керек: A) 2/9 D)4/18 G)6/27
Егер болса, у¢(1) табу керек: B)5 E)15/3 G)10/2
Егер функциясы біртекті болса, онда оның біртектілік дәрежесін анықтаңыз. B)0 D) F)0/2
Егер  функциясы біртекті болса, онда оның біртектілік дәрежесін анықтаңыз. B)0 D)
функциясы біртекті болса, онда оның біртектілік дәрежесін анықтаңыз. B)0 D)  E)3
E)3
Егер  функциясы біртекті болса, онда оның біртектілік дәрежесін табу керек: А) 0В)
функциясы біртекті болса, онда оның біртектілік дәрежесін табу керек: А) 0В) 
Егер f(x) =  болса,
болса,  табу керек:A) 0 C)0/9 G)0/6
табу керек:A) 0 C)0/9 G)0/6






