Математика
 анықталмаған интеграл тең: A)
анықталмаған интеграл тең: A) 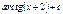 C)
C) 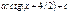 E)
E) 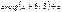
 берілген гиперболаның эксцентриситетін тап: A)
берілген гиперболаның эксцентриситетін тап: A) 
 - де
- де  функциясының ең үлкен мәнін табыңдар: А) 160 / В) 320/2
функциясының ең үлкен мәнін табыңдар: А) 160 / В) 320/2

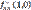 дербес туындысы: A) 0 E) нақты сан
дербес туындысы: A) 0 E) нақты сан
 және
және  түзулері: B)
түзулері: B)  бұрыш жасайдыE) перпендикуляр
бұрыш жасайдыE) перпендикуляр
 қатарының бесінші мүшесі: D)4 F)
қатарының бесінші мүшесі: D)4 F)  G)Оң сан
G)Оң сан
 - нің ќандай мәнінде қандай төмендегі екі жазықтықтың біріне - бірі перпендикуляр болады:
- нің ќандай мәнінде қандай төмендегі екі жазықтықтың біріне - бірі перпендикуляр болады:  A) 36 В)
A) 36 В)  С)
С) 
 - нің қандай мәнінде қандай төмендегі екі жазықтықтың біріне - бірі перпендикуляр болады:
- нің қандай мәнінде қандай төмендегі екі жазықтықтың біріне - бірі перпендикуляр болады:  A) 36 D)
A) 36 D)  G)
G) 
 - нің қандай мәнінде төмендегі екі жазқтықтың біріне - бірі перпендикуляр болады:
- нің қандай мәнінде төмендегі екі жазқтықтың біріне - бірі перпендикуляр болады:  ,
,  . А) 5 В)10/2 С)
. А) 5 В)10/2 С) 
 уневерсал ауыстырып қолдану арқылы табылатын интеграл: B)
уневерсал ауыстырып қолдану арқылы табылатын интеграл: B)  C)
C)  E)
E) 
 ,
,  . А+В матрицасын табу керек: А)
. А+В матрицасын табу керек: А)  D)
D) 
Векторлардың скаляр көбейтіндісін табыңдар.A) -9 C)-18/2 H)-27/3
 =
=  векторының модулін тап: B)
векторының модулін тап: B)  C)
C) 
 =: B)
=: B) 
 айқын емес функциясы үшін
айқын емес функциясы үшін  дербес туындысы А) -1В) теріс сан
дербес туындысы А) -1В) теріс сан
 айқын емес функциясы үшін
айқын емес функциясы үшін  дербес туындысы: А) бүтін санВ) 2
дербес туындысы: А) бүтін санВ) 2
 анықталған интеграл тең A) 1/4 B)0,25 D)2/8
анықталған интеграл тең A) 1/4 B)0,25 D)2/8
 анықталған интеграл тең. A) 1/5 B)0,2 E)3/15
анықталған интеграл тең. A) 1/5 B)0,2 E)3/15
 анықталған интеграл тең: A)
анықталған интеграл тең: A)  B)
B)  C)
C) 
 анықталмаған интегралы тең: A)
анықталмаған интегралы тең: A)  B)
B)  D)
D) 
 берілген эллипстің эксцентриситетін тап: А) 0,8Ж) 8/10
берілген эллипстің эксцентриситетін тап: А) 0,8Ж) 8/10
 берілген эллипстің эксцентриситетін тап: E) 0,8 F) 8/10
берілген эллипстің эксцентриситетін тап: E) 0,8 F) 8/10
 болғанда
болғанда  функциясының туындысы
функциясының туындысы  тең: A)8 D)
тең: A)8 D)  G)
G) 
Векторлардың скаляр көбейтіндісін табыңдар.D)-3 G) H)-9/3
 векторларынан ќұралған параллелограмның ауданы: А)2 В)4/2 С)6/3
векторларынан ќұралған параллелограмның ауданы: А)2 В)4/2 С)6/3
 векторларынан құралған параллелограмның ауданы: C)2 E)4/2 H)6/3
векторларынан құралған параллелограмның ауданы: C)2 E)4/2 H)6/3
Векторларының скаляр көбейтiндiсiн тапB)8 E)16/2 H)24/3
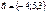 векторының модулiн тап. A)
векторының модулiн тап. A)  C)
C)  H)
H) 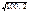
 векторының модулін тап: А)
векторының модулін тап: А) 
 векторының модулін тап: A)
векторының модулін тап: A) 
 векторының модулін тап: А)
векторының модулін тап: А)  В)
В) 
 векторының модулін тап А)
векторының модулін тап А)  В)
В) 
 векторының ұзындығы тең А) 2В)
векторының ұзындығы тең А) 2В)  С)
С) 
Векторының ұзындығын табыңдар. A) 7 D)14/2 G)28/4
Векторының ұзындығын табыңдар. A)11 B)33/3 C)66/6
Векторының ұзындығын табыңдар. C)14D)28/2 E)42/3
Векторының ұзындығын табыңдар. C)25 E)50/2 H)75/3
Векторының ұзындығын табыңдар.A) 5 C)10/2 G)20/4
Векторының ұзындығын табыңдар.A) 7 D)14/2 G)28/4
 векторының ұзындығын табыңдар. A )6 B)
векторының ұзындығын табыңдар. A )6 B)  C)
C) 
Векторының ұзындығын табыңдар.B)13 D)26/2 H)39/3
 векторының ұзындыєын табыңдар. А)6 В)
векторының ұзындыєын табыңдар. А)6 В)  С)
С) 
 гиперболоиды: А) бірдей жарты өстермен / В)
гиперболоиды: А) бірдей жарты өстермен / В)  өсі бойымен созылған / Д) бір қуысты
өсі бойымен созылған / Д) бір қуысты
 гиперболоиды А)
гиперболоиды А)  нүктесі арқылы өтедіВ) бірдей жарты өстермен С) оz өсі бойымен созылған
нүктесі арқылы өтедіВ) бірдей жарты өстермен С) оz өсі бойымен созылған
Дәрежелік қатарының жинақтылық радиусы тең: D)1 G)2/2 H)8/8
 дәрежелік қатарының жинақтылық радиусын табыңыз: C)
дәрежелік қатарының жинақтылық радиусын табыңыз: C)  D)
D)  G)
G) 
 дифференциалдық теңдеуін шешіңіз: D)
дифференциалдық теңдеуін шешіңіз: D)  G)
G)  H)
H) 
 дифференциалдық теңдеуінің реті тең: A)1 C)
дифференциалдық теңдеуінің реті тең: A)1 C)  E)
E) 
 дифференциалдық теңдеуінің реті тең: A)1 C)
дифференциалдық теңдеуінің реті тең: A)1 C)  E)
E) 
 дифференциалдық теңдеуінің реті тең: D)3 E)
дифференциалдық теңдеуінің реті тең: D)3 E) 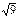 G)
G) 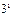
 дифференциалдық теңдеуінің шешімін табыңыз B)
дифференциалдық теңдеуінің шешімін табыңыз B)  E)
E)  G)
G) 
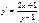 дифференциалдық теңдеуінің шешімін табыңыз B)
дифференциалдық теңдеуінің шешімін табыңыз B)  D)
D)  E)
E) 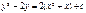
 дифференциалдық теңдеуінің шешімін табыңыз: A)
дифференциалдық теңдеуінің шешімін табыңыз: A)  D)
D)  E)
E) 
 дифференциалдық теңдеуінің шешімін табыңыз: A)
дифференциалдық теңдеуінің шешімін табыңыз: A)  F)
F)  G)
G) 
 дифференциалдық теңдеуінің шешімін табыңыз: D)
дифференциалдық теңдеуінің шешімін табыңыз: D)  E)
E)  H)
H) 
Екi нүктенiң арақашықтығын тап.A)5 C)10/2 H)15/3
Есептеңіз:A) ½ B) C) 0,5
Есептеңіз:E) 8/3 G) /3 H) 16/6
 жазықтығы: А) Ох өсінен 2-ге тең кесінді қияды В) Оу өсінен 3-ке тең кесінді қиядыД) Ох өсінен 2-ге тең кесінді қияды
жазықтығы: А) Ох өсінен 2-ге тең кесінді қияды В) Оу өсінен 3-ке тең кесінді қиядыД) Ох өсінен 2-ге тең кесінді қияды
 жазықтығында жатқан нүкте А)
жазықтығында жатқан нүкте А) 
 және
және  векторларының векторлық көбейтіндісі деп төмендегі шарттарды қанағаттандыратын
векторларының векторлық көбейтіндісі деп төмендегі шарттарды қанағаттандыратын  векторларын атайды: B)
векторларын атайды: B)  векторына да,
векторына да,  векторына да перпендикулярF) ұзындығы
векторына да перпендикулярF) ұзындығы  және
және  векторларынан құрылған паралелограммның ауданына теңG) осы векторлармен реттелген оң үштік құрайды
векторларынан құрылған паралелограммның ауданына теңG) осы векторлармен реттелген оң үштік құрайды
 және
және 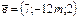 векторлары m - нің қай мәнінде перпендикуляр болады?: А)2 В)
векторлары m - нің қай мәнінде перпендикуляр болады?: А)2 В)  С)
С) 
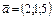 және
және  векторлары m - нің қай мәнінде перпендикуляр болады?:B)2 D)
векторлары m - нің қай мәнінде перпендикуляр болады?:B)2 D)  E)
E) 
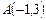 және
және  нүктелері арқылы өтетін түзудің теңдеуі: А)
нүктелері арқылы өтетін түзудің теңдеуі: А) 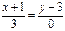 В)
В)  Е)
Е) 
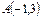 және
және  нүктелері арқылы өтетін түзудің теңдеуі Е)
нүктелері арқылы өтетін түзудің теңдеуі Е) 
 және
және  нүктелері берілген.
нүктелері берілген.  векторының ұзындығы: А) 5В) бүтін сан
векторының ұзындығы: А) 5В) бүтін сан
 және
және  нүктелері берілген.
нүктелері берілген.  кесіндісінің ортасының абсциссасы А) оң санС)3,5
кесіндісінің ортасының абсциссасы А) оң санС)3,5
 және
және 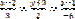 түзулері: D) параллельE)
түзулері: D) параллельE) 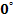 бұрыш жасайдыF)
бұрыш жасайдыF)  бағыттаушы векторына ие
бағыттаушы векторына ие
 және
және  түзулері: А) параллельВ)
түзулері: А) параллельВ)  бағыттаушы векторына ие
бағыттаушы векторына ие
 және
және  түзулері: В)
түзулері: В) 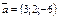 бағыттаушы векторына иеС) параллель Е) 00 бұрыш жасайды
бағыттаушы векторына иеС) параллель Е) 00 бұрыш жасайды
 және
және  түзулерінің арасындағы бұрыш табу формуласын көрсетіңіз: A)
түзулерінің арасындағы бұрыш табу формуласын көрсетіңіз: A) 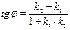 B)
B)  C)
C) 
 және
және  түзулерінің арасындағы бұрыш табу формуласын көрсетіңіз: А)
түзулерінің арасындағы бұрыш табу формуласын көрсетіңіз: А)  В)
В)  С)
С) 
 және
және 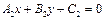 түзулерінің паралльлелдік шартын көрсетіңіз: А)
түзулерінің паралльлелдік шартын көрсетіңіз: А)  В)
В)  С)
С) 
 және
және  түзулерінің паралльлелдік шартын көрсетіңіз:A)
түзулерінің паралльлелдік шартын көрсетіңіз:A)  B)
B)  C)
C) 
 және
және  нүктелері берілген.
нүктелері берілген.  кесіндісінің ортасының ординатасы А) 0В) бүтін сан
кесіндісінің ортасының ординатасы А) 0В) бүтін сан
 және
және 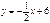 түзулері: А) перпендикулярВ) 900 бұрыш жасайды
түзулері: А) перпендикулярВ) 900 бұрыш жасайды
 интегралын есептеңіз: C)
интегралын есептеңіз: C) 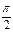 E)
E)  G)
G) 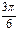
 интегралын есептеңіз: А)
интегралын есептеңіз: А)  G)
G)  H)
H) 
 интегралын табыңыз: C)
интегралын табыңыз: C)  E)
E)  H)
H) 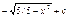
 интегралын табыңыз: A)
интегралын табыңыз: A)  C)
C)  E)
E) 
 интегралын табыңыз: D)
интегралын табыңыз: D)  G)
G)  H)
H) 
 интегралын табыңыз: D)
интегралын табыңыз: D)  G)
G) 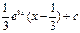 H)
H) 
 интегралын табыңыз: E)
интегралын табыңыз: E)  F)
F)  G)
G) 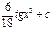
 интегралын табыңыз: A)
интегралын табыңыз: A)  C)
C)  F)
F) 
 комплекстік саны мынандай тригонометриялық түрде жазылады: A)
комплекстік саны мынандай тригонометриялық түрде жазылады: A)  B)
B)  E)
E) 
 Коши есебін шешіңіз: A)
Коши есебін шешіңіз: A)  E)
E)  H)
H) 
 қатарларының қайсысы жинақты қатар болады: A) 2 G)4/2 H)8/4
қатарларының қайсысы жинақты қатар болады: A) 2 G)4/2 H)8/4
 қатарының бесінші мүшесі А) оң санВ)
қатарының бесінші мүшесі А) оң санВ)  С) 4
С) 4
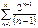 қатарының бесінші мүшесі: А) 4В)
қатарының бесінші мүшесі: А) 4В)  С) оң сан
С) оң сан
 қатарының тоғызыншы мүшесі А) рационал санВ) оң сан С) 9/82
қатарының тоғызыншы мүшесі А) рационал санВ) оң сан С) 9/82
 қатарының тоғызыншы мүшесі: А) рационал санВ) оң санЕ)
қатарының тоғызыншы мүшесі: А) рационал санВ) оң санЕ) 
 матрицасы берілген.
матрицасы берілген. 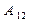 алгебралық толықтауышты есептеңіз: A) 6 В) 18/3 С) 12/2
алгебралық толықтауышты есептеңіз: A) 6 В) 18/3 С) 12/2
 матрицасының рангы: C) 1-ден артықD) 3G) 2-ден артық
матрицасының рангы: C) 1-ден артықD) 3G) 2-ден артық
 нүктесінде
нүктесінде  -нің мәні, егер
-нің мәні, егер  А) -1
А) -1
 нүктесінен
нүктесінен  түзуіне дейінгі қашықтық неге тең. A)3,5 D)7/2 G)35/10
түзуіне дейінгі қашықтық неге тең. A)3,5 D)7/2 G)35/10
 нүктесінен
нүктесінен  түзуіне дейінгі қашықтық неге тең. A)3,5 В)7/2 С)35/10
түзуіне дейінгі қашықтық неге тең. A)3,5 В)7/2 С)35/10
 нүктесінен
нүктесінен  түзуіне дейінгі қашықтықты табыңыз. A) 1 В)
түзуіне дейінгі қашықтықты табыңыз. A) 1 В)  С)
С) 
 нүктесінен
нүктесінен  түзуіне дейінгі қашықтықты табыңыз. A) 4 В)
түзуіне дейінгі қашықтықты табыңыз. A) 4 В)  С)
С) 
 параболасымен шектелген фигураның ауданын есептеңіз: A)
параболасымен шектелген фигураның ауданын есептеңіз: A)  D)
D)  G)
G) 
 сандық қатарының мүшелері: А)
сандық қатарының мүшелері: А)  В)
В)  Е)
Е) 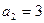
 Сандық қатарының мүшелері: C)
Сандық қатарының мүшелері: C)  D)
D)  E)
E) 
 сферасы үшін А)
сферасы үшін А) 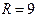 В) центрі
В) центрі  нүктедеС)
нүктедеС)  нүктесі сферада жатыр Ж) центрі
нүктесі сферада жатыр Ж) центрі 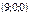 нүктеде
нүктеде
 сызық теңдеуінің
сызық теңдеуінің 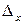 -ін есепте: А) -50 В) -100/2 С) -150/3
-ін есепте: А) -50 В) -100/2 С) -150/3
 сызықтық біртекті дифференциалдық теңдеуінің жалпы шешімін табыңыз: A)
сызықтық біртекті дифференциалдық теңдеуінің жалпы шешімін табыңыз: A)  C)
C)  G)
G) 
 сызықтық біртекті дифференциалдық теңдеуінің жалпы шешімін табыңыз. A)
сызықтық біртекті дифференциалдық теңдеуінің жалпы шешімін табыңыз. A)  C)
C)  F)
F) 
 сызықтық теңдеуінің
сызықтық теңдеуінің 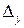 -ін есепте: А) -75 В)-300/4 С) -150/2
-ін есепте: А) -75 В)-300/4 С) -150/2
сызықтық теңдеуінің -ін есепте:A)-50 B)-100/2 C)-150/3






