Дисперсией света называется зависимость показателя преломления вещества от длины волны
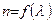. (7.1)
где 
- длина волны света в вакууме. Эта зависимость объясняется электронной теорией строения вещества и определяется инертностью электронов. Согласно этой теории молекулы представляют собой упругие структуры, которые под действием внешнего электромагнитного поля начинают колебаться и при этом испускают электромагнитные волны, что, в свою очередь, возбуждает следующие молекулы, заставляя в них колебаться электроны и так далее. В связи с этим, движение света в среде как бы замедляется, что и подтверждается при анализе волнового уравнения, где скорость света 
меньше скорости света в вакууме 
. где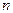 
- показатель преломления.
Для прозрачных тел, типа стекла, известна эмпирическая формула Коши
, (7.2)
где 
- некие коэффициенты.
Дифференцируя эту формулу по , получим 
, это говорит о том, что в таких материалах показатель преломления уменьшается при увеличении длины волны. Таким свойством обладают большинство материалов - это случай нормальной дисперсии. Однако встречаются ситуации, когда 
- это аномальная дисперсия. Согласно теории, в этом случае происходит резонансное поглощение электромагнитного поля молекулами вещества.
Явление дисперсии используется в некоторых спектральных приборах. В них
| 
|
основным элементом является дисперсионная призма, принцип действия которой базируется на законе Снеллиуса: угол преломления зависит от показателя преломления. Конструкция призмы выполнена таким образом, чтобы угловая дисперсия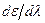 
была максимальна. Заметим, что угловая дисперсия положительна, т.е. большим длинам волн соответствует больший угол преломления 
, так как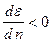 
в силу закона Снеллиуса, а 
из (7.2).
Однако во многих случаях дисперсия играет отрицательную роль. Известно, что для тонкой линзы фокусное расстояние 
определяется выражением
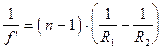, (7.3)
где 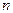- показатель преломления материала линзы, 
- радиусы кривизны первой и второй поверхности линзы соответственно. Так как 
, то и фокусное расстояние становится функцией длины волны. что приводит к нежелательному эффекту - хроматической аберрации, резко ухудшающего качество изображения. Ее устранение является одной из основных задач прикладной оптики.
Зависимость скорости распространения волны от и, следовательно, от частоты приводит к следующему. Пусть плоская волна 
имеет сложный состав по частотам. Тогда ее можно представить в виде ряда Фурье(7.4а), если она периодическая по 
или в виде интеграла Фурье (7.4б).
, (7.4а)
где 
; - длина волны в вакууме; 
- период колебаний световой волны.
, (7.4б)
где 
спектральная плотность. Эти выражения в сущности выражают одно и тоже: любая волна может представлена суммой одночастотных или монохроматических волн.
Если такая волна распространяется в вреде с дисперсией 
, то по прохождении дистанции 
(для простоты рассмотрим ряд Фурье) поле волны будет
(7.5)
и у каждой составляющей будет свой набег фазы
. (7.6)
Таким образом, спектральный состав электромагнитного поля, а следовательно, и само поле изменится. Из этого возникает о нетривиальности прохождении сигнала в диспергирующих средах и появляется неоднозначность определения скорости волны.
Следует отметить, что монохроматичных (одночастотных) волн в природе не бывает. Любая, ограниченная во времени волна, уже немонохроматична, а имеет некоторый спектральный состав. Например, излучение атома длится отрезок времени 
, тогда его спектр, т.е. распределение амплитуд по частотам будет
, (7.7)
где 
, если 
и 
, если 
, 
частота излучения атома. Вычисляя интеграл и воспользовавшись формулой Эйлера, получим
. (7.8)
График этой функции, т.е. спектр, будет иметь вид, показанный на рисунке. Такая электромагнитная волна называется квазимонохроматичной, так как она помимо основной частоты 
, содержит и набор частот в интервале 
, определяемом соотношением
, (7.9)
|
которое получается из условия того, что 
является первым корнем уравнения 
. В соответствии с изложенным, даже такая примитивная волна деформируется, пройдя диспергирующую среду.
Любая информация, передаваемая электромагнитном полем, в простейшем случае, это какая - то засечка на волне, что приведет к усложнению спектрального состава и по прохождении среды с дисперсией, такой сигнал изменится. В общем случае определить искажение волны достаточно сложно, поэтому для этого необходимо использовать некоторые упрощенные модели. С этой целью вводятся понятия фазовой и групповой скорости.
Известно, что уравнение плоской волны, распространяющейся вдоль оси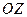 
(с учетом времени) имеет вид
. (7.10)
Отсюда уравнение поверхности равных фаз
. (7.11)
Скорость этой поверхности 
(из дифференциала (7.11) 
)
. (7.12)
Полученное выражение представляет собой скорость монохроматической волны или фазовая скорость.
Определим групповую скорость для простейшего случая суммы двух волн 
и 
с равной амплитудой.
, (7.13)
где 
Тогда, после преобразований (с использованием формулы Эйлера)
|
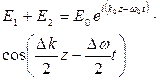.(7.14)
График этого сигнала показан на рисунке. Такого рода сигналы называются биениями. Они состоят из низкочастотной составляющей, в которой заключена полезная информация и высокочастотным заполнением. Перемещение информации характеризуется условием 
откуда скорость огибающей или скорость группы 
или в пределе
. (7.15)
Можно найти связь между фазовой и групповой скоростью. Так как 
, то
, но 
и 
, то окончательно
. (7.16)
Это формула Релея, которая связывает групповую и фазовую скорости через дисперсию среды. Из нее следует, что если дисперсия среды отсутствует, то скорость огибающей (информации) совпадает со скоростью распространения монохроматической волны, в противном случае они различны.
