Световые волны обладают большой частотой. Например, для длины волны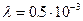 
мм, частота 
. Не существует устройств и не может существовать устройств, способных отрабатывать эту частоту. Все существующие приемники светового излучения усредняют принимаемый сигнал по времени, так как постоянная времени приемника 
много больше периода колебаний световой волны 
. По определению, среднее значение 
по времени (обозначается как 
) 
как
. (4.7)
Среднее значение напряженности поля 
(рассмотрим для определенности одну компоненту электрического поля)
, (4.8)
так как 
. Именно поэтому напряженность электромагнитного поля световой волны не может быть зарегистрирована.
Из курса физики известно, что плотности энергий электрического 
и магнитного 
полей, соответственно равны
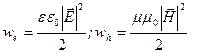. (4.9)
Среднее значение энергии
. (4.10)
Эта величина при 
отлична от нуля и может быть зарегистрирована.
. (4.11а)
По аналогии
. (4.11б)
Полная энергия электромагнитного поля
. (4.17)
Покажем, как определяется энергия электромагнитного поля, в случае представления его комплексными амплитудами. По определению
, (4.18)
где 
- комплексная амплитуда электрического поля (для магнитного 
). Известно, что для любого комплексного числа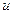 
. (4.18)
Тогда величина 
, необходимая для вычисления энергии 
будет
. (4.19)
При усреднении первое и третье слагаемые обратятся в нуль и окончательно
. (4.20)
Таким образом, для определения энергии необходимо взять квадрат модуля комплексной амплитуды, что дает большие удобства при вычислениях.
Поток энергии
Рассмотрим вопрос переноса энергии электромагнитной волной, исследуя уравнения Максвелла. Для получения необходимых соотношений, умножим первое уравнение (1.1) скалярно на 
, а (1.2) на 
, и сложим
Левую часть этого выражения можно представить как
, (5.1)
так как в скобках значение сумма плотностей энергий электрического 
и равной ему плотности магнитного поля 
то в соответствии с (4.17) это выражение равно удвоенной плотности полной энергии 2 
, а для правой части воспользуемся формулой из векторного анализа
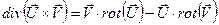, (5.2)
где 
и 
векторные функции, что в нашем случае
. (5.4)
Окончательно
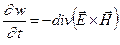. (5.5)
Если проинтегрировать это выражение по некоторому, произвольному объему и воспользоваться теоремой Гаусса
, (5.6)
где 
- произвольная векторная функция, 
- произвольный объем, 
- замкнутая поверхность, ограничивающая этот объем. Применяя к рассматриваемому случаю, получим
, (5.7)
где 
- полная энергия электромагнитного поля в объеме , а через 
(5.8)
обозначен вектор, называемый вектором Умова-Пойнтинга. Смысл выражения (5.7) заключается в том, что поток энергии через поверхность, окружающий некоторый объем, определяет уменьшение энергии в этом объеме. Этот поток описывается вектором и его размерность 
этому соответствует. Сравнивая (5.8) с (3.16) отметим, что коллинеарен вектору направления распространения волны 
, что выражает кажущуюся очевидность, однако это не так. В дальнейшем мы покажем, что в анизотропных средах направление потока энергии не совпадает с направлением распространения электромагнитной волны.
