6.1. Сыртқы электростатикалық өрістегі зарядтар жүйесі. Жұмыс және потенциалдық өріс.
6.2. Сыртқы электростатикалық өрістегі қатаң зарядтар жүйесіне әсер ететін күштер.
6.3. Зарядтардың әсерлесу энергиясы және электростатикалық өріс энергиясы.
6.1.Электростатикалық өрістің энергетикалық қатынасына тоқталайық. Өріске енген зарядтардың үстінен өріс тарапынан жасалатын жұмысты анықтайық.q зарядтардың үстінен электростатикалық өрістің атқаратын элементар жұмысын 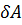 десек,
десек, 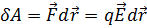 , Мұндағы:
, Мұндағы: 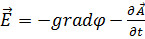 ,
, 
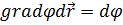 , Сонда
, Сонда 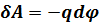 (6.1)
(6.1)  (6.1*)
(6.1*)
Электростатикалық өрістің q зарядты орынауыстырғанда өрістің атқаратын жұмысы.Бұл өрнектен электростатикалық өрістің q заряд үстінен атқаратын жұмысы зарядтардың бастапқы және соңғы нүктесіндегі потенциалының айырмасымен анықталады және заряд қозғалысының траекториясының түріне тәуелді болмайды.(6.1*) өрнекке сәйкес өрістің берілген нүктесіндегі потенциалдық энергиясы деген түсінік енгізіледі. 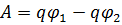
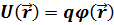 (6.2) - потенциалдық энергия.Сыртқы өрістегі зарядтар жүйесі үшін потенциалдық энергия былайша жазылады
(6.2) - потенциалдық энергия.Сыртқы өрістегі зарядтар жүйесі үшін потенциалдық энергия былайша жазылады
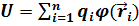 (6.3)
(6.3) 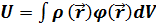
6.2. Кулон заңына сәйкес 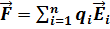 (6.4)
(6.4)
Нүктелік жүйенің жуықталған жағдайына сәйкес 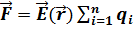 (6.5)
(6.5)
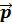 - дипольдік моментімен сипатталалатын электр жағынан бейтарап жүйеге әсер ететін күшті табу үшін
- дипольдік моментімен сипатталалатын электр жағынан бейтарап жүйеге әсер ететін күшті табу үшін  өрнегін пайдаланамыз.
өрнегін пайдаланамыз.
Потенциалдық өріс күштері үшін  шарты орындалатындықтан,
шарты орындалатындықтан, 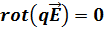 , Олай болса
, Олай болса 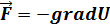
Бұдан біздің жағдай үшін, 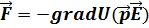 ,Есептеу кезінде II қосымшадағы 29 өрнекке сәйкес,
,Есептеу кезінде II қосымшадағы 29 өрнекке сәйкес,  Осығаан сәйкес және
Осығаан сәйкес және 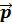 -ның
-ның  -ға тәуелді емес екенін ескерсек
-ға тәуелді емес екенін ескерсек 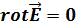 ,
,  ,
, 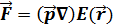 (6.6)
(6.6)
6.3 Зарядтардың әсерлесу энергиясы ж/е электростатикалық қріс энергиясы. Нүктелік зарядтар жүйесінің өзара әсерлесу энергиясын яғни жүйенің потенциалдық энергиясын қарастырайық. Жүйенің жекеленген зарядтарының әсерлесу энергиясы 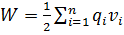 ;
;  (6.7)орнына қойсақ;
(6.7)орнына қойсақ; 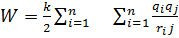 6.8 жүйедегі зарядтардың өзара әсерлесу энергиясы.
6.8 жүйедегі зарядтардың өзара әсерлесу энергиясы.
Егер заряд V көлемге үздіксіз таралған болса 6.8 өрнек келесідей интегралдық өрнекке алмастырылады. 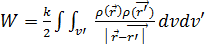 (6.9)
(6.9) 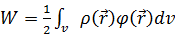 (6.9*)
(6.9*) 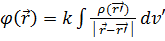 (6.10)Бұл өрнекті былайша қарастырайық.
(6.10)Бұл өрнекті былайша қарастырайық. 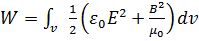 Өрнетен B=0 екенін ескерсек,
Өрнетен B=0 екенін ескерсек, 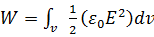 ;
; 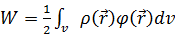 ;
;
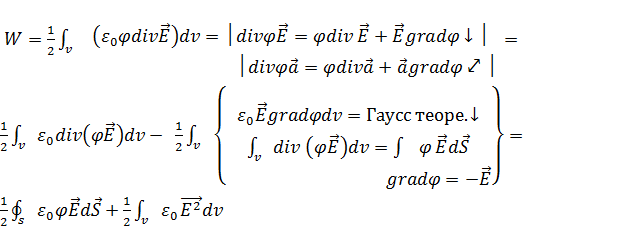 , сонымен,
, сонымен, 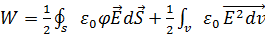 ,
, 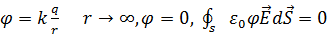 , сонымен, зарятдаржүйесінің потенциалды энергиясы, сол зарятдар жүйесі тудыратын өрістің энергиясына тең екендігі дәлелденді.
, сонымен, зарятдаржүйесінің потенциалды энергиясы, сол зарятдар жүйесі тудыратын өрістің энергиясына тең екендігі дәлелденді.
Лекция
Вакуммдегі магнитастатикалық өріс.
7. 1 Магнитостатикалық өріс теңдеудің потенциалдар арқылы жазылуы?
7.2 Вектор потенциал және магнитостатикалық өріс индукциясы?
7.1 Ток тығыздығы уақытқа байланысты өзгермей қалатын, яғни тұрақты жылдамдықпен қозғалатын зарядтың айналасында пайда болатын өріс магнитатикалық өріс деп аталады.
Магнитастатикалық өріс үшін Максвелл теңдеулері мына түрде жазылады:  =0 (7.1) Ал потенцал арқылы жазылуы:
=0 (7.1) Ал потенцал арқылы жазылуы:  (7.2) Мұндағы:
(7.2) Мұндағы: 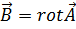 Бұл теңдеудің шешімі мына түрде жазылады:
Бұл теңдеудің шешімі мына түрде жазылады: 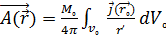 (7.3) (7.3)өрнектің жалпы шешімі Лаплас өрнегімен жазылады. Яғни
(7.3) (7.3)өрнектің жалпы шешімі Лаплас өрнегімен жазылады. Яғни 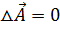 Сонымен қатар, магнитастатикалық өріс үшін Максвелл теңдеуінің интегралдық түрде жазылуы қолданылатын
Сонымен қатар, магнитастатикалық өріс үшін Максвелл теңдеуінің интегралдық түрде жазылуы қолданылатын 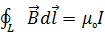 I-контурды қиып өтетін ток.
I-контурды қиып өтетін ток.
7.2
(7.3)-өрнекті пайдалана отырып құйынды магнитастатикалық өрістің индукциясын табайық ол үшін келесідей белгілеу енгізейік 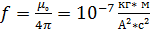 →индукциялық тұрақты.Осы индукциялық тұрақтының К тұрақтымен байланысы мына түрде жазылады:
→индукциялық тұрақты.Осы индукциялық тұрақтының К тұрақтымен байланысы мына түрде жазылады: 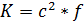 , К-кулон тұрақтысы.
, К-кулон тұрақтысы. 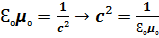 ,
, 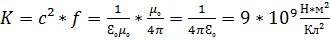
Осыны пайдаланып, 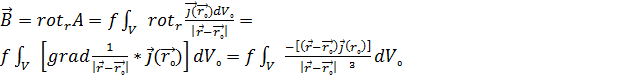
Сонда: 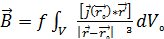
Бұл (7.4) өрнек Био-Савар Лаплас өрнегі болып табылады және магнитастатикалық өрістің кеңістіктің кез келген нүктесіндегі индукция векторын анықтауға мүмкіндік береді.






