Лоренц Максвелл теңдеулерін Классикалық механиканың заңдарымен байланысты қарастыруды ұсынды.Бірақ мұндай есепті шешу тиімсіз себебі нақты есепті жатпайды. Сондықтан Лоренц жоғардағы шешу үшін есепті берілуіне бірнеше екетпеулерді енгізу үсынды.
1.Тұйықталған жүйені әр дайым тандап алу мүмкін емес,себебі, өріске басқа өстер тарапынан әсерді шектеу мүмкін емес сондықтан сыртқы толқын көздері жоқ деп қарастыруды ұсынды, яғни қарастырылып жатқан жүйеге белгілі бір азғана шекті уақыт ішінде сырттан басқа өрістер әсер етпейді деп қарастырады.2.Зарядтар үнемі үдемелі қозғалыста болғанда “Реакциялық үйкеліс күші п.б.” Бұл күшті Ньютонның заңдары арқылы сипаттау мүмкін емес, сондықтан Лоренц бұл күшті ескермеуді ұсынды. 3.Зарядтар жұйесі үшін Классикалық механика заңдарын қолдану үшін Лоренц оларға механикалық модельдерді қолдануды ұсынды.Осы ұсыныстарды ескере келіп, Лоренц Максвелл теңдеулері былайша жазуды ұсынды.
1)  2)
2) 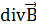 =0 3)
=0 3)  4)
4)  7;
7;
Лекция №3
Электромагниттік өрістің энергиясы және импульсі.
3.1. Зарядтың орын аыстыруы кезінде атқарылатын жұмыс.
3.2. Электромагниттік өрістің энергиясы. Энергияның сақталу заңы.
Эенргия және импульс әмбебап шамалар.Олар барлық физикалық нысандар үшін, оның ішінде Электромагниттік өріс үшін де негізгі шамалар болып табылады.Өзара әрекеттесетін зарядталған материалдық нүктелер жүйесін қарастырайық: Мұндай жүйе Максвелл- Лоренц теңдеулер жүйесімен сипатталады Осы теңдеулерді пайдалана отырып өріс- заряд тұйықталған жүйе үшін энергия және импульс түсініктерін қарастырайық.Макроскопиялық электр зарядтары материалдық денелермен байланысты, сондықтан массасы mі бөлшектің заряды qі деп қарастырайық. Мұндай дене үшін қозғалыс теңдеуі мына түрде жазылады:  (3.1)Теңдіктің екі жағынада элементар орын ауыстыру (qrі) көбейтейік; d
(3.1)Теңдіктің екі жағынада элементар орын ауыстыру (qrі) көбейтейік; d  d
d  (3.2) (3.2) теңдеуінің оң жағы Лоренц күшінің жұмысын береді.Лоренц күші 2 құраушыдан тұрады:1.Электрлік құраушы; 2.Магниттік құраушы;
(3.2) (3.2) теңдеуінің оң жағы Лоренц күшінің жұмысын береді.Лоренц күші 2 құраушыдан тұрады:1.Электрлік құраушы; 2.Магниттік құраушы;  =q
=q  +q
+q  (*)Бірақ Лоренц күщінің магниттік құраушысы жұмыс жасамайды.Себебі,Лоренц күші орын ауыстыруға әрқашанда перпендикуляр.яғни:
(*)Бірақ Лоренц күщінің магниттік құраушысы жұмыс жасамайды.Себебі,Лоренц күші орын ауыстыруға әрқашанда перпендикуляр.яғни: 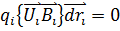 (3.3) Лоренц күшінің элементар жұмысы зарядталған материалдық нүктенің реаливистік энергиясының өсімшесіне тең болады. Элементар жұмыстарды біріктерсек
(3.3) Лоренц күшінің элементар жұмысы зарядталған материалдық нүктенің реаливистік энергиясының өсімшесіне тең болады. Элементар жұмыстарды біріктерсек  (3.4) өрнек материалдық нүктелер жүйесі үшін энергияның өзгеру теоремасы деп аталады.Бірлік уақыт ішіндегі өрістің жұмысын табу үшін(3.4)өрнектің оң жағын интегралдаймыз:
(3.4) өрнек материалдық нүктелер жүйесі үшін энергияның өзгеру теоремасы деп аталады.Бірлік уақыт ішіндегі өрістің жұмысын табу үшін(3.4)өрнектің оң жағын интегралдаймыз:  (3.5)өрнектен қуаттың тығыздығын,яғни бірлік көлемде бірлік уақыттағы атқарылатын жұмысты табуға болады.
(3.5)өрнектен қуаттың тығыздығын,яғни бірлік көлемде бірлік уақыттағы атқарылатын жұмысты табуға болады.  (3.6)
(3.6)
3.2  векторлары берілген болсын, солардың көмегімен электромагниттік өрістің энергиясын анықтайық.Электродинамикадағы себептілік принципіне сәйкес бастапқы уақыт мезетіндегі электромагниттік өрісті сипаттайтын
векторлары берілген болсын, солардың көмегімен электромагниттік өрістің энергиясын анықтайық.Электродинамикадағы себептілік принципіне сәйкес бастапқы уақыт мезетіндегі электромагниттік өрісті сипаттайтын  және
және  алдағы кез-келген уақыт мезетіндегі кеңістіктің кез-келген нүктесіндегі өрістің сипаттамаларын дәл анықтауға болады.Максвелл теңдеулерінен:
алдағы кез-келген уақыт мезетіндегі кеңістіктің кез-келген нүктесіндегі өрістің сипаттамаларын дәл анықтауға болады.Максвелл теңдеулерінен:
 =
= 
 +
+ 
rot  =-
=- 
rot 
3.3 Өріс-заряд тұйықталған жүйесін қарастырайық;
Алдымен (3.10)-шы өрнектен энергияның сақталу заңының тұжырымдарын келтірейік:Белгілі бір көлемдегі энергияның кемуі сол көлемнен шығып жатқан энергия ағыны мен осы жүйедегі зарядтар үстінен өрістің атқаратын жұмысына тең болады.Тұйықталған жүйеде сәулелену интенсивтілігі (ағыны) ескерілмейтіндіктен (3.9)-шы өрнектен
 +
+  )dV=
)dV= 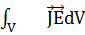 (3.11)
(3.11)
(3.11)-ші өрнектен тұйықталған жүйедегі зарядтар үстінен өрістің жасайтын жұмысы сол өрістің энергиясының кемуі есебінен атқарылады. Тұйықталған өріс-заряд жүйесі үшін энергияның сақталу заңын қорытып алайық. Ол үшін (3.11)-ші оң жағы жұмыс екендігін ескерсек (3.4)-ші өрнекке сәйкес
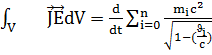 Cонда
Cонда
-  )dV=
)dV=  ;
;
 )=0 (3.12)
)=0 (3.12)
Тек тұрақты шаманың туындысы 0-ге тең болатындықтан (3.12)-ші теңдеудің жақша ішіндегі шаманы  (
( (3.13)-шы өрнек өріс-заряд тұйықталған жүйесі үшін энергияның сақталу заңы деп аталады.
(3.13)-шы өрнек өріс-заряд тұйықталған жүйесі үшін энергияның сақталу заңы деп аталады.
3.4 Электромагниттік өрістің импульсінің теңдеуі келесідей жолмен алынады. Электромагниттік өріс үшін қозғалыс теңдеуі
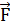 =m
=m  =
= 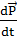
 =
= 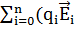 +
+  [
[  ])
])
Зарядтың кеңістікте таралуын үздіксіз болса онда (3.14)-ші теідіктің оң жағындағы қосындыны интегралмен алмастыруға болады.
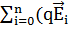 +
+  [
[  ]=
]=  (ρ
(ρ  +[
+[  ]dV.
]dV.
q=ρdV;  =
=  ;
;
 =
=  (ρ
(ρ  +[
+[  ])dV (3.15)-ші өрнектің оң жағындағы жақша ішіндегі өрнекті түрлендірейік
])dV (3.15)-ші өрнектің оң жағындағы жақша ішіндегі өрнекті түрлендірейік
ρ  +[
+[  ]=
]=  div
div  -
-  [
[  ]+
]+
 [rot
[rot  ]. (3.16)
]. (3.16)
ρ=  div
div  ;
;
rot  =
= 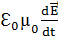 +
+  =>
=>  =
=  rot
rot  -
- 
(3.16)-шы өрнектің оң жағын уақыттың толық туындысы болатын қандайда бір шамаға келтіру үшін оған мынандай қосымша қояйық
-  [
[  ]-
]-  [
[ 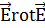 ]
]
ρ  +[
+[  ]=
]=  -
- 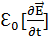 +
+  [rot
[rot  ]-
]-  -
-  (3.1
(3.1 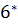 )
)
Бұл теңдеудің оң жағын біріктірейік (топтастырайық);
 +
+  =-
=-  +
+  (
( -
-  +
+  (
( +
+  )
)
(3.1  )-шы өрнекті ескеріп (3.15) – ші теңдеуді мына түрде жазуға болады.
)-шы өрнекті ескеріп (3.15) – ші теңдеуді мына түрде жазуға болады.
 =-
=-  dV (3.1
dV (3.1  )
)
Төртінші қосымшаға (векторлық анализдің)өрнектеріне сәйкес
 (
( div
div  -
-  dV=0
dV=0
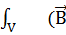 div
div  -
-  =0 екендігін ескерсек
=0 екендігін ескерсек
 =-
=-  dV (3.1
dV (3.1  )
)
 (3.17)
(3.17)
Тек тұрақты шаманың туындысы 0-ге тең болатындықтан
 +
+  (3.1
(3.1  )
)
(3.1  )-ші өрнек өріс-заряд тұйықталған жүйесі үшін импульстің сақталу заңы деп аталады.
)-ші өрнек өріс-заряд тұйықталған жүйесі үшін импульстің сақталу заңы деп аталады.  =
=  – импульс тығыздығы деп аталады.
– импульс тығыздығы деп аталады.
Лекция №4
\ Электромагниттік өрістің потенциялдары үшін теңдеулері






