С помощью колец Ньютона
Приборы ипринадлежности: стеклянная линза, смонтированная с плоской пластинкой; микроскоп; масштабная линейка с известной ценой деления; светофильтр, пропускающий свет известной длины волны; светофильтр, пропускающий свет неизвестной длины волны.
Цель работы: определить радиус кривизны линзы и длину волны лазерного излучения с помощью колец Ньютона.
Теоретическое введение
Классическим примером полос равной толщины являются кольца Ньютона. Если осветить монохроматическим светом плосковыпуклую линзу с большим радиусом малой кривизны, положенную сферической поверхностью на плоскую стеклянную пластину, то при наблюдении отраженного света будут видны кольца Ньютона (чередующиеся темные и светлые кольца с темным пятном в центре, рис. 1.6, 1.7). Кольца Ньютона являются результатом интерференции световых волн, одна из которых отражается от поверхности АОВ, другая - от поверхности DOC.
 |  | ||
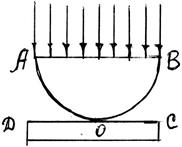Толщина воздушного слоя между этими поверхностями постепенно увеличивается по всем направлениям от точки их соприкосновения, и полученные полосы равной толщины будут представлять собой концентрические окружности с центром в точке O.
|
При отражении света от поверхности DОC (оптически более плотной среды) происходит потеря полуволны, поэтому оптическая разность хода между интерферирующими лучами
D = 2 b + l/2, (1.21)
где b - толщина зазора между сферической DОВ иплоской DОС поверхностями.
С учетом формул (1.21), (1.8), (1.9) получим следующие условия:
2 b = (2 k -1) l/2 – (1.22)
максимум интенсивности отраженного света;
2 b = 2 k l/2 – (1.23)
минимум интенсивности отраженного света,
где k - целое число.
Следовательно, в тех местах, где удвоенная толщина воздушного зазора равна нечетному числу полуволн, в отраженном свете будут наблюдаться светлые кольца, а там, где удвоенная толщина воздушного зазора равна четному числу полуволн, - темные кольца.
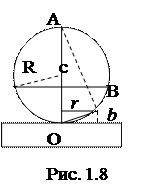
Установим зависимость между радиусами наблюдаемых колец Ньютона r, толщиной воздушного слоя b и радиусом поверхности линзы R. На рис. 1.8 DАOВ прямоугольный, его высота r есть среднегеометрическое между отрезками диаметра
2 R - b и b, т.е.
, (1.24)
отсюда
r 2 = b (2 R – b). (1.25)
Учитывая, что R >> b, получим
R = r 2 / 2 b. (1.26)
Поскольку для темного кольца 
(см. условие (1.23)),
R = r 2 k / k l. (1.27)
Зная радиус кривизны поверхности линзы, можно определить длину волны света, падающего на интерференционную систему. На основании условий (1.23) и (1.26) для k -гo и (k + m)-го колец можно записать
и (1.28)
.
Из этих равенств имеем
, (1.29)
где rk, rm+k – радиусы k -гo и (k + m)-го темных колец.
Описание установки и порядок выполнения работы
Схема установки изображена на рис 1.9, где 1 - осветитель;
2 - светофильтр; 3 - окуляр микроскопа; 4 - объектив микроскопа;
5 - переключатель увеличения микроскопа; 6 - рукоятка фокусировки;
7 - предметный столик; 8 - линза, смонтированная с пластиной.
Свет от лампы накаливания осветителя 1 проходит через светофильтр 2, падает вертикально на линзу, смонтированную с плоскопараллельной пластиной 8, и после отражения наблюдается через окуляр 3.
Задание 1. Измерение радиуса колец Ньютона в делениях окулярной шкалы
1. Включить осветитель микроскопа 1.
2. Установить светофильтр 2 (l= 546 нм).
3. Положить на столик микроскопа линзу.
4. Передвигая линзу, изменяя ручкой 5 увеличение микроскопа и фокусируя картину колец ручкой 6, получить резкое изображение колец Ньютона. Окулярная шкала при этом должна располагаться по диаметру колец.
5. 
Измерить координаты (по окулярной шкале) середин пересечения нескольких темных колец с окулярной шкалой, например, третьего и шестого колец (рис. 1.10).
6. Вычислить радиусы колец в делениях шкалы, например, для третьего кольца
.
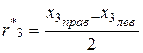7. Повторить указанные в пп.5 и 6 измерения и вычисления два раза. Определить среднее значение радиусов колец.
Задание 2. Определение цены деления окулярной шкалы
1. Поместить на столик микроскопа вместо линзы с пластинкой масштабную линейку, цена деления которой a0 известна.
2. Добившись фокусировки при том же увеличении микроскопа, что и в задании 1, сравнить окулярную шкалу с масштабной и определить цену деления а окулярной шкалы. Для этого заметить, какое число m целых делений масштабной линейки имеют такую же длину, как и n целых делений окулярной шкалы. Затем из равенства mа 0 = na вычислить
a = a0 m / n.
3. Повторить указанные в п. 2 измерения два раза и определить среднее значение величины α.
Задание 3. Вычисление радиуса кривизны линзы и длины волны света
1. По формуле (1.27) вычислить значение радиуса кривизны линзы, используя данные о двух разных кольцах k -гo и (k + m)-гo порядков и учитывая, что rk = r*k a:
; 
.
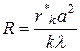2. Найти среднее значение радиуса кривизны линзы.
3. Сменить светофильтр. Измерить радиусы k -го и (k + m)-гo колец Ньютона.
Используя полученное значение радиуса кривизны линзы по формуле (1.29), вычислить длину волны света, прошедшего через светофильтр.
Контрольные вопросы
Вариант 1
1. Какой свет называется монохроматическим, а какой когерентным?
2. Какое будет в центре пятно (светлое или темное) при наблюдении колец Ньютона в проходящем свете?
3. Выведите рабочую формулу для определения длины световой волны с помощью колец Ньютона.
4. Задача. Фронт волны желтого света прошел в стекле за некоторое время путь, равный 10 мм. Какой путь пройдет он за то же время в воде?
(nст = 1,50. nв =1,33).
Ответ: l = 11,3 м.
Вариант 2
1. Перечислите методы получения когерентных волн.
2. Выведите рабочую формулу для расчета радиуса кривизны линзы.
3. В чем состоит "просветление" оптики?
4. Задача. Длина волны желтого света в воздухе равна 5890 Å. Какова длина волны этого света в воде (nв = 1,33) и в стекле (nст = 1,50)?
Ответ: l1 = 143 нм; l2 = 393 нм.
Вариант 3
1. Объясните природу радужной окраски некоторых поверхностей (мыльного пузыря, металла, крылышек насекомых).
2. Нарисуйте схему опытов для наблюдения полос равной толщины.
3. Выведите условия интерференционных максимумов и минимумов.
4. Задача. Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластике. Определить толщину слоя воздуха в том месте, где в отраженном свете (l = 0,6 мкм) видно первое светлое кольцо Ньютона.
Ответ: b = 0,15 мкм.
Лабораторная работа № 3-03
Определение длины волны лазерного излучения методом интерференции света, прошедшего через бипризму Френеля
Приборы и принадлежности: оптическая скамья,снабженная линейкой; лазер ЛГ-72; источник питания лазера ИП-10, щелевая диафрагма; бипризма Френеля с преломляющим углом a; cобирающая линза; непрозрачный белый экран с горизонтальной и вертикальной шкалами с миллиметровыми делениями.
Цель работы: ознакомиться с явлением интерференции световых волн, прошедших через бипризму Френеля, измерить длину волны лазерного излучения интерференционным методом.
Теоретическое введение
Бипризма Френеля представляет собой две призмы с малыми преломляющими углами a, сложенные основаниями (рис. 1.11).
Свет от щели S после преломления в бипризме делится на два перекрывающихся пучка, исходящих от двух мнимых изображений щели S1 и S2, являющихся когерентными источниками. При этом за призмой в области пересечения пучков наблюдается интерференционная картина в виде чередующихся светлых и темных полос, параллельных щели S. Расстояние между соседними светлыми полосами на экране согласно соотношению (1.11) равно
D y = L l 0 / d, где L - расстояние от плоскости, в которой лежат мнимые источники S1 и S2, до экрана; d - расстояние между мнимыми источниками.
Отсюда
l 0 = D y d / L. (1.31)
Расстояние между мнимыми источниками d можно определить, зная показатель преломления стекла бипризмы n, ее преломляющий угол a и измерив расстояние a между щелью S и призмой. Так как преломляющие углы бипризмы малы, то с достаточной точностью можно считать, что S1, S2 и S лежат в одной плоскости, перпендикулярной оптической оси (рис. 1.12).
Из рис. 1.12 видно, что
d = 2 a tg j» 2 a j, (1.32)
так как угол j мал. Угол отклонения j связан с преломляющим углом a по формуле j = (n – 1) a, где n – показатель преломления стекла бипризмы.
Отсюда
d = 2 a (n –1) a. (1.33)
Следовательно,
l 0 = 2 a (n –1) a D y / L. (1.34)
Короткофокусная линза 4 служит для получения увеличенного изображения на экране 5 интерференционных полос, возникающих в области между бипризмой 3 и линзой 4.
Из этого рисунка видно, что ширина интерференционной поло-сы D y в формуле (1.34) выражается через ширину полосы на экране D y ¢ следующим образом:
. (1.35)
Неизвестное расстояние b ¢ можно найти с помощью формулы для тонкой линзы:
, (1.36)
откуда
. (1.37)
Следовательно,
. (1.38)
Из рис. 1.13 следует, что
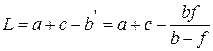.(1.39)
Подставляя выражения (1.38) и (1.39) в формулу (1.34), окончательно получим:
. (1.40)
Описание установки и порядок выполнения работы
Схема установки изображена нарис. 1.14, где
1 - лазер; 2 - щелевая диафрагма; 3 - бипризма Френеля; 4 - собирающая линза; 5 - экран.
В качестве источника световых волн используется лазер ЛГ-72, излучающий узкий пучок (диаметром 1,5 мм) монохроматического света. Мощность лазера 0,5 мВт.
1. Установить приборы на оптической скамье согласно
рис. 1.14. На расстоянии 5...10 см от лазера 1 поместить щелевую диафрагму 2, зa ней на расстоянии З0...40 см - бипризму Френеля 3, далее на расстоянии 50...70 см - линзу 4 и, наконец, на расстоянии 20...30 см от линзы - экран 5. Центры всех размещенных приборов должны находиться на одной высоте. Окончательную центровку приборов осуществляют при включенном лазере.
2. Включить лазер. Для этого: 1) вставить вилку от источника питания лазера ИП-10 в сетевую розетку 220 В; 2) включить тумблер "Сеть" на панели источника ИП-10, при этом должна загореться лампочка "Сеть". Через несколько минут лазер готов к работе.
3. Отъюстировать установку, добиваясь, чтобы луч лазера попадал на щель 2 и общую грань призм бипризмы 3, а светящаяся полоска с интерференционными полосами в пучке лучей за бипризмой попала в центр короткофокусной линзы 4.
Слегка перемещая вдоль оптической оси бипризму 3 и линзу 4, добиться, чтобы на горизонтальной шкале экрана 5 наблюдалась отчетливая картина вертикально расположенных интерференционных полос. При юстировке следует помнить, что прямой лазерный луч не должен попадать в глаз.
4. Измерить ширину интерференционной полосы D y ¢. Для этого с помощью шкалы на экране 5 измерить расстояние q между серединами крайних m = 5... 10 светлых (темных) полос. Ширина полосы D y ¢ = q / (m - 1). Этот опыт повторить три раза и найти среднее значение.
5. По линейке, закрепленной на оптической оси, измерить расстояния b, с, a.
6. Используя полученные значения D y ¢, b, с, a, по формуле (1.40) рассчитать l 0 (n = 1,457; a = 22¢; f = 35,83 мм), минуты перевести в радианы.
7. Изменить положение бипризмы и линзы, добиться новой четкой интерференционной картины. Повторить пп. 4 - 6 и еще раз рассчитать l0.
8. Найти среднее значение длины волны лазерного излучения l0 по двум независимым измерениям.
Контрольные вопросы
Вариант 1
1. В чем заключается явление интерференции света?
2. Напишите условия интерференционных максимумов и минимумов.
3. Нарисуйте ход лучей в бипризме Френеля.
4. Задача. Найти все длины волн видимого света (от 0,76 до 0,38 мкм), которые будут максимально усилены и максимально ослаблены при разности хода интерферирующих лучей D = 1,8 мкм.
Ответ: l1 = 0,6, l2 = 0,45 мкм.
Вариант 2
1. Почему не наблюдается интерференция от двух независимых источников света?
2. Нарисуйте схему установки для определения длины волны с помощью бипризмы Френеля.
3. Выведите расчетную формулу для определения длины волны с помощью бипризмы Френеля.
4. Задача. Расстояние между светлыми полосами наэкране в средней части интерференционной картины равно 1см. Расстояние между двумя когерентными источниками света (l = 0,5 мкм) равно 0,1 мм. Определить расстояние от источника до экрана.
Ответ: 2 м.
Вариант 3
1. Что такое когерентные лучи? Перечислите методы получения когерентных световых пучков.
2. Как определяется расстояние между двумя мнимыми источниками в бипризме Френеля?
3. Выведите формулу, определяющую положение интерференционного максимума на экране.
4. Задача. В опыте Юнга расстояние d между щелями равно 0,8 мм. На каком расстоянии l от щелей следует расположить экран, чтобы ширина интерференционной полосы оказалась равной 2 мм (l = 6328 Å)?
Ответ: l = 2,5 м.
Лабораторная работа № 3-04
