Интерференция света
Интерференция волн – явление усиления или ослабления амплитуды результирующей волны в зависимости от соотношения между фазами накладывающихся в пространстве двух (или нескольких) волн с одинаковыми периодами. Интерференция имеет место для всяких волн независимо от их природы (упругих, электромагнитных и др.). Она может наблюдаться только при выполнении условия когерентности накладывающихся волн. Волны являются когерентными, если они имеют одинаковую частоту и разность фаз между ними в какой-либо точке пространства не меняется во времени.
Когда в пространстве распространяются две волны, то в случае, если среда, в которой они распространяются, линейна (т.е. отсутствует зависимость свойств среды от интенсивности волны), соблюдается принцип суперпозиции и результирующее колебание представляет собой сумму колебаний, соответствующих каждой из накладывающихся волн.
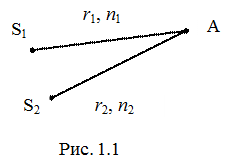 Рассмотрим простейший пример наложения двух когерентных световых волн, распространяющихся от источников S1 и S2. Предположим, что пространство между источником S1 и точкой А заполнено средой с показателем преломления n 1, а пространство между источником S2 и точкой А - средой с показателем преломления n 2 (соответствующие геометрические расстояния между точкой А и источниками S1 и S2 равны r 1 и r 2, рис. 1.1). Уравнения накладывающихся бегущих волн в точке А имеют вид
Рассмотрим простейший пример наложения двух когерентных световых волн, распространяющихся от источников S1 и S2. Предположим, что пространство между источником S1 и точкой А заполнено средой с показателем преломления n 1, а пространство между источником S2 и точкой А - средой с показателем преломления n 2 (соответствующие геометрические расстояния между точкой А и источниками S1 и S2 равны r 1 и r 2, рис. 1.1). Уравнения накладывающихся бегущих волн в точке А имеют вид
E 1 = E 10 cos ω (t – τ 1); E 2 = E 20 cos ω (t – τ 2), (1.1)
где E10 и Е20 –амплитуды накладывающихся колебаний; τ1 и τ2 – время распространения колебаний от источников S1 и S2 до точки наблюдения А.
Если υ 1 и υ 2 – скорости распространения волн в первой и во второй среде, то
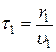 ;
; 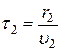 .
.
С учетом этого формулы (1.1) приобретут вид:
 (1.2)
(1.2)
 Амплитуду результирующего колебания найдем графическим методом. На рис. 1.2 изображена векторная диаграмма сложения двух колебаний с амплитудами Е 10 и Е 20.
Амплитуду результирующего колебания найдем графическим методом. На рис. 1.2 изображена векторная диаграмма сложения двух колебаний с амплитудами Е 10 и Е 20.
Амплитуда результирующего колебания
Е 0 = 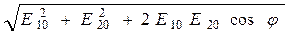 , (1.3)
, (1.3)
где 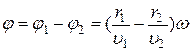 .
.
Поскольку плотность потока энергии волны j пропорциональна квадрату ее амплитуды, то результирующая плотность потока энергии (интенсивность)
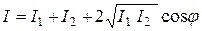 . (1.4)
. (1.4)
Разность фаз взаимодействующих волн может быть выражена через длину волны излучения в вакууме λ0, геометрические (r1 и r2) и оптические (n1 и n2) параметры сред. Учитывая, что
 ;
; 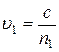 ;
;  , (1.5)
, (1.5)
имеем
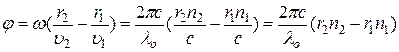 . (1.6)
. (1.6)
Величины n 1 r 1 и n 2 r 2 называются оптическими длинами путей, а их разность
Δ = n 1 r 1 – n 2 r 2 – (1.7)
оптической разностью хода.
Из соотношения (1.4) видно, что при наложении волн, создаваемых когерентными источниками света, результирующая интенсивность не равна сумме интенсивностей, создаваемых отдельными источниками. Максимальная интенсивность наблюдается в точках, для которых выполняется условие соs φ = 1, минимальная - при соs φ = -1.Таким образом, условие усиления волны имеет вид
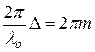 , или
, или  , (1.8)
, (1.8)
условие ослабления —
 , или
, или  , (1.9)
, (1.9)
где m — целое число.
Соотношения (1.8) и (1.9) показывают, что максимальной освещенности соответствует оптическая разность хода лучей, равная четному числу полуволн, а минимальной - разность хода лучей, равная нечетному числу полуволн. Величина k определяет порядок максимума иминимума и принимает значения 0, ±1, ±2,....В результате интерференции на экране возникает совокупность светлых итемных полос. При интерференции усиление освещенности в одних местах происходит за счет ее ослабления, в других - согласно закону сохранения энергии.
При оптической разности хода  , cos φ = 1 и в соответствии с формулой (1.4)
, cos φ = 1 и в соответствии с формулой (1.4)
I = I1 + I2 + 2  ,
,
а при оптической разности хода
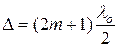 ;
;
 .
.
Если интенсивности накладывающихся волн равны (I 1 = I 2 = I 0), максимуму интенсивности соответствует I = 4 I 0, а минимуму – I =0.
В этом случае интерференционная картина будет наиболее четкая.
Естественные источники света не являются когерентными. Это обусловлено тем, что излучение светящегося тела слагается из волн, испускаемых многими атомами. Отдельные атомы излучаютцуги волн длительностью 10-8 с. Фаза нового цуга волн никак не связана с фазой предыдущего цуга, а также с фазами цугов волн других атомов. В испускаемой телом световой волне излучение одной группы атомов сменяется излучением другой группы атомов, аразность фаз между слагающимися волнами является случайной величиной. При этом происходит простое суммирование интенсивностей взаимодействующих волн, не приводящее к перераспределению энергии в пространстве.
Если условие когерентности волн выполняется, то в пространстве получается некоторое неизменное распределение амплитуд результирующей волны с чередующимися максимумами и минимумами.
Когерентные световые волны можно получить путем деления волны, испускаемой каким-либо источником света, на две волны, разность фаз между которыми зависит от оптической разности хода и не изменяется во времени. При этом разность хода не должна быть большой, так как интерферирующие волны должны принадлежать одному и тому же цугу волн. Если это условие нарушается, то разность фаз между ними будет изменяться с течением времени.
Интерференцию света можно наблюдать, используя зеркала Френеля, или бипризму Френеля, или щели Юнга.
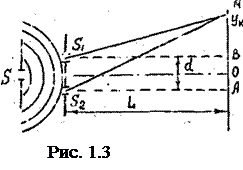 В методе Юнга источником света служит щель S, от которой цилиндрическая световая волна падает на две узкие параллельные щели S1 и S2 (рис. 1.3). Таким образом, щели освещаются различными участками одной и той же волновой поверхности и на основании принципа Гюйгенса –Френеля они являются источниками вторичных когерентных волн. Рассмотрим волны, которые распространяются вдоль направлений S 1 M и S2 М и взаимодействуют на экране, удаленном от плоскости щелей на расстояние L» d (d - расстояние между щелями). Оптическая разность хода этих волн
В методе Юнга источником света служит щель S, от которой цилиндрическая световая волна падает на две узкие параллельные щели S1 и S2 (рис. 1.3). Таким образом, щели освещаются различными участками одной и той же волновой поверхности и на основании принципа Гюйгенса –Френеля они являются источниками вторичных когерентных волн. Рассмотрим волны, которые распространяются вдоль направлений S 1 M и S2 М и взаимодействуют на экране, удаленном от плоскости щелей на расстояние L» d (d - расстояние между щелями). Оптическая разность хода этих волн
Δ = S 2 M - S 1 М (n 1= n 2 = 1).
Из треугольников S 1 MВ и S 1 MА следует, что
S 1 M 2 = L 2 +(ym – d /2)2;
S 2 M 2 = L 2 +(ym + d /2)2,
откуда (S 1 M + S 2 M)(S 2 M - S 1 M) = 2 ymd.
Поскольку L >> d, S 1 M + S 2 M ≈ 2L,
то 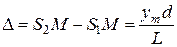 .
.
Максимальная освещенность наблюдается при выполнении условия (1.8). Этому условию соответствуют значения ym,удовлетворяющие соотношению
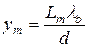 . (1.10)
. (1.10)
Расстояние между соседними максимумами (минимумами)
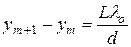 . (1.11)
. (1.11)
Оно тем больше, чем сильнее неравенство L >> d.
Если щели S1 и S2 освещены белым светом, то интерференционная картина имеет следующий вид. В центре картины расположен максимум нулевого порядка, окрашенный в белый цвет. По обе стороны от него находятся спектры первого и высших порядков (m ³ 1). В спектре каждого порядка ближайший к центру край окрашен в фиолетовый цвет, удаленный - в красный. В спектрах высших порядков (m > 3) наблюдается наложение максимумов разных длин волн и разных порядков, поэтому интерференционная картина размывается.
Лабораторная работа № 3-01
Определение показателя преломления стекла интерференционным методом
Приборы и принадлежности: лазер ЛГ-72 с источником питания ИП-13; стеклянная плоскопараллельная пластина; матовый экран с короткофокусной линзой.
Цель работы: определить показатель преломления стекла, используя явление интерференции света в стеклянной плоскопараллельной пластинке.
Теоретическое введение
Рассмотрим интерференцию света в тонких плоскопараллельных пластинках (рис. 1.4).
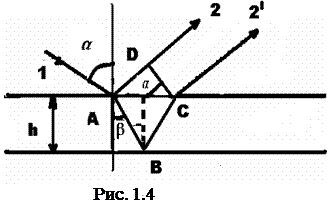 На пластинку толщиной h падает параллельный монохроматический пучок света (1) с длиной волны
На пластинку толщиной h падает параллельный монохроматический пучок света (1) с длиной волны 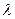 . Пластинка отбрасывает вверх два параллельных пучка света, один из которых (пучок 2) образуется за счет отражения от верхней поверхности пластинки, другой (пучок 2¢) – вследствие отражения от нижней поверхности (на рисунке каждый из этих пучков представлен только одним лучом). При входе в пластинку и при выходе из нее пучок 2¢ претерпевает преломление. Лучи 2 и 2¢ когерентны, т.к. они идут от одного источника света и будут обладать некоторой разностью хода.
. Пластинка отбрасывает вверх два параллельных пучка света, один из которых (пучок 2) образуется за счет отражения от верхней поверхности пластинки, другой (пучок 2¢) – вследствие отражения от нижней поверхности (на рисунке каждый из этих пучков представлен только одним лучом). При входе в пластинку и при выходе из нее пучок 2¢ претерпевает преломление. Лучи 2 и 2¢ когерентны, т.к. они идут от одного источника света и будут обладать некоторой разностью хода.
Определим оптическую разность хода лучей 2 и 2¢. Для этого опустим перпендикуляр из точки С на луч 2 и получим фронт плоской падающей волны ДС. Тогда разность хода лучей
Δ = (AB + BC) n – (АD – λ /2).
Длина пути второго луча уменьшена на λ /2, так как он отражается от оптически более плотной среды и при этом происходит потеря полуволны. Из рис. 1.4 видно, что АВ = ВС= h /cos β. Принимая во внимание закон преломления света sin α = n sin β, получим
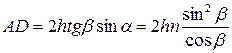 .
.
Тогда
 . (1.12)
. (1.12)
Выражая Δ через угол падения, найдем
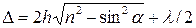 . (1.13)
. (1.13)
Если разность хода лучей Δ равна четному числу полуволн, то световые лучи при наложении будут усиливать друг друга. Если же Δ равна нечетному числу полуволн, то эти лучи будут взаимно ослабляться. Поэтому условие максимального усиления света, отраженного от плоскопараллельной пластинки, имеет вид
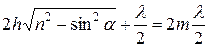 либо
либо 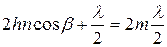 ,
,
или
 либо
либо  , (1.14)
, (1.14)
где m – целое число, (m = ±1, ±2…), а условие минимума отраженного света -
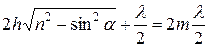 либо
либо 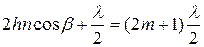 ,
,
или
 либо
либо 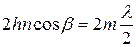 , (1.15)
, (1.15)
где m - целое число (m = 0, ±I, ±2...).
Если поверхности пластинки строго параллельны, то в зависимости от угла падения монохроматического света пластина будет видна либо освещенной, либо темной.
Если на пластинку падает расходящийся пучок лучей, соответствующий, например, сферической волне, то падающие лучи будут составлять с поверхностью пластинки разные по величине углы. Каждому падающему лучу будет соответствовать пара лучей, отраженных от верхней и нижней поверхностей пластинки. Оптические разности хода между лучами каждой пары выражаются формулой (1.13). Они неодинаковы для различных участков пластины, так как углы падения света на эти участки различны.
Для наблюдения интерференции в отраженном свете используются собирательная линза 2 и экран 3, расположенный в фокальной плоскости линзы (рис 1.5). При освещении плоскопараллельной пластинки монохроматическим светом результат интерференции отраженного света в различных точках экрана зависит только от угла падения света на пластину. Интерференционная картина имеет вид чередующихся темных и светлых полос. Каждой из этих полос соответствует определенное значение угла падения a, поэтому образующиеся линии называются линиями равного наклона.
В случае, если оптическая ось линзы перпендикулярна поверхности пластинки, полосы равного наклона имеют вид концентрических колец с центром в главном фокусе линзы.
Это явление используется для определения показателя преломления стекла.
Вывод рабочей формулы
Интерференционное условие m -минимума в отраженном свете согласно формуле (1.15) имеет вид
2 hncos bm = ml,
где h - толщина пластинки; n - показатель преломления стеклянной пластинки; b - угол преломления m -го луча света в пластинке; m - порядок интерференции; l - длина волны света.
Для другого минимума, отстоящего от m -го на k полос, запишем аналогично:
2 hncos bm+k = (m + k) l.
Взяв разность этих выражений, получим
kl = 2 h n (cos bm+k – cos bm). (1.16)
Для малых углов bm+k и bm, разлагая функции cosbk+m и cosbk
в ряд и ограничиваясь первым приближением cos b» 1 – b 2/2, имеем
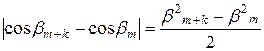 . (1.17)
. (1.17)
Угол преломления связан с углом падения для малых углов следующим образом:
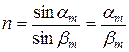 . (1.18)
. (1.18)
Из D ОВС, изображенного на рис. 1.5, следует, что
am = Rm /2 L, (1.19)
где Rm - радиус темного кольца m -гo порядка; L - расстояние от стеклянной пластины до экрана.
Подставив формулы (1.17) - (1.19) в соотношение (1.16), получим
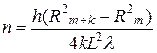 . (1.20)
. (1.20)
Измерив радиусы двух темных дифракционных колец, толщину пластины и расстояние между пластинкой и экраном, по формуле (1.20) рассчитаем показатель преломления стекла.
Порядок выполнения работы
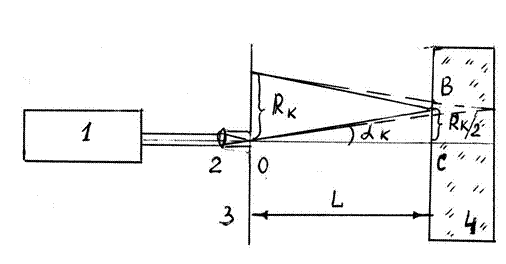
На рис. 1.5 изображена оптическая схема установки, где
1 - лазер; 2 - короткофокусная линза; 3 - экран; 4 - плоскопараллельная пластинка.
 |
Большая пространственная и временная когерентность лазерного излучения позволяет применять лазерный световой пучок мощностью в несколько милливатт для наблюдения интерференционных полос равного наклона в достаточно толстой плоскопараллельной пластинке.
Для определения показателя преломлениястекла интерференционным методом необходимо:
1) включить источник питания ИП-13 в сеть, включить лазер;
2) установить экран с линзой вблизи лазера так, чтобы луч попадал в отверстие экрана;
3) установить стеклянную пластинку так, чтобы на экране были четко видны светлые и темные кольца;
4) по шкале на экране измерить радиусы двух темных колец Rk и Rk+rn, желательно, чтобы число m было большим;
5) с помощью шкалы на оптической скамье измерить расстояние от экрана до передней поверхности стеклянной пластинки;
6) зная длину волны лазера (l= 6328 Å), толщину стеклянной пластинки (h = 17 мм) и используя результаты измерений, с помощью соотношения (1.20) вычислить показатель преломления стекла, из которого изготовлена плоскопараллельная пластина.
Контрольные вопросы
Вариант 1
1. В чем заключается явление интерференции?
2. Выведите формулу для оптической разности хода лучей при отражении от плоскопараллельной пластинки.
3. Что такое полосы равного наклона?
4. Перечислите основные свойства излучения оптического квантового генератора.
5. Задача. На мыльную пленку падает белый свет под углом a = 45° к поверхности пленки. При какой наименьшей толщине пленки отраженные лучи будут окрашены в желтый цвет (l= 600 нм)? Показатель преломления мыльной воды n = 1,33.
Ответ: h = 0,13 мкм.
Вариант 2
1. Что называется оптической разностью хода лучей?
2. Выведите рабочую формулу для определения показателя преломления стекла.
3. Нарисуйте схему установки для получения полос равного наклона.
4. Приведите примеры практического применения явления интерференции в технике.
5. Задача. На пути монохроматического света с длиной волны l = 0,6 мкм находится плоскопараллельная стеклянная пластинка толщиной h = 1 мм. Свет падает на пластинку нормально. На какой угол j следует повернуть пластинку, чтобы оптическая длина пути изменилась на l/2? Показатель преломления стекла n ст = 1,5.
Ответ: j = 1,72°.
Вариант 3
1. Какие волны называются когерентными?
2. Что называется оптической длиной пути?
3. Выведите условия возникновения интерференционных максимумов и минимумов.
4. Что называется показателем преломления?
5. Задача. На пути световой волны, идущей в воздухе, поставили стеклянную пластинку толщиной h = 1 мм. На сколько изменится оптическая длина пути, если волна падает на пластинку:
1) нормально;
2) под углом I = З0°.
Ответы: 1) увеличится на 0,5мм; 2) увеличится на 0,548 мм.
Лабораторная работа №3-02






