Комплексные числа и многочлены.
Понятие комплексного числа и его изображение на плоскости. Различные формы записи комплексных чисел. Операции над комплексными числами. Основная теорема алгебры. Теорема Безу. Разложение многочлена на множители.
Матрицы и определители
Матрицы и действия над ними. Определитель порядка n. Минор и алгебраическое дополнение. Вычисление определителей. Обратная матрица. Решение матричных уравнений.
Основные математические структуры.
Бинарные операции. Группы. Кольца, поля. Линейные пространства. Линейная зависимость и независимость систем векторов. Базис, координаты, размерность линейных пространств. Подпространства линейного пространства. Пересечение подпространств, прямая сумма подпространств. Линейная оболочка системы векторов. Изоморфизм линейных пространств. Ранг матрицы. Теорема о базисном миноре и ее следствия. Метрические и нормированные пространства. Пространства со скалярным произведением (унитарные), гильбертовы пространства. Алгебра геометрических векторов (векторная алгебра). Скалярное, векторное, смешанное произведения геометрических векторов.
Функции в линейных пространствах
Функции или отображения. Частные случаи отображений. Суперпозиция операторов (сложная функция), обратные операторы. Функции комплексного переменного. Линейные операторы. Область значений и ядро линейного оператора. Матрица линейного оператора. Матрица сложного линейного оператора. Матрица оператора обратного линейному оператору. Матрица перехода от одного базиса к другому. Связь между координатами вектора в разных базисах. Переход от ортонормированного базиса к ортонормированному базису. Ортогональные матрицы и их свойства. Изменение матрицы линейного оператора при изменении базиса.
Теория систем линейных уравнений
Основные задачи теории систем линейных уравнений. Различные формы записи системы линейных уравнений (полная, векторная, матричная). Классификация систем. Теорема Кронекера - Капелли. Теорема о наложении решений. Решение определенных систем. Матричный способ решения систем линейных уравнений. Метод Крамера, метод Гаусса. Исследование и решение произвольных систем линейных уравнений. Решение однородных систем. Структуры общего решения однородных и неоднородных систем.
Инвариантные подпространства линейного оператора. Собственные числа и собственные векторы линейного оператора. Диагонализация матрицы линейного оператора.
Линейные операторы в унитарном и гильбертовом пространствах
Линейные операторы в унитарном и гильбертовом пространствах (сопряженные и самосопряженные (симметричные) линейные операторы). Линейные и билинейные функционалы (формы). Теоремы об их общем виде в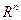 
. Квадратичные функционалы (формы). Приведение квадратичных форм к каноническому виду. Положительно определенные квадратичные формы. Условия положительной определенности.
Аналитическая геометрия
Общая теория кривых на плоскости, поверхностей и кривых в пространстве. Кривые и поверхности первого порядка: Прямая на плоскости. Плоскость и прямая в пространстве. Гиперплоскости и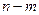 
мерные плоскости в 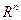. Кривые и поверхности второго порядка. Приведение уравнения кривой второго порядка к каноническому виду. Геометрическая интерпретация совокупности решений систем линейных уравнений.
Основная литература.
1. Бугров Я.С. Высшая математика: учебник для вузов: В 3 т. / Я.С. Бугров, С.М. Никольский; ред. В.А. Садовничий. Т. 1: Элементы линейной алгебры и аналитической геометрии.- 8-е изд., стереотип. - М.: Дрофа, 2006. - 284[4] с. (31 экз.)
2. Бугров Я.С. Высшая математика: учебник для вузов: В 3 т. / Я.С. Бугров, С.М. Никольский; ред. В.А. Садовничий. Т. 2: Дифференциальное и интегральное исчисление.- 7-е изд., стереотип. - М.: Дрофа, 2005. - 509[2] с. (31 экз.)
3. Магазинников Л.И. Высшая математика I. Практикум по линейной алгебре и аналитической геометрии: Учебное пособие / Л.И. Магазинников, А.Л. Магазинникова; Министерство образования Российской Федерации, Томский государственный университет систем управления и радиоэлектроники. - Томск: ТУСУР, 2007. - 163 с. (100 экз.).
4. Магазинников Л.И. Высшая математика. Линейная алгебра и аналитическая геометрия: учебное пособие / Л.И. Магазинников, А.Л. Магазинникова; Министерство образования Российской Федерации (М.), Томский государственный университет систем управления и радиоэлектроники (Томск). - Томск: ТМЦДО, 2003. - 176 с. (174 экз.).
5. Ельцов А.А. Высшая математика I. Дифференциальное исчисление. Учебное пособие для вузов /, Г.А. Ельцова, Л.И. Магазинников; Министерство образования Российской Федерации, Томский государственный университет систем управления и радиоэлектроники. - 2-е изд., перераб. и доп. - Томск: ТУСУР, 2001. - 227 с. (326 экз.).
