Расстояние от точки до прямой

Расстояние d от точки М(х₁; у₁) до прямой Ax+By+C=0 вычисляется по формуле

Эллипс уравнение:

, где b² = а ² – с ² Эксцентриситет: (0;Х) , где (0;У) Гипербола Уравнение: , где b ² = c ² – a ²

Эксцентриситет: Очевидно, что е > 1. Гипербола имеет две асимптоты, уравнения которых: ОУ уравнение ГИПЕРБОЛЫ

Эксцентриситет

Пример 1. Пусть требуется вычислить

Решение: f (x) = x ³ – 2 x – 3 и g (x) = x ² + 3 x + 3. Так как g (3) = 3² + 3 ∙ 3 + 3 = 21 ≠ 0. то имеем:

Пример 2. Вычислить .

Решение: здесь ƒ (2) = 2² - 5∙2 + 6 = 0, g (2) = 2² - 6∙2 + 8 = 0. Так как x ≠ 2, имеем

.

Пример 3. Вычислить .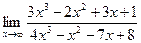

Решение .

Пример 4. Вычислить .

.

Пример 5. Вычислить .

Решение: .

Пример 6. Вычислить . Пример7. Найти предел .

= = = =0

Пример 8. Вычислить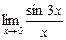

Решение: , заменяя 3 x = y и учитывая, что y → 0 при

x → 0, получаем: .

Пример 9. Вычислить .

Решение:

Пример 10. Вычислить

Решение:

 

Примеры по выполнению практической работы

Пример 1. Найти предел функции f(x) = |x| при x®0

Данная функция определена на всей числовой прямой. Так как f(x)=-x для х, удовлетворяющих неравенству x<0, то 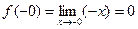.Так как f(x)=x, при x>0 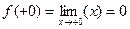.Таким образом, f(+0)=f(-0)=0. Так как односторонние пределы в точке нуль совпали, то предел функции f(x) в точке нуль существует и равен их общему значению, т.е.: .

Пример 2. Доказать, что функция не имеет предела в точке х=1.

Данная функция определена на всей числовой прямой. Вычислим односторонние пределы этой функции в точке х=1: , .

Итак, f(1-0)¹f(1+0). Следовательно, данная функция не имеет предела в точке х=1.

Пример 3. Исследовать на непрерывность функцию 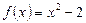в точке .

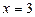Решение: воспользуемся определением 1:

1) Т.к. 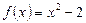определена на всей числовой прямой, то условие 1) выполнено;

2) ; ;

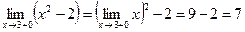значит предел функции 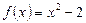в точке 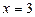существует и .

3) ;

Отсюда имеем, что , т.е. предел функции при равен значению функции при 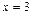. Следовательно, функция в точке х=3 непрерывна.

Пример 4. Исследовать на непрерывность функцию в точке .

Решение: опять воспользуемся определением 1:

1) в точке функция не определена, значит нет выполнения первого условия, и непрерывности в точке нет.

Пример 5. Исследовать на непрерывность функцию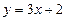

Решение: функция 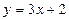определена на всей числовой оси. В таких случаях удобно для исследования на непрерывность пользоваться вторым определением.

Дадим аргументу приращение и найдем приращение функции :

 

Найдем предел при :

Т.к. равенство справедливо при любом конечном значении , поэтому функция непрерывна при любом значении .

Таблица производных элементарных функций

Правила дифференцирования

1.

2. ,

3. , ;

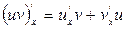4. ,

Пример по выполнению практической работы

Пример 1. Вычислить, если.

Решение:

Пример 2. Вычислить , если

Решение:

Пример 3. Вычислить , если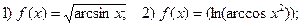

Решение:

;

2) данная функция является суперпозицией трех функций, поэтому имеем

Геометрическое приложение производной 1).y' (x₀) = tg α 2). y - y₀ = y ’(x₀) (x - x₀) 3).x = x₀. (3