Пример МАТРИЦЫ
Пример 1.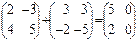 
Пример 2. 
Пример 3. 
.
Пример 4. Найти определитель матрицы 
.
Решение: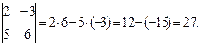 
Пример 5. Вычислить определитель
Ответ: D=4.
Пример 7. Найти А 
, если 
Решение: 
Составим союзную матрицу. Для этого вычислим алгебраические дополнения:
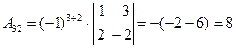
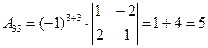
Союзная матрица будет следующей: 
. Вычислим обратную матрицу:
Проверкой 
убеждаемся, что обратная матрица найдена верно.
Пример ОБРАТНЫЕ МАТРИЦЫ.СИСТЕМЫ УРАВНЕНИЙ.
Пример 1. Решить систему уравнений методом обратных матриц:
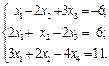
Решение: 
Составим союзную матрицу. Для этого вычислим алгебраические дополнения:
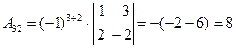
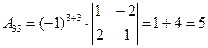
Союзная матрица будет следующей: 
.
Вычислим обратную матрицу:
Найдем решение системы по формуле (6):
.
решение(1; 2; -1)
Пример МЕТОД КРАМЕРА
Пример 1. Решить систему методом Крамера:
3x1 + x2 – 2x3 = 6;
5x1 – 3x2 + 2x3 = -4;
4x1 – 2x2 – 3x3 = -2.
Находим главный определитель системы:
3 1 -2
∆ = 5 -3 2 = 3∙(-3) ∙ (-3) + 1∙ 2∙ 4 + 5∙(-2) ∙ (-2) – 4∙(-3) ∙ (-2) – 5∙ 1∙(-3) –
4 -2 -3 - (-2) ∙ 2∙ 3 =27 +8 +20 -24 + 15 + 12 = 58.
Так как главный определитель системы не равен нулю, то она совместна. Находим определители: ∆x1, ∆x2, ∆x3. Определитель ∆x1 получается из главного определителя ∆ путём замены в нём первого столбца на столбец свободных членов.
6 1 -2
∆x1 = -4 -3 2 = 54 – 4 – 16 + 12 – 12 + 24 = 58.
-2 -2 -3
Т.к. ∆x1 отличен от нуля, значит решение системы единственное. Определитель ∆x2 получается из главного определителя ∆ путём замены в нём второго столбца на столбец свободных членов.
3 6 -2
∆x2 = 5 -4 2 = 36 + 48 + 20 – 32 + 90 + 12 = 174.
4 -2 -3
Определитель ∆x3 получается из главного определителя ∆ путём замены в нём третьего столбца на столбец свободных членов.
3 1 6
∆x3 = 5 -3 -4 = 18 – 16 – 60 + 72 + 10 – 24 = 0.
4 -2 -2
По формулам Крамера: x1 = 
= 
=1; x2 = 
= 
3; 
= 
= 0.
Итак, решением системы будет тройка чисел (1; 3; 0).
Пример МЕТОД ГАУСА
Пример 1. Решить систему методом Гаусса:
Решение: в результате элементарных преобразований над расширенной матрицей
системы:
Исходная система свелась к ступенчатой:
Поэтому общее решение системы: 
Если положить, например, 
найдем одно из частных решений этой системы 
Пример 2. Решить систему методом Гаусса:
Решение. Произведем элементарные преобразования над строчками расширенной матрицы системы:
Полученная матрица соответствует системе
Осуществляя обратный ход, находим 
Краткие теоретические и учебно-методические материалы по теме практической работы
Операции над векторами и их свойства Сложение векторов. Для того чтобы построить сумму двух данных векторов 
, нужно выбрать произвольную точку А и отложить от нее вектор 
, а затем от точки В отложить вектор 
. Тогда вектор 
является искомой суммой: 
Этот способ построения называется правилом треугольника.
Сумму двух данных векторов 
и 
можно построить и следующим образом. Откладывая от произвольной точки О векторы 
и 
, построим параллелограмм ОАСВ.
Тогда вектор 
(где 
– диагональ параллелограмма) является искомой суммой:
. Этот способ построения называется правилом параллелограмма:
Вычитание векторов. Два вектора называются противоположными, если их сумма равна нулевому вектору. Вектор, противоположный вектору , обозначают - . Таким образом, 
. Ненулевые противоположные векторы имеют равные длины и противоположные направления. Вектор с называется разностью векторов и , если 
. Чтобы вычесть из вектора вектор , достаточно прибавить к вектору вектор, противоположный вектору , т.е. 
Умножение вектора на число. Произведением ненулевого вектора на числоm называется вектор, имеющий направление вектора , если 
, и противоположное направление, если 
. Длина этого вектора равна произведению длины вектора на модуль числа m. Произведение вектора на число m обозначается m . При любых m и векторы m и коллинеарны и 
. Угол между двумя векторами. Угломмеждудвумя ненулевыми векторами и называется угол между направлениями этих векторов: 
, где 
.
Частные случаи: 1) если 
, то 
; 2) если 
, то 
.
Декартова система координат Пусть на плоскости задана пара единичных взаимно перпендикулярных векторов 
и 
, отложенных от некоторого начала – точки О. Такую пару векторов называют прямоугольным базисом на плоскости. Совокупность начала О и прямоугольного базиса 
называют прямоугольнойсистемойкоординат на плоскости. Точку О называют началом координат, а векторы (1; 0) и (0; 1) – координатными векторами. Вектор, направленный из начала координат в произвольную точку М плоскости xOy, называется радиусом–вектором точки М и обозначается 
: 
Проекции вектора на координатные оси, т.е. 
и 
, называются координатами вектора. Координаты вектора кратко записывают так: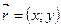 
.Координаты радиуса-вектора 
являются одновременно координатами точки M, т.е. конца радиуса вектора. Если начало вектора 
не совпадает с началом координат, то координаты вектора и координаты его конца различны. В этом случае проекции вектора на оси координат соответственно равны 
и 
, т.е.: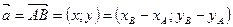 
:
Разложение вектора по координатным осям. Разложение вектора 
в базисе имеет вид 
, Действие над векторами в координатах
Пустьв базисе заданы векторы 
и 
, тогда координаты суммы двух (или более) векторов равны суммам соответствующих координат слагаемых, т.е.
координаты разности двух векторов равны разностям соответствующих координат этих векторов, т.е. 
координаты произведения вектора на число равны произведениям соответствующих координат данного вектора на это число, т.е. 
Длина вектора 
находится по формуле 
Длина вектора 
находится по формуле 
.С помощью этой формулы вычисляется также расстояние между двумя точками на плоскости. Скалярным произведением двух векторов называется число, равное: 
Скалярное произведение двух ненулевых векторов, с другой стороны, может быть найдено как произведение модулей этих векторов на косинус угла между ними:
. Скалярным квадратом вектора называется скалярное произведение 
. Скалярный квадрат вектора равен квадрату его длины.
Условие коллинеарности двух векторов Условие коллинеарности двух векторов и 
имеет вид 
,
т.е. если соответствующие координаты двух векторов пропорциональны, то векторы коллинеарны.
Общее уравнение прямой Ax+By+C=0,
| Значение коэффициентов | Уравнение прямой | Положение прямой |
| С=0 А=0 В=0 А=0, С=0 В=0, С=0 | Ах+Ву=0 у=b, где b= -С / В x=a, где a= -C / A y=0 x=0 | Проходит через начало координат Параллельна оси Ох Параллельна оси Оу Совпадает с осью Ох Совпадает с осью Оу |
Угловой коэффициент прямой y=kx+b Угловой коэффициент k прямой, заданной уравнением Ax + By + C =0, находится как коэффициент k прямой, заданной двумя точками А(ха; уа) и В(хВ;уВ), вычисляется по формуле: 
Уравнение прямой в отрезках Уравнением прямой в отрезках называетсяуравнение вида: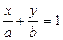 
Уравнение прямой, проходящей через точку в данном направлении
Уравнение прямой, проходящей через т.у А(ха; уа) и имеющей угловой коэффициент k, записывается в виде у – уа=k (x – xa Уравнение прямой, проходящей через две точки. Уравнение прямой, проходящей через две точки т. А (х1; у1) и т. В (х2; у2), имеет вид
Нормальное уравнение прямой А(х-хо)+В(у-уо)=0 Угол между прямыми. Условие параллельности 2-х прямых: 
Условие перпендикулярности 2-х прямых: 
Условие параллельности в этом случае имеет вид: 
Условие перпендикулярности прямых: 
Если две прямые заданы каноническими уравнениями: 
и 
то угол φ между этими прямыми определяется по формуле:
Условие параллельности прямых: 
Условие перпендикулярности прямых: 
