перпендикуляр түзуді проекциялаушы деп атайды.
Проекциялаушы түзудің қандай да бір проекциясының нүкте
болуы - оның негізгі белгісі. Проекциялаушы түзу былай деп
аталады:
- горизонталь-проекциялаушы, егер ол π 2 проекция
жазықтығына перпендикуляр болса (3.6 а -сурет);
- фронталь-проекциялаушы, егер ол π 1 проекция
жазықтығына перпендикуляр болса (3.6 ә -сурет);
- профиль-проекциялаушы, егер ол π 3 проекция
жазықтығына перпендикуляр болса
(3.6 б -сурет).
26.Жалпы жағдайда орналасқан жазықтық және дербес жағдай жазықтықтары деп қандай жазықтықтарды айтады?
Жалпы жағдайда жазықтықтың үш ізі болады: горизонталь ha, фронталь fa, профиль pa. Жазықтықтың іздері қосарланып осьтермен жазықтық іздерінің тоғысу нүктелері деп аталатын Xa, Ya, Za нүктелерінде қиылысады. Жазықтық іздерінен пайда болған үшбұрыш іздер үшбұрышы деп аталады. Проекциялар жазықтықтарына қатысты олардың біреуіне де перпендикуляр болмайтын жазықтық жалпы жағдайдағы жазықтық деп аталады.
Дербес жағдайлар кезінде:
Проекциялаушы жазықтықтар: фронталь проекциялаушы, горизонталь проекциялаушы және профиль проекциялаушы жазықтықтар деп аталады. Егер жазықтық проекциялар жазықтықтарының біреуіне перпендикуляр болып, екіншісіне параллель болмаса, ондай жазықтықты проекциялаушы жазықтық деп атайды.
Егер жазықтық фронталь проекциялар жазықтығына перпендикуляр, горизонталь проекциялар жазықтығына параллель орналаспаса, ондай жазықтықты фронталь проекциялаушы жазықтық деп атайды
27.Фронталь бәсекелс, горизонталь бәсекелес нүктелер деп қандай нүктелерді айтады?
Бір проекциялаушы түзуде орналасқан нүктелерді бәсекелес нүктелер деп айтамыз. Горизонталь проекциялаушы түзудің бойындағы нүктелер горизонталь бәсекелес, фронталь проекциялаушы түзудің бойындағы нүктелер фронталь бәсекелес болады.
28 Эпюрде көрінетіндікті қалай анықтайды?
π 2 жазықтығын x осінен айналдырып, π 1 жазықтығымен
беттестірейік. Сонда пайда болған кескін Монж эпюрі деп
аталады (3.1 ә -сурет). Эпюрде А нүктесінің А 1 және А 2
проекциялары x осіне перпендикуляр түзудің бойында
орналасады. А 1 А 2 түзуі байланыс сызығы деп аталады. Бұндай
сызба қайтымды болып табылады, себебі онда А нүктесінің
координаталарын анықтауға болады.
29.Көпжақтың анықтамасын беріңіз
Жазық көпбұрыштармен шектелген денелердi көпжақтар дейдi. Олардың жазық көпбұрышын жақ деп, өзара қиылысу түзулерiн қыр деп атайды. Көпжақтар дұрыс және дұрыс емес болып екiге бөлiнедi. Дұрыс көпжақтардың барлық жақтары, қырлары және бұрыштары өзара тең болады. Платон денелерi деп аталатын бес дұрыс көпжақтар бар, олар:
− тетраэдр (төрт жақты), жақтары тең қабырғалы төрт үшбұрыштан тұрады;
− гексаэдр (алты жақты), жақтары алты шаршыдан тұрады;
− октаэдр (сегiз жақты), жақтары тең қабырғалы сегiз үшбұрыштан тұрады;
− икосаэдр (жиырма жақты), жақтары тең қабырғалы жиырма үшбұрыштан тұрады;
− додекаэдр (он екi жақты), жақтары дұрыс он екi бесбұрыштан тұрады.
Сызбада көпжақ − төбесiнiң және қырларының проекциялары арқылы берiледi, немесе олардың проекцияларын тұрғызу нүктенiң және түзудiң кесiндiлерiн тұрғызу арқылы орындалады. Көпжақтардың iшiнде көбiрек тарағандары жәй көпбұрыштардан тұратын пирамида және призма түрлерi.
30.Көпжақтың жазықтықпен қиылысу сызығын анықтау әдістерін атаңыз
Көпжақ пен жазықтықтың қиылысуынан пайда болған көпбұрышты қима дейдi. Көпбұрыштың төбесi көпжақтың жазықтықпен қиылысқан қырларының санына тең. Сондықтан көпбұрыштың төбелерi қырлардың жазықтықпен қиылысу нүктелерi болып келедi. Мысалы, төртбұрышты пирамиданың қимасы үшбұрыш, төртбұрыш не бесбұрыш болуы мүмкiн.
Көпжақты бет жазықтықпен қиылысқанда пайда болатын қима - қырлар және жақтар деп аталатын екi тәсiлдiң бiрiмен тұрғызылады. Қырлар тәсілімен тұрғызуда түзу мен жазықтықтың өзара орналасу есебiнiң шешiмi бiрнеше рет қайталанады. Мұнда түзудiң орнына көпжақтың қырлары қатынасады. Екiншi тәсiлде екi жазықтықтың өзара орналасуын анықтайтын есептiң шешiмi қолданылады. Екiншi тәсiлдi қолдану, көпжақтың жақтары проекциялаушы жағдайда орналасса өте ыңғайлы болады. Қалған жағдайларда қырлар тәсiлi тиiмдi болып келедi.
Көпжақ бетінің жазықтықпен қимасы – жазық көпбұрыш болып табылады. Оның төбелері мен қабырғалары – берілген жазықтықтың берілген көпжақтың жақтарымен және қырларымен қиылысуымен анықталады. Сондықтан қиманы тұрғызу үшін екі түрлі тәсіл қолданылады:
1) қырлар тәсілі – берілген жазықтықтың көпжақ қырларымен қиылысу нүктелерін, яғни қиманың төбелерін табады;
2) жақтар тәсілі – жазықтықтың көпжақ жақтарымен қиылысу түзулерін, яғни қиманың қабырғаларын тұрғызады. Жақтар тәсілін көпжақ жақтарының проекциялаушы жазықтықтар болған кезінде қолданған тиімді. Көпжақтың жазықтықпен қимасын табуға бірнеше мысалдар қарастырып көрелік.
31 Қандай есептер метрлік деп аталады. Кесіндінің нақты шамасын қалай табады
Метрикалық есеп деп өлшемдерді анықтаумен байланысты есептерді айтамыз. Метрикалық есептерде арақашықтық, бұрыштың шамасы, геометриялық фигуралардың аудандарының натурал шамалары анықталады. Метрикалық есептерді шешу үшін өзара перпендикуляр түзулер мен жазықтықтарды салуға тура келеді.
32 Эпюрді түрлендіру деп нені айтамыз?
Нүктенiң эпюрi.
Бiр жазықтықтағы бiр проекциядан тұратын кескiн қайтымы болмайтындықтан, өзара перпендикуляр p1 және p2 жазықтықтарын алып, берiлген А нүктесiн осы жазықтықтарға тiк бұрыштап проекциялаймыз (3.1, а-сурет).
.1-суретp1 жазықтығыналдымыздакөлденеңжәне тiк орналастырып, он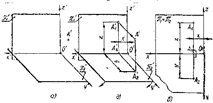 
ы фронтальпроекцияларжазықтығы депатаймыз. p2 жазықтығын горизонталь орналастырамыз, сондықтан оны горизонталь проекцияларжазықтығы депатаймыз. p1 жәнеp2 жазықтықтарыныңқиылысусызығынпроекцияларосiдепатайды: х=p1Çp2. Анүктесiнiңp1 жазықтықтағытiкбұрыштыпроекциясын (А1нүктесiн) оныңфронтальпроекциясы, алp2 жазықтығындағытiкбұрыштыпроекциясын (А2нүктесiн) оныңгоризонтальпроекциясыдепатайды. Анүктесiненхосiнетүсiрiлгенперпендияулярдыңтабаны (Ахнүктесi) оның осьтiяпроекциясыболады. СондаА, А1, АхжәнеА2 нүктелерiтiкбұрыштытөртбұрыштыңтөбелерiндеорналасады. Жазықкескiналуүшiнp2 жазықтығыноныңp1 жазықтығыменқиылысусызығынанайналдырып, олардыбеттестiремiз: p1=p2. СондапайдаболғанкескiндiМонжэпюрi, қысқашаэпюрдепатайды (3.1, б-сурет). Эпюрфранцуздың “жазықсызба” дегенмағынадағысөзiнен алынған. Онданүктенiңфронталь (А1) жәнегоризонталь (А2) проекциялары (хосiнеперпендикуляр) вертикальбайланыссызығыбойыншаорналасады: (А1А2)^х. (А1А2) – вертикальбайланыссызығы. Координаталарыбелгiлiнүктенiңэпюрiнсалуоңай, өйткенi |O'Аx'|=|OAx|=x, |Ax'А2'|=|AxA2|=y, |Ax'А1'|=|AxA1|=z.
33Проекция жазықтығын алмастыру әдісімен жазықтықтың нақты шамасын қалай анықтайды?
Проекциялар жазықтығын алмастыру тәсiлi А нүктесiнiң фронталь p1 және горизонталь p2 жазықтықтар жүйесiндегi проекцияларын қарастыралық (5.1,а-сурет). Фронталь проекциялар жазықтығын горизонталь проекциялаушы p4 жазықтығымен алмастыралық. p4^p2;p2Çp4=x24;p1Çp2=x12. Берiлген А нүктесiн p4 жазықтығына тiк бұрыштап проекциялалық: (АА4)^p4.
5.1-сурет
Ендi p2 жазықтығын p4 жазықтығымен алмастыруды қарастырылады. Алдыңғы жағдайда горизонталь проекциялар жазықтығы p2 сақталса, қарастырылып отырған жағдайда фронталь проекциялар жазықтығы p1 сақталады. p4^p1;p1Çp4=x14. Эпюр алуүшiн p2 жазықтығынх12 түзуiнен, ал p4 жазықтығынх14 түзуiненайналдырыпp1 жазықтығыменбеттестiремiз. Эпюрде (А1А4)^х14 және |A4A14|=|А2А12|
Проекциялар жазықтығын алмастыру тәсiлiнiң инварианттары:
1) нүктенiң жаңа проекциясы мен сақталатын проекциясы жаңа өске прпендияуляр түзүдiң бойында орналасады;
2) нүктенiң жаңа проекциясынан жаңа өске дейiнгi қашықтық оның ескi проеяциясынан ескi өске дейiнгi қашықтыққа тең болады.
Жаңа проекциялар жазықтығын есептi шешуде қолайлы болатындай етiп таңдап алады. Егер проеяциялар жазықтықтарының бiреуiн алмастыру жеткiлiктi болмаса, онда екiншiсiнде бiртiндеп жаңа жазықтықпен алмастыруға болады
34.Қандай жағдайда тік бұрыштың тік бұрышты проекциясы тік бұрыш болады?
Егер жазық тік бұрыштың бір қабырғасы проекциялар жазықтығына параллель болып, ал екінші қабырғасы сол проекциялар жазықтығына перпендикуляр болмаса, онда тік бұрыш осы жазықтыққа тік бұрыш күйінде проекцияланады. Бұл теореманы тік бұрыштың тік проекциялау теоремасы деп аталады
Егер жазық бұрыштың қабырғалары проекциялар жазықтығына параллель болса, олардың арасындағы бұрыш сол проекциялар жазықтыққа нақты шамамен проекцияланады. Себебі мұндай жазық бұрыштың жазықтығы проекциялар жазықтығына параллель болып келеді. Сонымен мұндай жағдайда сүйір бұрыш сүйір күйінде, доғал бұрыш доғал күйінде, тік бұрыш тік күйінде ешбір өзгеріссіз проекцияланады. Егер бұрыштың қабырғалары кеңістікте жалпы жағдайда орналасса, немесе проекциялар жазықтығына параллель болмаса, онда бұрыш өзгеріп проекцияланады.
35 Нүктеден h горизонтальға перпендикуляр түзуді қалай жүргіземіз?
Түзу мен жазықтық өзара перпендикуляр болса, онда түзудің фронталь проекциясы жазықтықтың фронталь түзуінің фронталь проекциясына, оның горизонталь проекциясы жазықтықтың горизонталь түзуінің горизонталь проекциясына перпендикуляр болады.
Теорема жоғарыда қарастырылған өзара перпендикуляр түзулер арқылы дәлелденеді.
36Нүктеден f фронтальға перпендикуляр түзуді қалай жүргіземіз? 1-салдар. Өзара перпендикуляр екі түзудің біреуі горизонталь болса, олардың горизонталь проекциялары өзара перпендикуляр болады. (6.1 а -сурет).
2-салдар. Өзара перпендикуляр екі түзудің біреуі фронталь болса, олардың фронталь проекциялары өзара перпендикуляр болады. (6.1 ә -сурет).
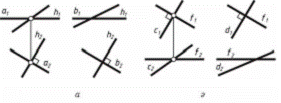
3-салдар. Өзара перпендикуляр екі түзудің біреуі профиль түзуі болса, олардың профиль проекциялары өзара перпендикуляр болады.
