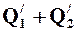Плоские задачи теории установившейся фильтрации. Интерференция скважин.

 

Если давление и скорость фильтрации зависят только от двух координат и в каждой плоскости, перпендикулярной к третьей оси, поле скоростей и давлений одинаково, то фильтрационный поток можно считать плоским. Плоский фильтрационный поток имеет место при работе одной или нескольких скважин, как нагнетательных, так и эксплуатационных в однородном горизонтальном пласте постоянной мощности.

При работе нескольких скважин в пласте происходит взаимное влияние их друг на друга, называемое интерференцией скважин.

Потенциалом течения называется функция, производная от которой взятая вдоль линии тока и с противоположным знаком, совпадает с вектором скорости:

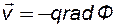(6.1)

Из сравнения (6.1) с законом Дарси (2.5) видно, что для несжимаемой жидкости:

(6.2)

Для плоскорадиального потока можно получить следующее выражение для потенциала точечного стока (источника):

(6.3)

где: 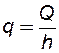- удельный дебит скважины-стока приходящийся на единицу мощности пласта, С – постоянная интегрирования.

Если q > 0, то выражение (6.3) определяет распределение потенциала от стока - добывающей скважины, если q < 0, то выражение (6.3) определяет распределение потенциала от источника – нагнетательной скважины.

Нетрудно заметить, что в точках r =0 и потенциал не имеет смысла.

Распределение потенциала (давления) для несжимаемой жидкости (6.3) удовлетворяет уравнению Лапласа, которое для плоских течений имеет вид:

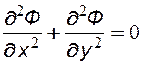- в декартовой системе координат (6.4)

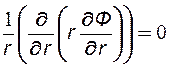- в случае осевой симметрии (6.5)

Метод суперпозиции. Опираясь на основные свойства решений уравнения Лапласа в силу его линейности и однородности, был разработан метод суперпозиции (метод наложения решений).

Гидродинамический смысл метода суперпозиции состоит в том, что изменение пластового давления или потенциала Ф_М в любой точке пласта М, вызванное работой каждой скважины (Ф₁, Ф₂, Ф₃,… Ф_n) (нагнетательной или добывающей), подсчитывается так, как если бы данная скважина работала в пласте одна, независимо от других скважин. Затем эти независимо определенные для каждой скважины изменения давления или потенциала в каждой точке пласта алгебраически суммируются:

(6.6)

Суммарная скорость фильтрации 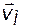в точке М определяется как векторная сумма скоростей фильтрации , вызванных работой каждой скважины в отдельности, рис. 14:

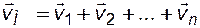(6.7)

где .

	(б)

 

Рис.14. Схема скоростей фильтрации в точке М при работе скважин стоков (а) и результирующий вектор 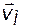в точке М (б)

 

Для определения дебитов или забойных потенциалов n скважин, работающих в пласте с удалённым контуром питания можно считать, что потенциал на контуре питания Ф_к и радиус самого контура питания R_к известны и одинаковы для всех скважин. Используя принцип суперпозиции, поместив точку М на забой каждой скважины и на контур питания (рис.15), можно получить следующую систему уравнений:

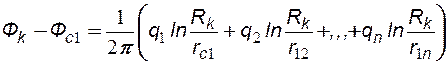
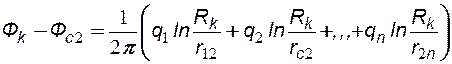(6.8)

………………………………………………………..

где: r_Сi - радиус скважины на которую помещена точка М; r_ji -расстояние между I -й и j -й скважинами; Ф_Сi - забойный потенциал i-ой скважины, при этом r_ji = r_ij, r_ji << R_к, r_сi << r_ij при I ¹ j.

Переходя от потенциалов к давлению при помощи системы уравнений (6.8) можно решать задачи двоякого рода: или находить депрессию при заданном дебите, или, если заданы депрессии, то, решая эту систему, получить значения дебитов. Положительные значения дебитов будут для эксплуатационных скважин (стоков), отрицательные - для нагнетательных скважин (источников). После того как дебиты найдены, пластовое давление в любой точке определяется из формулы (6.6), причем результат тем точнее, чем дальше эта точка отстоит от контура питания.

Метод отображения источников (стоков). Используется в случае пластов, имеющих контур питания или непроницаемую границу произвольной формы. При этом для выполнения тех или иных условий на границах вводятся фиктивные стоки или источники за пределами пласта, получаемые зеркальным отображением реальных относительно границы. Фиктивные скважины, в совокупности с реальными обеспечивают необходимые условия на границах, и задача сводится к рассмотрению одновременной работы реальных и фиктивных скважин в неограниченном пласте.

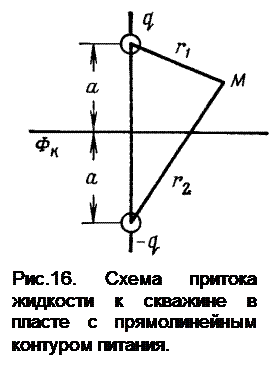
Например, если эксплуатационная скважина (сток) с удельным дебитом q находится в пласте с прямолинейным контуром питания на расстоянии а от контура, то её надо зеркально отобразить относительно контура, т.е. поместить фиктивную скважину с другой стороны от контура на расстоянии а и считать её дебит отрицательным -q (скважина-источник), рис.16. При этом потенциал в любой точке М (по методу суперпозиции) равен:

(6.9)

На контуре питания r₁ = r₂, тогда Ф_к = С. То есть теперь условие постоянства потенциала на контуре питания выполняется.

Поместим точку М на стенку скважины, тогда r₁ = r_с и r₂» 2 а, а удельный и объемный дебиты скважины определяется по формулам:

(6.10)

При помощи метода отображения источников и стоков также можно определить дебит скважины, эксцентрично расположенной в круговом пласте:

(6.11)

где e – расстояние от центра скважины до центра кругового пласта (эксцентриситет).

Метод эквивалентных фильтрационных сопротивлений Ю.П. Борисова. Этот метод основан на аналогии движения жидкости в пористой среде с течением электрического тока в проводниках. Рассматривается задача о притоке жидкости к одной бесконечной цепочке скважин, расположенных на расстояниях 2 а друг от друга и на расстоянии L от прямолинейного параллельного ей контура питания. На контуре питания задан постоянный потенциал Ф_к, а на забоях скважин - потенциал Ф_с (рис. 17).

Цепочка скважин-стоков (галерея) отображается зеркально относительно параллельного ей контура питания в скважины-источники, и рассматри-вается интерференция двух цепочек скважин в неограниченном пласте. Вдоль прямой АВ, проходящей через скважину (как говорят, вдоль главной линии тока), частицы жидкости будут двигаться наиболее быстро. Прямые А'В', делящие расстояние между скважинами пополам, в силу симметрии потока, можно рассматривать 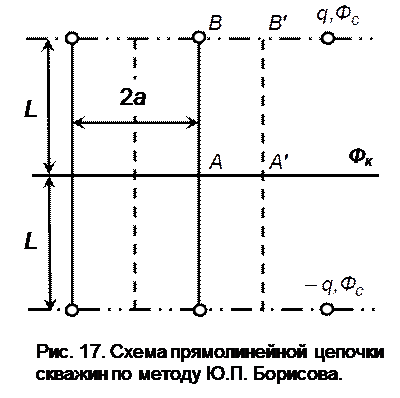как непроницаемые гра-ницы, вдоль которых движе-ние будет наиболее мед-ленным; они называются нейтральными линиями тока. Задача решается методом суперпозиции. Результаты решения пока-зывают, что на расстоянии от контура до половины расстояния между скважи-нами движение жидкости практически прямолинейное и падение потенциала на этом участке происходит по закону прямолинейной

фильтрации. Основное падение потенциала происходит вблизи скважины в зоне радиусом , где характер движения близок к радиальному. При этом удельный дебит каждой скважины цепочки при условии, что L > a, выражается следующей формулой: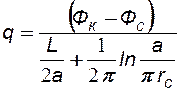

(6.12)

Суммарный дебит всей прямолинейной цепочки из n скважин:

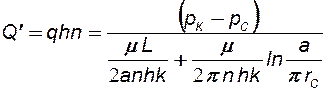(6.13)

Введем обозначения:

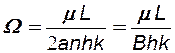(6.14)

где - назовем внешним фильтрационным сопротивлением, выражающим сопротивление потоку жидкости от контура питания до галереи шириной ;

(6.15)

где - назовем внутренним сопротивлением, выражающим сопротивление, возникающее при подходе жидкости к скважинам, где фильтрация практически плоскорадиальная.

Представим формулу (6.13) в виде:

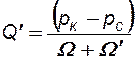, (6.16)

аналогичном закону Ома для полной цепи, где выполняет роль силы тока, а - разности потенциалов. Таким образом, приток жидкости к цепочке скважин можно представить электрической схемой эквивалентных фильтрационных сопротивлений, рис. 18.

Отметим, что приток жидкости к кольцевой батарее (скважины расположены по линии окружности, находящейся внутри кругового контура питания и имеющей с ним общий центр, рис.19), рассчитывается также по формуле эквивалентных фильтрационных сопротивлений (6.16).

Отличие будет лишь в определении внешнего сопротивления :

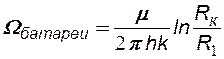(6.17)

где R₁ – радиус кольцевой батареи, рис.19

Такой метод позволяет решать практические задачи, когда на месторождении одновременно работают несколько прямолинейных цепочек скважин или кольцевых батарей.

 

 

 

Например, рассмотрим полубесконечный пласт с прямолинейным контуром питания, который разрабатывается тремя параллельными цепочками скважин одинаковой длины с числом скважин n₁, n₂, n₃ в каждой и суммарными дебитами , , 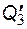. Пусть скважины в каждой цепочке имеют радиусы r_с1, r_с2, r_с3 и забойные давления р_с1, р_с2, р_с3.

Электрическая схема, соответствующая такой задаче, будет разветвленной (рис. 20), а ее расчет проводится по законам Ома и Кирхгофа.

При этом, составляются алгебраические линейные уравнения по числу неизвестных. Например, для схемы, изображенной на рисунке 20, система уравнений примет вид:

(6.18)

где: , , 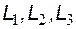- расстояния соответственно от контура питания до первой цепочки, между первой и второй цепочками, между второй и третьей цепочками.

 

Задачи к разделу 3

 

Задача 6.1

Совершенная скважина радиуса r_с = 0,1 м работает в пласте, ограниченном двумя непроницаемыми границами, расположенными под углом 90⁰. Расстояния до границ равны a = 150 м, b = 300 м, расстояние до контура питания R_к = 8 км, давление на границах (контурах питания) p_к = 11,76 МПа, давление на забое p_с = 9,8 МПа. Мощность пласта h = 12м, вязкость жидкости μ = 3 мПа∙с, проницаемость пласта k = 700мД. Найти дебит скважины.

 

Задача 6.2

В полубесконечном пласте мощностью h = 10 м с прямолинейным контуром питания работает совершенная добывающая скважина, расположенная на расстоянии a = 300 м от контура, с дебитом 50 т/сут. Определить скорость фильтрации:

а) у стенки скважины;

б) в точке А, расположенной на контуре питания и отстоящей на

b = 500м от места пересечения линии контура питания с перпендикуляром, опущенным из скважины на контур питания (см. рис.21);

в) в точке В, расположенной (под углом от скважины) на расстоянии c = 150 м от скважины вдоль перпендикуляра, опущенного из скважины на контур питания и

d = 200 м от этого перпендикуляра вдоль контура (см. рис.21).

 

Задача 6.3

Определить дебит батареи из четырех скважин, расположенных вдали от контура питания, и одной скважины, находящейся в центре (см. рисунок 22), если известно, что все скважины находятся на окружности радиуса R₁ = 200м (радиус батареи) на одинаковом расстоянии друг от друга и работают в одинаковых условиях. Расстояние до контура питания R_к = 10км, радиус скважин r_с = 0,1м, мощность пласта h = 10м, потенциал на контуре Ф_к = 40см²/сек, а на скважинах Ф_с = 30см²/сек.

Задача 6.4

Круговой нефтяной пласт радиусом R_к = 15км, мощностью h = 8м, эксплуатируется пятью скважинами радиусом r_c = 7,5 см, из которых четыре расположены в вершинах квадрата со стороной d = 150 м, а пятая в центре (рис. 22). Давление на контуре р_к = 11МПа, забойные давления на всех скважинах одинаковы и равны р_с = 90атм. Коэффициент проницаемости k = 0,6 Д, вязкость нефти m = 1,1 сПз.

Определить дебиты скважин и отношения дебитов Q₅/Q₁.

 

Задача 6.5

Определить забойное давление в скважине 1 с радиусом r_с =0,1м в круговом пласте с радиусом контура питания R_к =10км, если при забойном давлении в скважине 2 с тем же радиусом, расположенной на расстоянии 2а =150м от первой с забойным давлением р_с2 =6,82МПа, скважина 1 не дает нефти. Давление на контуре питания р_к =9,8МПа. Скважины 1 и 2 расположены симметрично относительно центра, рис.23.

 

 

Задача 6.6

Найти значения потенциалов на скважинах, расположенных симметрично на расстоянии 2 а =300 м относительно центра удаленного кругового контура питания (см. рис. 23) радиуса R_к =5 км, если известно, что дебит одной составляет 200 т/сут, а другой 300 т/сут, потенциал на контуре питания Ф_к =50 см²/сек, радиус скважины r_с =0,1 м, мощность пласта h =10м, плотность нефти r =0,85 т/м³.

 

Задача 6.7

В круговом пласте радиуса R_к = 200м работает эксцентрично расположенная скважина радиуса r_с = 0,1 м. Найти изменение дебита в зависимости от расположения скважины (эксцентриситета e) по отношению к дебиту скважины, расположенной в центре.

Задача 6.8

Определить суммарные дебиты нефти вязкостью m = 3сПз, параллельно расположенных трех цепочек скважин, эксплуатирующих прямоугольный пласт мощностью h = 3 м с проницаемостью k = 0,5 Д. Давление на контуре питания р_к =170 атм, забойные давления на всех эксплуатационных скважинах одинаковы и равны р_с1 = р_с2 = р_с3 =100 атм. Расстояния L₁ = 1500 м,, L₂ = L₃ =1000м.. Радиусы скважин одинаковы и равны r_c = 0,1 м. Число скважин в цепочках одинаково и равно n ₁ =n ₂ =n ₃ =5 Расстояние между скважинами в цепочках 2 а₁ =2 а₂ =2 а₃ =600м.

Указание: Задачу решать методом эквивалентных фильтрационных сопротивлений Ю. П. Борисова.

 

Задача 6.9

Определить дебиты скважин двух круговых батарей с радиусами R₁ =1000м и R₂ =600м, расположенных концентрично в круговом пласте с радиусом контура питания R_к =3500 м. Скважины радиусом r_с =10 см эксплуатируются при постоянных забойных давлениях р_с1 =100 атм, р_с2 =95 атм; давление на контуре питания р_к =125 ат; мощность пласта h =10 м; проницаемость пласта k =0,2 Д, вязкость нефти m =5 сПз. Число скважин в батареях n₁ = 10, n₂ = 6.

Указание: Задачу решать методом эквивалентных фильтрационных сопротивлений Ю. П. Борисова.

 

Задача 6.10

Определить дебиты скважин, расположенных тремя кольцевыми батареями методом Ю. П. Борисова. Давление на контуре питания р_к =170 ат, забойные давления на всех эксплуатационных скважинах одинаковы и равны р_с1 = р_с2 = р_с3 =120 атм. Радиусы батарей R₁ = 4000 м,, R₂ = 3500 м, R₃ =3000м.. Радиус скважину r_c =0,1 м, радиус контура области питания R_к =20 км. Расстояние между скважинами в батареях 2 а₁ =2 а₂ =2 а₃ =400 м; мощность пласта h = 10 м, проницаемость k = 0,2 Д; вязкость нефти m =3сПз.

 

Задача 6.11

Определить какому плоскому фильтрационному течению соответствует комплексный потенциал и найти распределение скорости фильтрации, линии равного потенциала и линии тока.