4.1. Определение
Под функцией двух переменных понимают отображение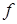 
, при котором каждой паре значений 
соответствует единственное значение 
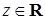. Обозначают такую функцию 
. Областью 
называется часть плоскости, ограниченная линиями. Линия, ограничивающая область, называется границей.
Определение. Область называется ограниченной, если существует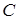 
– const такое, что расстояние от любой точки области до начала координат меньше C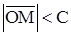 
Множество точек M(x;y) координатной плоскости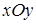 
, координаты которых удовлетворяют условию 
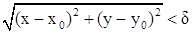или 
называется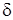 
- окрестностью точки 
(
). 
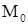Определение. Число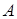 
называют пределом функции f(x;y) при 
, если для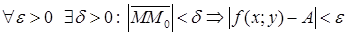 
и пишут 
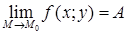или 
.
Если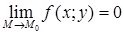 
, то функция 
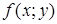называется бесконечно малой величиной.
Теорема. Пусть функци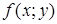и и 
определены в некоторой области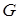 
и пусть существуют 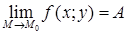и 
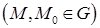тогда 
.
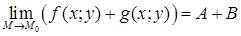
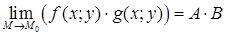
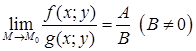Для функций нескольких переменных выполняются и другие свойства пределов.
Пусть точка 
принадлежит области определения функции 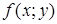. Определение. Функция называется непрерывной в этой точке, если 
или 
.
Определение. Функция непрерывная в каждой точке области называется непрерывной в области.
Рассмотрим функцию двух переменных и посмотрим, как изменяется функция при условии, что 
, а 
– переменная величина. 
. 
называется частичным приращением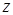 
по . Аналогично определяется частичное приращение функции по 
, при условии, что 
. Если придавать приращение обеим переменным, то получим полное приращение функции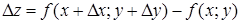 
.
4.2. Частные производные. Полный дифференциал
Частной производной функции по переменной называется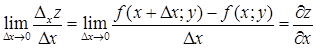 
.
Частной производной функции по переменной называется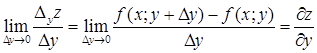 
.
Замечание. Так как частичное приращение 
вычисляется при условии, что , то производная вычисляется от функции, зависящей только от . Аналогично: частная производная функции по вычисляется в предположении, что переменная, а постоянная величины. Из вышесказанного следует, что вычисление частных производных производится по тем же правилам, что и вычисление производных функций, зависящих от одной переменной.
Замечание. Частные производные функций, зависящих от любого числа переменных, находятся аналогично.
Определение. Функция называется дифференцируемой в точке , если приращение ее может быть представлено в виде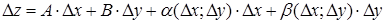 
.
Определение. Главная часть приращения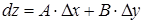 
называется полным дифференциалом.
Теорема 1. Если функция дифференцируема в точке , то она непрерывна в этой точке.
Теорема 2. Если функция дифференцируема, то существуют ее частные производные, причем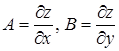 
.
Отсюда следует форма полного дифференциала: 
.
Теорема 3. Если функция имеет частные производные в некоторой окрестности точки и эти частные производные непрерывны в самой точке 
, то эта функция дифференцируема в точке
4.3. Касательная плоскость и нормаль к поверхности
Пусть функция дифференцируема в некоторой области . Рассмотрим поверхность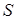 
в трехмерном пространстве, графиком которой является данная функция. Выберем точку 
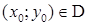и точку 
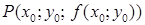, принадлежащую этой поверхности. Плоскости 
и 
пересекают поверхность 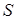по плоским линиям, проходящим через точку 
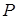. К этим плоским линиям через точку 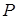можно провести касательные, которые определяют плоскость. Полученная плоскость называется касательной плоскостью к поверхности 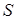. Прямая перпендикулярная к касательной плоскости и точке касания, называется нормалью к поверхности в этой точке.
Уравнения касательной плоскости и нормали находятся соответственно по формулам
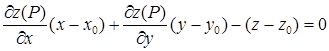и 
.
Если поверхность 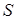задана неявным уравнением 
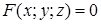, то касательная плоскость и нормаль к поверхности определяются уравнениями 
и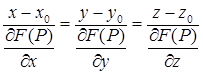 
.
