Поставленная в курсовой работе задача по аппроксимации функции, заданной таблично, была выполнена с помощью визуальной среды программирования Visual Basic 6.0
Сначала в приложении «Блокнот» был создан.txt файл, содержащий исходные данные. Его можно увидеть на рис. 7.

Рис.7
Текстовый файл находится в одном каталоге с проектом Visual Basic.
Далее с помощью стандартных блоков была составлена форма для визуализации программы аппроксимации функции, заданной таблично. После этого был введен код программы, представленный ниже.
Код программы:
' Описание переменных для процедуры решения СЛАУ
Dim A()
Dim B()
Dim v()
Dim i As Integer
Dim N As Integer
Dim N1 As Integer
' Описание массива X и Y
Dim x(30) As Single
Dim y(30) As Single
' Описание переменных для построения графиков
Dim SngX As Single
bytI As Integer
yy As Single
' SngX - абсцисса точки, y – ордината
' Описание переменных для рассчетных формул
Dim SumX, SumY As Single
Dim Sumx2, SumXY As Single
Dim Sumx3 As Single
Dim Sumx4 As Single
Dim SumX2y As Single
Dim SumLnY As Single
Dim SumXLnY As Single
Dim Xsr As Single
Dim Ysr As Single
Dim SumX_Xsr As Single
Dim SumY_Ysr As Single
Dim Pr_Sum_sr As Single
Dim X_Xsr_2 As Single
Dim Y_Ysr_2 As Single
Dim Sum_ost_lin As Single
Dim Sum_ost_kvad As Single
Dim Sum_ost_exp As Single
Dim koeff_kor As Single
Dim koeff_det_lin As Single
Dim koeff_det_kvad As Single
Dim koeff_det_exp As Single
' Описание переменных и констант для ввода ИД из файла
Dim masXY() As String
Dim inCounter As Integer
Dim inFoundPos As Integer
Dim num As Byte
Const PROBEL = " "
Sub Draw()
' Построение графика функции
' Задание масштаба и новой системы координат
Picture1.Scale (x(0) - 1, y(N) + 20)-(x(N) + 1, y(0) - 20)
For SngX = x(0) - 1 To x(N) + 1 Step 0.005
yy = v(1) + v(2) * SngX ' Вычисление ординаты y
Picture1.PSet (SngX, yy), vbWhite ' Рисуем точку
Next SngX ' Берем следующую абсциссу
' Рисуем ось X
Picture1.Line (x(0) - 1, 0)-(x(N) + 1, 0)
For bytI = x(0) - 1 To x(N) + 1
Picture1.PSet (bytI, 0) ' Рисуем масштаб на оси X
Picture1.Print bytI ' Подписываем масштаб
Next bytI
' Рисуем ось Y
Picture1.Line (0, y(N) + 20)-(0, y(0) - 20)
For bytI = y(0) - 20 To y(N) + 20 Step 20
Picture1.PSet (0, bytI) ' Рисуем масштаб на оси Y
Picture1.Print bytI ' Подписываем масштаб
Next bytI
' Построение точечного графика функции ИД
For i = 1 To N
Picture1.Circle (x(i), y(i)), 0.05, vbBlue
Next i
End Sub
Private Sub Gauss(A(), v(), N As Integer, Epsilon)
' Процедура решения СЛАУ методом Гаусса
Dim Result As Boolean
Dim R(10, 10) As Double
Dim k As Long
Dim u As Long
Dim m As Long
Dim j As Long
Dim i As Long
Dim t As Double
For i = 1 To N
For j = 1 To N + 1
R(i, j) = A(i, j)
Next
Next
u = 0
Result = True
Do
u = u + 1
k = u
Do While Abs(R(k, u)) <= Epsilon And k < N
k = k + 1
Loop
If k <> N Or Abs(R(N, u)) > Epsilon Then
If k <> u Then
m = u
Do
t = R(u, m)
R(u, m) = R(k, m)
R(k, m) = t
m = m + 1
Loop Until Not m <= N + 1
End If
j = N + 1
Do
R(u, j) = R(u, j) / R(u, u)
j = j - 1
Loop Until Not j >= u
m = N + 1
If k + 1 <= N Then
i = k + 1
Do
j = u + 1
Do
R(i, j) = R(i, j) - R(i, u) * R(u, j)
j = j + 1
Loop Until Not j <= m
i = i + 1
Loop Until Not i <= N
End If
Else
Result = False
End If
Loop Until Not (u <> N And Result)
If Result Then
i = N
Do
v(i) = R(i, m)
If i <> 1 Then
k = i - 1
Do
R(k, m) = R(k, m) - R(k, i) * v(i)
k = k - 1
Loop Until Not k >= 1
End If
i = i - 1
Loop Until Not i >= 1
End If
End Sub
Private Sub Command1_Click()
' Считывание исходных данных из текстового файла
num = FreeFile
Open "ID1.txt" For Input As #num
While Not EOF(num)
i = i + 1
ReDim Preserve masXY(i)
Line Input #num, masXY(i)
Wend
Close num
' Заполнение значений массивов X и Y и отображение в ListBox
N = i
For i = 1 To N Step 1
inCounter = 1
inFoundPos = InStr(inCounter, masXY(i), PROBEL)
While inFoundPos <> 0
x(i) = Val(Mid$(masXY(i), inCounter, inFoundPos - inCounter))
inCounter = inFoundPos + 1
inFoundPos = InStr(inCounter, masXY(i), PROBEL)
Wend
If inCounter < Len(masXY(i)) Then
y(i) = Val(Mid$(masXY(i), inCounter))
End If
List1.AddItem x(i)
List2.AddItem y(i)
Next i
' Расчет необходимых величин по формулам
For i = 1 To N Step 1
SumX = SumX + x(i)
SumY = SumY + y(i)
Sumx2 = Sumx2 + x(i) ^ 2
SumXY = SumXY + x(i) * y(i)
Sumx3 = Sumx3 + x(i) ^ 3
Sumx4 = Sumx4 + x(i) ^ 4
SumX2y = SumX2y + x(i) ^ 2 * y(i)
SumLnY = SumLnY + Log(y(i))
SumXLnY = SumXLnY + x(i) * Log(y(i))
Next i
Xsr = SumX / N
Ysr = SumY / N
For i = 1 To N Step 1
SumX_Xsr = SumX_Xsr + (x(i) - Xsr)
SumY_Ysr = Sumy_Xsr + (y(i) - Ysr)
Pr_Sum_sr = Pr_Sum_sr + SumX_Xsr * SumY_Ysr
X_Xsr_2 = X_Xsr_2 + (x(i) - Xsr) ^ 2
Y_Ysr_2 = Y_Ysr_2 + (y(i) - Ysr) ^ 2
Next i
' Линейная аппроксимация
N1 = 2
ReDim A(1 To N, 1 To N + 1)
ReDim B(1 To N)
ReDim v(1 To N)
A(1, 1) = N
A(1, 2) = SumX
A(2, 1) = SumX
A(2, 2) = Sumx2
A(1, 3) = SumY
A(2, 3) = SumXY
Gauss A(), v(), N1, 0.01
Text1.Text = "y = " & Round(v(1), 4) & " + " & Round(v(2), 4) & "x"
For i = 1 To N
Sum_ost_lin = Sum_ost_lin + (v(1) + v(2) * x(i) - y(i)) ^ 2
Next i
koeff_kor = Round(Pr_Sum_sr / Sqr(X_Xsr_2 * Y_Ysr_2), 4)
Text4.Text = koeff_kor
koeff_det_lin = Round(1 - Sum_ost_lin / Y_Ysr_2, 4)
Text5.Text = koeff_det_lin
Draw
' Построение графика функции
For SngX = x(0) - 1 To x(N) + 1 Step 0.005
yy = v(1) + v(2) * SngX ' Вычисление ординаты y
Picture1.PSet (SngX, yy), vbRed ' Рисуем точку
Next SngX ' Берем следующую абсциссу
' Квадратичная аппроксимация
N1 = 3
ReDim A(1 To N, 1 To N + 1)
ReDim B(1 To N)
ReDim B(1 To N)
ReDim v(1 To N)
A(1, 1) = N
A(1, 2) = SumX
A(1, 3) = Sumx2
A(2, 1) = SumX
A(2, 2) = Sumx2
A(2, 3) = Sumx3
A(3, 1) = Sumx2
A(3, 2) = Sumx3
A(3, 3) = Sumx4
A(1, 4) = SumY
A(2, 4) = SumXY
A(3, 4) = SumX2y
Gauss A(), v(), N1, 0.01
Text2.Text = "y = " & Round(v(1), 4) & " + " & Round(v(2), 4) & "x" & " + " & Round(v(3), 4) & "x^2"
For i = 1 To N
Sum_ost_kvad = Sum_ost_kvad + (v(1) + v(2) * x(i) + v(3) * x(i) ^ 2 - y(i)) ^ 2
Next i
koeff_det_kvad = Round(1 - Sum_ost_kvad / Y_Ysr_2, 4)
Text6.Text = koeff_det_kvad
Draw
' Построение графика функции
For SngX = x(0) - 1 To x(N) + 1 Step 0.005
yy = v(1) + v(2) * SngX + v(3) * SngX ^ 2 ' Вычисление ординаты y
Picture1.PSet (SngX, yy), vbGreen ' Рисуем точку
Next SngX ' Берем следующую абсциссу
' Экспоненциальная аппроксимация
N1 = 2
ReDim A(1 To N, 1 To N + 1)
ReDim B(1 To N)
ReDim B(1 To N)
ReDim v(1 To N)
A(1, 1) = N
A(1, 2) = SumX
A(2, 1) = SumX
A(2, 2) = Sumx2
A(1, 3) = SumLnY
A(2, 3) = SumXLnY
Gauss A(), v(), N1, 0.01
Text3.Text = "y = " & Exp(Round(v(1), 4)) & " * " & "exp(" & Round(v(2), 4) & "x)"
For i = 1 To N
Sum_ost_exp = Sum_ost_exp + (Exp(v(1)) * Exp(v(2) * x(i)) - y(i)) ^ 2
Next i
koeff_det_exp = Round(1 - Sum_ost_exp / Y_Ysr_2, 4)
Text7.Text = koeff_det_exp
Draw
' Построение графика функции
For SngX = x(0) - 1 To x(N) + 1 Step 0.005
yy = Exp(v(1)) * Exp(v(2) * SngX) ' Вычисление ординаты y
Picture1.PSet (SngX, yy), vbMagenta ' Рисуем точку
Next SngX ' Берем следующую абсциссу
End Sub
Private Sub Form_Load()
Frame1.Caption = "Исходные данные"
Frame2.Caption = "Линейная аппроксимация"
Frame3.Caption = "Квадратичная аппроксимация"
Frame4.Caption = "Экспоненциальная аппроксимация"
Frame5.Caption = "Графики зависимостей"
Text1.Text = ""
Text2.Text = ""
Text3.Text = ""
Text4.Text = ""
Text5.Text = ""
Text6.Text = ""
Text7.Text = ""
List1.AddItem " X "
List2.AddItem " Y "
Label1.Caption = "КУРСОВАЯ РАБОТА"
Label1.Font.Size = 16
Label1.Alignment = 2
Label2.Caption = "Реализация численного метода с помощью среды программирования Visual Basic 6.0"
Label2.Font.Size = 12
Label2.Alignment = 2
Label3.Caption = "группа СТ-11 студент Максимова Е.Н."
Label3.Font.Size = 12
Label3.Alignment = 2
Label4.Caption = "Коэффициент корреляции"
Label5.Caption = "Коэффициент детерминированности"
Label6.Caption = "Коэффициент детерминированности"
Label7.Caption = "Коэффициент детерминированности"
Command1.Caption = "АППРОКСИМИРОВАТЬ"
End Sub
После нажатия клавиши «АППРОКСИМИРОВАТЬ» форма приняла вид, представленный на рис. 8.
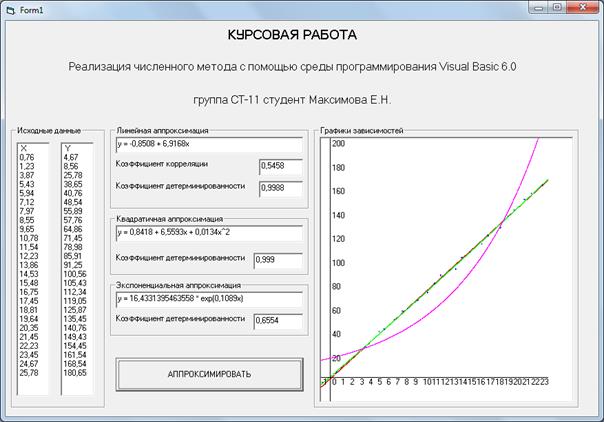
Рис. 8
Заключение
В ходе написания курсовой работы была проведена аппроксимация функции заданной таблично с помощью метода наименьших квадратов. Это было сделано с помощью средств табличного процессора Microsoft Excel и визуальной среды программирования Visual Basic 6.0.
В процессе исследования функция аппроксимировалась линейно, квадратично и экспоненциально, были построены графики зависимостей. По рассчитанным коэффициентам корреляции и детерминированности был сделан вывод о применимости различных полиномов при приближенных вычислениях. Наиболее точный результат дала квадратичная аппроксимация, так как ее коэффициент детерминированности ближе всего к единице.
При сравнении точности результатов, полученных в табличном процессоре Microsoft Excel и в среде программирования Visual Basic 6.0, был сделан вывод о том, что табличный процессор более подходит для решения задач такого рода. Это объясняется тем, что программа Visual Basic 6.0 в отличие от Microsoft Excel проводит вычисления косвенными методами, что сильно влияет на точность получаемых результатов.
Библиографический список
1. Б.П. Демидович, И.А. Марон. Основы вычислительной математики. М.: Государственное издательство физико-математической литературы, 1963.
2. Информатика: Учебник / Под ред. проф. Н.В. Макаровой. М.: Финансы и статистика, 1997.
3. Информатика: Практикум по технологии работы на компьютере/ Под ред. проф. Н.В. Макаровой. М.: Финансы и статистика, 1997.
4. Н. Николь, Р.Альбрехт. Excel 5.0. Электронные таблицы. М.: Изд. “ЭКОМ”, 1996.






