Функция y = f (x) задана таблицей 1:
Таблица 1.
аргумент
| функция
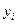
| аргумент
| функция
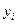
| аргумент
| функция
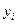
| аргумент
| функция
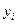
| аргумент
| функция
|
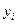
| 0.76 | 4.67 | 7.12 | 48.54 | 11.54 | 79.98 | 16.75 | 112.34 | 21.45 | 149.43 |
| 1.23 | 8.56 | 7.97 | 55.89 | 12.23 | 85.91 | 17.45 | 119.05 | 22.23 | 154.45 |
| 3.84 | 25.78 | 8.55 | 57.76 | 13.86 | 91.25 | 18.81 | 125.87 | 23.45 | 161.54 |
| 5.43 | 38.65 | 9.65 | 64.86 | 14.53 | 100.56 | 19.64 | 135.45 | 24.67 | 168.54 |
| 5.94 | 40.76 | 10.78 | 71.45 | 15.48 | 105.43 | 20.35 | 140.76 | 25.78 | 180.65 |
Требуется выяснить – какая из функций: линейная, квадратичная или экспоненциальная наилучшим образом аппроксимирует функцию заданную таблицей 1.
Решение:
Поскольку в данном примере каждая пара значений (
) встречается один раз, то корреляционная таблица примет вид единичной матрицы. Значит, условные средние значения 
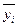совпадают со значениями 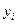. Отсюда следует, что корреляционное отношение 
равно 1 и, следовательно, между y и x существует функциональная зависимость.
Для проведения расчетов мы расположили данные в виде таблицы 2, используя средства табличного процессора Microsoft Excel.
Таблица 2.
Поясним, как составляется таблица 2.
Шаг 1. В ячейки A1:A25 заносим значения .
Шаг 2. В ячейки B1:B25 заносим значения .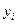
Шаг 3. В ячейку C1 вводим формулу =A1^2.
Шаг 4. В ячейки C2:C25 эта формула копируется.
Шаг 5. В ячейку D1 вводим формулу =A1*B1.
Шаг 6. В ячейки D2:D25 эта формула копируется.
Шаг 7. В ячейку F1 вводим формулу =A1^4.
Шаг 8. В ячейки F2:F25 эта формула копируется.
Шаг 9. В ячейку G1 вводим формулу =A1^2*B1.
Шаг 10. В ячейки G2:G25 эта формула копируется.
Шаг 11. В ячейку H1 вводим формулу =LN(B1).
Шаг 12. В ячейки H2:H25 эта формула копируется.
Шаг 13. В ячейку I1 вводим формулу =A1*LN(B1).
Шаг 14. В ячейки I2:I25 эта формула копируется.
Последующие шаги делаем с помощью автосуммирования.
Шаг 15. В ячейку A26 вводим формулу =СУММ(A1:A25).
Шаг 16. В ячейку B26 вводим формулу =СУММ(B1:B25).
Шаг 17. В ячейку C26 вводим формулу =СУММ(C1:C25).
Шаг 18. В ячейку D26 вводим формулу =СУММ(D1:D25).
Шаг 19. В ячейку E26 вводим формулу =СУММ(E1:E25).
Шаг 20. В ячейку F26 вводим формулу =СУММ(F1:F25).
Шаг 21. В ячейку G26 вводим формулу =СУММ(G1:G25).
Шаг 22. В ячейку H26 вводим формулу =СУММ(H1:H25).
Шаг 23. В ячейку I26 вводим формулу =СУММ(I1:I25).
Аппроксимируем функцию y = f (x) линейной функцией 
. Для определения коэффициентов 
и 
воспользуемся системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 и D26, запишем систему (4) в виде
(11)
решив которую, получим 
и 
.
Таким образом, линейная аппроксимация имеет вид
(12)
Решение системы (11) проводим, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 3.
Таблица 3.
В ячейках A34:B35 записана формула {=МОБР(A30:B31)}.
В E34:E35 записана формула {=МУМНОЖ(A34:B35,C30:C31)}.
Далее аппроксимируем функцию y = f (x) квадратичной функцией 
. Для определения коэффициентов 
воспользуемся системой (5). Используя итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26, D26, E26, F26 и G26 запишем систему (5) в виде
(13)
решив которую, получим 
, 
и 
Таким образом, квадратичная аппроксимация имеет вид
(14)
Решение системы (13) проводили, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 4.
Таблица 4.
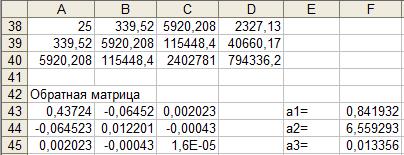
В ячейках A43:C45 записана формула {=МОБР(A38:C40)}.
В F43:F45 записана формула {=МУМНОЖ(A43:C45,D38:D40)}.
Теперь аппроксимируем функцию y = f (x) экспоненциальной функцией 
. Для определения коэффициентов и прологарифмируем значения 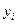и, используя итоговые суммы таблицы 2, расположенные в ячейках A26, C26, H26 и I26 получим систему
(15)
где 
.
Решив систему (10) найдем 
и 
.
После потенцирования получим 
Таким образом, экспоненциальная аппроксимация имеет вид
(16)
Решение системы (15) проводили, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 5.
Таблица 5.
В ячейках A52:B53 записана формула {=МОБР(A48:B49)}.
В E51:E53 записана формула {=МУМНОЖ(A52:B53,C48:C49)}.
В ячейке E53 записана формула =EXP(E51).
Вычислим среднее арифметическое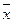 
и 
по формулам:
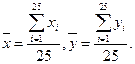
Результаты расчета 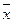и средствами Microsoft Excel представлены в таблице 6.
Таблица 6.
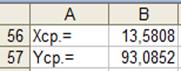
В ячейке B56 записана формула =A26/25.
В ячейке B57 записана формула =B26/25.
Для того чтобы рассчитать коэффициент корреляции и коэффициент детерминированности данные целесообразно расположить в виде таблицы 7, которая является продолжением таблицы 2.
Таблица 7.
Поясним, как таблица 7 составляется.
Ячейки A1:A26 и B1:B26 уже заполнены (см. табл. 2).
Далее делаем следующие шаги.
Шаг 1. В ячейку J1 вводим формулу =(A1-$B$56)*(B1-$B$57).
Шаг 2. В ячейки J2:J25 эта формула копируется.
Шаг 3. В ячейку K1 вводим формулу =(A1-$B$56)^2.
Шаг 4. В ячейки K2:K25 эта формула копируется.
Шаг 5. В ячейку L1 вводим формулу =(B1-$B$57)^2.
Шаг 6. В ячейки L2:L25 эта формула копируется.
Шаг 7. В ячейку M1 вводим формулу =($E$34+$E$35*A1-B1)^2.
Шаг 8. В ячейки M2:M25 эта формула копируется.
Шаг 9. В ячейку N1 ввели формулу =($F$43+$F$44*A1+$F$45*A1^2-B1)^2.
Шаг 10. В ячейки N2:N25 эта формула копируется.
Шаг 11. В ячейку O1 ввели формулу =($E$53*EXP($E$52*A1)-B1)^2.
Шаг 12. В ячейки O2:O25 эта формула копируется.
Последующие шаги делаем с помощью автосуммирования.
Шаг 13. В ячейку J26 вводим формулу =СУММ(J1:J25).
Шаг 14. В ячейку K26 вводим формулу =СУММ(K1:K25).
Шаг 15. В ячейку L26 вводим формулу =СУММ(L1:L25).
Шаг 16. В ячейку M26 вводим формулу =СУММ(M1:M25).
Шаг 17. В ячейку N26 вводим формулу =СУММ(N1:N25).
Шаг 18. В ячейку O26 вводим формулу =СУММ(O1:O25).
Теперь проведем расчеты коэффициента корреляции по формуле (8) (только для линейной аппроксимации) и коэффициента детерминированности по формуле (10). Результаты расчетов средствами Microsoft Excel представлены в таблице 8.
Таблица 8.
В таблице 8 в ячейке B59 записана формула =J26/(K26*L26)^(1/2).
В ячейке B61 записана формула =1- M26/L26.
В ячейке B63 записана формула =1- N26/L26.
В ячейке B65 записана формула =1- O26/L26.
Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные.
