Для выделения постоянной составляющей из сигнала U2 датчика D2 используем фильтр низкой частоты первого порядка, приведенный на рис. 1.6.
Для расчета элементов фильтра необходимо предварительно определить коэффициент пульсаций сигнала U2
q1 = Uм1/Uср,
где Uм1 – амплитуда первой гармоники ряда Фурье; Uср – среднее значение сигнала.
Коэффициент сглаживания
Kc = q1/q2,
где q2 – коэффициент пульсаций на выходе фильтра.
Любой периодический сигнал можно представить в виде ряда гармоник, частоты которых кратны частоте повторения. Амплитуды и фазы этих гармоник будут меняться. Точный характер изменений гармоник зависит от формы сигнала датчика D2. Разложение периодического сигнала на его частотные составляющие выполняется с помощью ряда Фурье. Таким образом, любая периодическая функция может быть представлена следующим образом:

где u(t) – периодическая функция времени;



где ω = 2π/T.
Если сложить синусоидальную и косинусоидальную составляющие гармонического сигнала, то получим следующее уравнение:
A sin ωt + B cos ωt = M sin (ωt + ψ);
 ;
;
ψ = arctg (A/B).
Сигнал u(t) можно представить следующим образом:
u(t) = B0 + M1 sin(ωt + ψ) + … + Mn sin(nωt + ψn) + …
Коэффициенты M1, M2,... Mn являются амплитудами ряда Фурье. Фазовый угол ψn является начальной фазой n-й гармоники при t =0. Любая периодическая функция может четной функцией, или нечетной. Четные функции симметрично относительно начала координат
f(t) = f(-t).
Четная функция не содержит синусоидальных членов. Для четных функций An = 0, ψn = π/2. Четная функция описывается следующим уравнением:
u1(t) = B0 + B1 cos ωt + B2 cos 2ωt +...+ + Bn cos nωt,
где ω = 2πf, f – основная частота.
Нечетные функции несимметричны относительно начала координат
f(-t) = -f(t).
Нечетная функция содержит только синусоидальные члены:
u2(t) = A1 sin ωt + A2 sin 2ωt +... An sin nωt.
В курсовом проекте гармонический анализ сигнала датчика D2 выполнить следующим образом:
- Выбрать один полный период Т заданного сигнала.
- Разделить период на k равных интервалов.
- Определить коэффициенты An при синусоидальных членах в ряду Фурье по уравнению

где An - амплитуда n-й гармоники;
m – номер интервала, равный 1, 2, 3,..., k;
am – амплитуда в m-м интервале периода;
θm – фазовый угол в m-м интервале на частоте 2πm/k [рад].
- Определить коэффициенты Bn при косинусоидальных членах в ряду Фурье по уравнению

Рассмотрим пример разложения в ряд Фурье сигнала, приведенного на рис. 2.20. Сигнал этой формы является четной функцией, поэтому вычисляем только косинусоидальные члены.
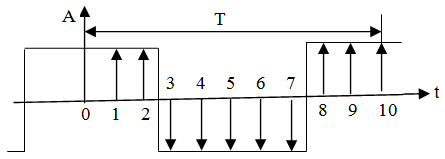
Рис. 2.20. Пример разложения в ряд Фурье сигнала
Для расчета амплитуды первой гармоники ряда Фурье используем табл. 2.3.
Таблица 2.3
| m | am | θm | cos θm | am cos θm | sin θm | am sin θm |
| -1 -1 -1 -1 -1 | 0,809 0,309 -0,309 -0,809 -1,0 -0809 -0,309 0,309 0,809 1,0 | 0,809 0,309 0,309 0,809 1,0 0,809 0,309 0,309 0,809 1,0 ∑=6,472 | 0,588 0,951 0,951 0,588 -0,588 -0,951 -0,951 -0,588 | 0,588 0,951 -0,951 -0,588 0,588 0,951 -0,951 -0,588 ∑=0 |
Амплитуда первой гармоники B1 = 6,472∙2/10 = 1,294.
Для расчета амплитуды второй гармоники ряда Фурье используем табл. 2.4.
Таблица 2.4
| m | am | θm | 2∙θm | cos 2θm | am cos 2θm | sin 2θm | am sin θm |
| -1 -1 -1 | 0,309 -0,809 -0,809 0,309 1,0 | 0,309 -0,809 0,809 0,309 -1,0 | 0,951 0,588 -0,588 -0,951 | 0,951 0,588 0,588 0,951 |
Прод. таблицы 2.4
| m | am | θm | 2∙θm | cos 2θm | am cos 2θm | sin 2θm | sin 2θm |
| -1 -1 | 0,309 -0,809 -0,809 0,309 1,0 | -0,309 0,809 -0,809 0,309 1,0 ∑ = 0 | 0,951 0,588 -0,588 -0,951 | -0,951 -0,588 -0,588 -0,951 ∑ = 0 |
Амплитуда второй гармоники B2 = 0.
Определим среднее значение сигнала, показанного на рис. 2.21.
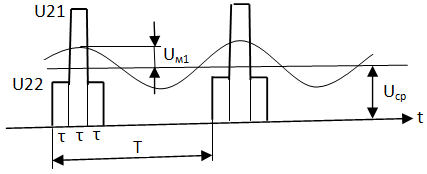
Рис. 2.21. Пример определения среднего значения
Среднее значение Uср = (A21∙τ + 2∙A22∙τ) / T.
Рассчитать фильтр низкой частоты первого порядка, приведенный на рис. 1.6, если коэффициент пульсаций на входе фильтра q1 = 1,57, а на выходе фильтра q2 = 0,01. Частота первой гармоники f1 = 5000 Гц. Коэффициент усиления фильтра K = 2.
Решение.
Пусть R0 = 24 кОм;
R = R0 / K = 12 кОм;
KдБ = 20∙lg 2 = 6 дБ;
Kc = q1 / q2 = 1,57 / 0,01 = 157;
Kс дБ 20∙lg 157 = 43,9;
На графике в логарифмическом масштабе (рис. 2.22) проводим две прямые линии на уровне
KдБ = 6 дБ и KдБ1 = KдБ - Kс дБ = 6 – 43 = -37,9 дБ.
Из точки, координаты которой (KдБ1, f1), проводим прямую линию с наклоном в 20 дБ/дек до пересечения с прямой на уровне KдБ = 6 дБ. Точка пересечения дает значение частоты среза fср = 30 Гц. Шкала частоты в пределах одной декады показана на рис. 2.23.

Рис. 2.22. Построение частотной характеристики фильтра

Рис. 2.23. Шкала частоты в пределах одной декады
По полученной частоте среза fср и величине резистора R определяем емкость конденсатора
C = 1 / 2∙π∙fср∙R0 = 1,3∙10-9 Ф
Программа определения параметров фильтра (рис. 1.2):
u21=16; u22=8; u23=2; f1=110; f2=11;
n=2*f1/f2;
d=360/n;
gm=d:d:360;
for m=1:n
am(m)=-u23;
u23=-u23;
end
am1=am;
am1(1)=u22; am1(2)=u21;
am2=am1;
rm=gm.*pi/180;
cm=cos(rm);
sm=sin(rm);
acm=am2.*cm;
asm=am2.*sm;
cms=sum(acm.');
sms=sum(asm.');
b1=2*cms/n;
a1=2*sms/n;
ab2=b1^2+a1^2;
um1=sqrt(ab2)%амплитуда 1-й гармоники
ss=sum(am2.');
sss=ss/n %среднее значение
Kp=um1/sss %коэффициент пульсаций
F1=f2 %частота 1-й гармоники
Kc=Kp/0.01 %коэффициент сглаживания
Kcdb=20*log10(Kc)
K=0.9/sss %коэффициент усиления
Kdb=20*log10(K) %коэффициент усиления в дБ
Kdb1=Kdb-Kcdb
%построение графика к п.2 курсового проекта
x=logspace(-1,3);%диапазон частот графика
a=abs(x)-abs(x);
aa=a+20;%верхняя граница графика
bb=a-60;%нижнияя граница графика
semilogx(x,aa,x,bb,x,Kdb,'.r',x,Kdb1,'.r')
grid
xlabel('Frequency, Hz')
ylabel('Db')
fk=F1/1000;%регулировка линии наклона
Kdb2=Kdb1+60;
hold on
line([fk F1],[Kdb2 Kdb1],'color','red')%линия наклона -20 dB/dec
line([1 100],[0 -40],'color','blue')%тестовая линия накл.
hold off
figure
stem(am2,'k'),grid
Расчетные параметры фильтра
um1 = 2.3713 sss = 1.2000 Kp = 1.9761
F1 = 11
Kc = 197.6065 Kcdb = 45.9160 K = 0.7500
Kdb = –2.4988 Kdb1 = –48.4148
На рис. 2.24 показана импульсная характеристика входного сигнала фильтра, а на рис. 2.25 – амплитудно-частотная характеристика (АЧХ) этого фильтра (вариант 1).
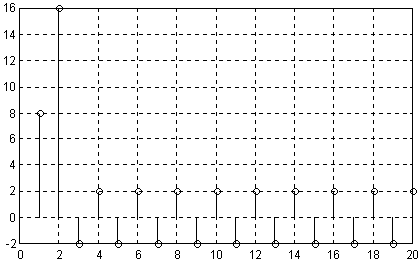
Рис. 2.24. Импульсная характеристика входного сигнала фильтра

Рис. 2.25. АЧХ фильтра (вариант 1)
Результат расчета резистора R, конденсатора C и частотной характеристики фильтра низкой частоты первого порядка проверяем с помощью схемы, приведенной на рис. 2.26.
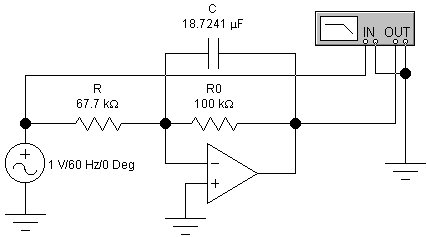
Рис. 2.26. Фильтр низкой частоты первого порядка
Из частотной характеристики фильтра (рис. 2.27) видно, что на частоте 16.51 Гц затухание составляет –42.36 дБ. По расчетным данным затухание сигнала на частоте f2 равно Kdb1 = –42.3927 дБ. С помощью маркера определяем величину коэффициента Kdb на частоте меньше частоты среза.

Рис. 2.27. Частотная характеристика фильтра
Величину постоянного напряжения U4 и коэффициент пульсаций на выходе фильтра проверяем с помощью последовательного соединения датчика D2 и фильтра низкой частоты. Пульсацию напряжения U4 определить в установившемся режиме.

Рис. 2.32. Схема определения напряжения и коэффициента пульсаций на выходе фильтра
По осциллограмме сигнала U4 (рис. 2.33) определяем абсолютную пульсацию, которая равна 55,604 мВ. Относительная пульсация сигнала q2 = 55,604/1190 = 0,0467 (4,67%).

Рис. 2.33. Осциллограммы сигнала U2i на выходе датчика D2
и сигнала U4 на выходе фильтра низкой частоты
При необходимости параметры фильтра можно скорректировать.
Расчет сумматора
Схема сумматора приведена на рис. 1.7. Для АЦП рис. 1.8, 1.9 напряжение на выходе сумматора U5 =10 В, а для АЦП рис. 1.10 напряжение U5 = 2 В. Для расчета цепи смещения R3, R4, R5 и R6 используем метод узловых напряжений:

где Ek – напряжение участка цепи, Gk – проводимость участка цепи.
Программа расчета резистора R6 и величины –Ua:
%Задаваемые параметры
%Величина резистора R3=0 - 200 Ом
E1=12; E2=-12;
Ua=0.02;%Соответствует номеру варианта
R5=1e3; R4=0.9e3;
R3=0;
%Расчет резистора R6
R34=R4+R3;
g34=1/R34;
g5=1/R5;
g6=((E1*g34+E2*g5)/Ua)-g34-g5;
R6=1/g6
%Расчет -Ua
R3=200;
R34=R4+R3;
g34=1/R34;
Ua=(E1*g34+E2*g5)/(g34+g5+g6)
Результат расчета: R6 = 15.4905, Ua = –0.0164.
Отрицательное значение Ua меньше расчетного, поэтому увеличиваем R6 до 20 Ом.
Программа построения зависимости Ua = f(R6):
R6=15.49;%Расчетное значение
E1=12; E2=-12;
R5=1e3; R4=0.9e3;
R3=1:200;%Диапазон изменения резистора R3
%Расчет
R34=R4+R3;
g34=1./R34;
g5=1/R5; g6=1/R6;
Ua=(E1.*g34+E2.*g5)./(g34+g5+g6);
R6=20;%Измененное значение
g6=1/R6;
Ua1=(E1.*g34+E2.*g5)./(g34+g5+g6);
plot(R3,Ua,':K',R3,Ua1,'K')
grid
xlabel('R6=15.49 – пунктирная линия; R6=20 - сплошная линия')
ylabel('Ua')
Результат расчета: R6 = 15.4905, Ua = –0.0164.
На рис. 2.34 показано семейство характеристик Ua = f(R6) при различных значениях R6.

Рис. 2.34. Семейство характеристик Ua = f(R6)
Проверяем правильность расчета напряжения смещения Ua. Собираем схему, показанную на рис. 2.35 и устанавливаем R3 = 0 (движок потенциометра находится в крайнем левом положении). Напряжение Ua соответствует расчетному значению, а напряжение U5 = 3·Ua.

Рис. 2.35. Проверка цепи смещения сумматора при R3 = 0
На рис. 2.36 рассмотрен случай проверки смещения, когда R3 = 200 Ом.
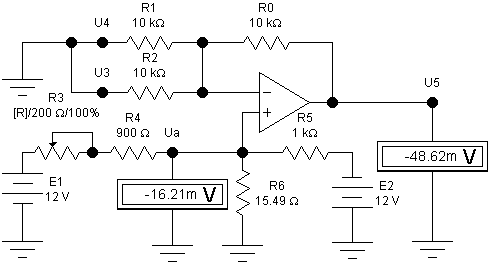
Рис. 2.36. Проверка цепи смещения сумматора при R3 = 200 Ом
Напряжение Ua соответствует расчетному значению.






