В отличие от сеточных методов Годунова, в GSPH все взаимодействия между частицами i и j ограничиваются до одномерной задачи на линии, соединяющей две взаимодействующие частицы, даже в трехмерных задачах. Таким образом, одномерное решение задачи Римана достаточно даже для многомерного кода SPH-Годунова.
В этом заключается преимущество GSPH по сравнению с сеточными методами Годунова, поскольку эффективного решения задачи Римана для случая многомерной задачи не существует. (Monaghan 1997). Метод декомпозиции оператора является ключевым в сеточных методах Годунова для описания многомерной задачи одномерной задачей Римана, но в GSPH никакой геометрической декомпозиции не требуется.
На рисунке 6 показано развитие НКГ в диагональном направлении. Перепад плотности составляет 1:2, и все начальные условия являются такими же, как в предыдущем моделировании, приведенном в разделе 4.1, за исключением начального распределения частиц. Начальное распределение частиц повернуто на 45°. Видны хорошо развитые вихри по диагонали рисунка.
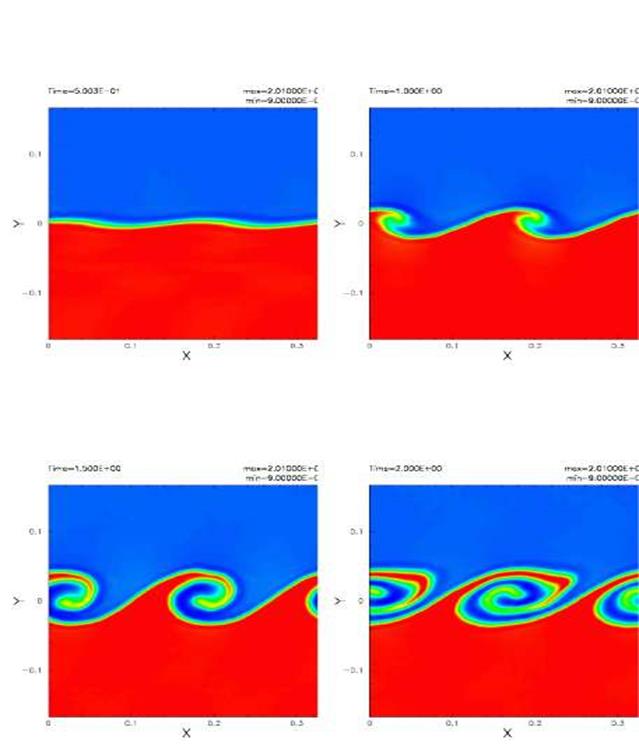
Рисунок 3. Моделирование НКГ в двух слоях различной плотности. Первоначальный перепад плотностей слоев составляет 1:2, а первоначальные числа Маха верхнего и нижнего слоев составляют 0.22 и 0.3 соответственно. Верхний слой движется вправо, а нижний слой движется влево. Первоначальный контактный разрыв между двумя слоями начинает извиваться вследствие первоначального возмущения, а затем вокруг разрыва развиваются хорошо закрученные вихри. Время каждого снимка нормализовано в единицах τкг и показано в верхнем левом углу каждого кадра.
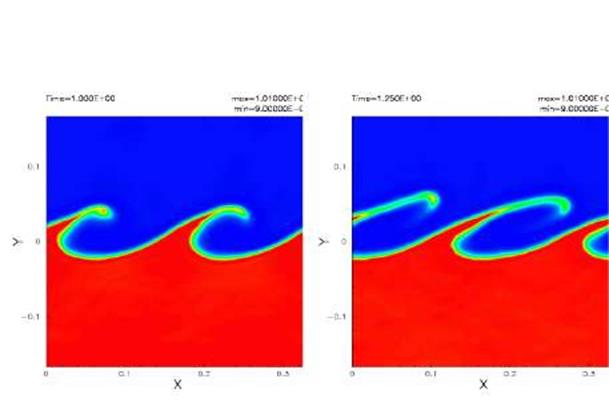
Рисунок 4.Распределение давления в тесте, приведенном на рисунке 3, при t = 1.0 and 2.0τкг – Данные карты распределения давления показывают, что помех значительно меньше, чем в стандартном SPH-методе, (см. рис. 6 в Price (2008)). Заметим, что Price (2008) получил аналогичные результаты с членом искусственной теплопроводности.
|
Тест с пузырем
Взаимодействие между плотным пузырем и сильной ударной волной – весьма интересный вопрос в контексте образования и развития звезд и галактик (Murray и др., 1993; Klein и др., 1994; Jones и др., 1996; Vietri и др., 1997). Если плотный пузырь столкнулся с ударной волной (например, звездный ветер или остаток вспышки сверхновой звезды), то он будет сжиматься и в конечном итоге разрушается. Разрушение плотного пузыря начинается за счет неустойчивостей Тейлора-Реле и Рихтмайера-Мешкова (Inogamov 1999), а затем усиливается за счет НКГ. Однако в стандартном SPH-методе неустойчивости или комбинация неустойчивостей практически не случаются по причине наличия нефизической силы впереди сжатого пузыря, поэтому пузырь в течение долгого времени сохраняется в сжатом состоянии в горячей окружающей среде (A07).
Мы провели тест с пузырем по коду GSPH. Расчетной областью теста с пузырем является [- 2, 30] x [- 6, 6]. Сначала плотный пузырь находится в начале координат и окружен горячей средой, движущейся в направлении х. Радиус пузыря равен 1, а отношение плотностей среды и пузыря χ определено равным 10. Начальное число Маха окружающей среды 5. Количество частиц, задействованных в пузыре и в окружающей среде, составляет 7688 и 93139 соответственно. Начальная конфигурация распределения частиц – стекло (A07). Скорость звука и плотность окружающей среды равны 1. При таких начальных условиях время разрушения облака (Klein и др., 1994), τcc определяется как
(26)
где rb, и va – радиус пузыря и скорость окружающей среды соответственно. Jones и др., (1996) определили «время разрушения пули», но единственной разницей между τcc и временем разрушения пули является численный коэффициент (= 2), поэтому мы использовали τcc в качестве единицы времени в тесте с пузырем. В конечном итоге масштаб времени НКГ (A07) в тесте с пузырем определяется как
(27)
|
Рисунок 5. Моделирование НКГсо значительно более существенным перепадом плотностей. Нижний слой в 10 раз плотнее верхнего слоя. В области разрыва образуются вихри, которые затем вытягиваются и эволюционируют в течение долгого времени. Такое вытягивание может являться результатом низкого разрешения верхнего слоя.
τcc в данном тесте с пузырем составляет 0.63.
На рисунке 7 представлены результаты теста. На ранней стадии взаимодействия происходит сжатие. Передняя часть пузыря сжимается за счет лобового давления окружающей среды. Сзади пузырь испаряется. Вокруг сжатого пузыря образуется головная ударная волна, и в результате неустойчивостей Релея-Тейлора и Рихтмайера-Мешкова образуется три пальцевидных профиля. Эти пальцевидные профили усиливаются НКГ, что приводит к образованию грибовидного профиля на концах пальцевидных профилей. (например, Yabe и др., 1991). Результаты теста пузыря, выполненного по коду GSPH, аналогичны результатам, полученным при помощи сеточного кода (например, Klein и др., 1994).
Выводы
Стандартный SPH-метод не точно описывает градиент давления в месте большого градиента плотности, поэтому в таких случаях не способен описать НКГ. Это происходит вследствие неточного расчета силы, действующей поперек градиенту плотности. Поперек градиенту плотности действует нефизическая сила, которая отталкивает частицы от начального разрыва, что создает щель и гасит начальное возмущение. Таким образом, развитие любой неустойчивости на градиенте плотности подавляется.
Неточный расчет силы происходит вследствие несогласованности стандартного SPH-метода. При аппроксимации частиц, используемой при выводе уравнения движения в стандартном SPH-методе, теряется согласованность нулевого порядка, если частицы распределены неравномерно. Для вывода уравнения импульса можно воспользоваться функцией Лагранжа, но в стандартном SPH-методе функция Лагранжа уже использует аппроксимацию частиц, поэтому в итоговом уравнении импульса по-прежнему будет присутствовать нефизическая сила, действующая поперек градиенту плотности.
Для того чтобы решить проблему согласованности стандартного SPH-метода, мы использовали новую формулировку I02, именуемую GSPH. Новое уравнение импульса было получено с помощью свертки ядра. Мы доказали, что уравнение импульса в методе GSPH имеет линейную согласованность до точности, при которой можно вычислить интеграл свертки ядра, что приводит к существенному снижению действия нефизической силы поперек градиенту плотности при равновесном давлении. То же уравнение импульса можно получить, используя новую функцию Лагранжа (I02). Оно очень похоже на функцию Лагранжа, используемую в стандартном SPH-методе, но оно более близко к функции Лагранжа для реальной жидкости.
Мы объяснили геометрическое значение уравнения движения в методе GSPH. Оно рассматривает основные и соседние частицы как растянутое тело и использует подробную информацию о растянутых тел. В стандартном SPH-методе основные частицы сглаживаются за счет вклада соседей, но эти соседи считаются точкой.
Для демонстрации работы GSPH были проведены расчеты тестовых задач двух типов. Один тест – это традиционный тест НКГ в двух слоях,
|
Рисунок 6. НКГ, развивающаяся в диагональном направлении. Это, по существу, тот же тест, что приведен на рисунке 3, но начальное распределение частиц повернуто на 45°. В отличие от сеточных методов Годунова, GSPH может описать многомерную задачу одномерным решением задачи Римана, поэтому не требуется декомпозиции оператора.
а другой – это тест с пузырем (каплей). В тесте с двумя слоями GSPH показал развитие НКГ даже при очень большом перепаде плотностей. Была проверена также НКГ, развивающаяся по диагонали, и получены удовлетворительные результаты. В тесте с пузырем по коду GSPH можно описать образование и развитие пальцевидных профилей на передней части сжатого пузыря вследствие неустойчивостей и комбинаций неустойчивостей. Результаты теста с пузырем по коду GSPH совпадают с результатами сеточных кодов.
В стандартном SPH-методе при неравномерном распределении частиц не согласуется не только уравнение импульса, но и уравнение сохранения энергии. Мы изучаем влияние несогласованности на уравнение сохранения энергии, и это тема нашей следующей работы.
|
Рисунок 7. Результаты теста с пузырем. Каждый снимок сделан при t = 1, 3, 4, 5, 6 и 7 τcc, начиная с верхнего левого угла, и показывает различные стадии развития пузыря внутри горячей движущейся окружающей среды. Мы взяли квадратный корень от столбцовой плотности для получения цветной карты плотности поверхности. На начальной стадии пузырь сжимается за счет лобового давления окружающей среды. В передней части сжатого пузыря можно увидеть головной скачок уплотнения. Окружающая среда, входя в головную ударную волну, замедляет движение, а затем инициируются неустойчивости Релея-Тейлора и Рихтмайера-Мешкова. Три пальцевидных профиля начинают образовываться в передней части пузыря (третий снимок), а затем эти пальцевидные профили усиливаются за счет неустойчивостей. На кончиках «пальцев» образуются грибовидные профили. Эти результаты хорошо совпадают с результатами сеточных кодов. Заметим, что это двумерное моделирование, в то время как тест пузыря в A07 был выполнен в трехмерном исполнении.
REFERENCES
Agertz O., Moore B., Stadel J., Potter D., Miniati F., Read J., Mayer L., Gawryszczak A., Kravtsov A., Nordlund Å., Pearce F., Quilis V., Rudd D., Springel V., Stone J., Tasker E., Teyssier R., Wadsley J., Walder R., 2007, MN-RAS, 380, 963
Balsara D. S., 1995, J. Comp. Phys., 121, 357
Barnes J., Hut P., 1986, Nature, 324, 446
Bryan G. L., Norman M. L., 1997, in Clarke D. A., West M. J., eds, Computational Astrophysics; 12th Kingston Meeting on Theoretical Astrophysics Vol. 123 of Astronomical Society of the Pacific Conference Series, Simulating X-Ray Clusters with Adaptive Mesh Refinement. pp 363-368
Cha S.-H., Whitworth A. P., 2003a, MNRAS, 340, 73
Cha S.-H., Whitworth A. P., 2003b, MNRAS, 340, 91
Courant R., Friedrichs K. O., 1948, Supersonic flow and shock waves. Interscience, New York
Despres B., 2003, Mathematics of Computation, 73, 1203
Dilts G. A., 1999, International Journal for Numerical Methods in Engineering, 44, 1115
Fryxell B., Olson K., Ricker P., Timmes F. X., Zingale M., Lamb D. Q., MacNeice P., Rosner R., Truran J. W., Tufo H., 2000, ApJS, 131, 273
Fulk D. A., 1994, PhD thesis, Air Force Institute of Technology
Gary J., 1966, SIAM J. Numer. Anal., 3, 467
Gingold R. A., Monaghan J. J., 1977, MNRAS, 181, 375
Inogamov N. A., 1999, Astrophysics and Space Physics Reviews, 10, 1
Inutsuka S.-I., 2002, J. Comp. Phys., 179, 238
Jones T. W., Ryu D., Tregillis I. L., 1996, ApJ, 473, 365
Klein R. I., McKee C. F., Corella P., 1994, ApJ, 420, 213
Kravtsov A. V., Klypin A. A., Khokhlov A. M., 1997, ApJS, 111, 73
LeVeque R. J., 2002, Finite Volume Mothods for Hyperbolic Problems. Cambridge University Press, Cambridge
Liu M. B., Liu G. R., 2006, Appl. Numer. Math., 56, 19
Liu M. B., Liu G. R., Lamb K. Y., 2003, J. Comp. Appl. Math., 155, 263
Lucy L. B., 1977, AJ, 82, 1013
Miniati F., Corella P., 2007, J. Comp. Phys., 227, 400
Monaghan J. J., 1982, SIAM J. Sci. and Stat. Comp., 3, 422
Monaghan J. J., 1987, SPH Meets the Shocks of Noh, Monash University Preprint
Monaghan J. J., 1989, J. Comp. Phys., 82, 1
Monaghan J. J., 1992, ARA&A, 30, 543
Monaghan J. J., 1997, J. Comp. Phys., 136, 298
Morris J. P., 1996, PASA, 13, 97
Murray S. D., White S. D. M., Blondin J. M., Lin D. N. C., 1993, ApJ, 407, 588
Price D. J., 2008, J. Comp. Phys., 227, 10040
Price D. J., Monaghan J. J., 2004, MNRAS, 348, 139
Ritchmyer R. D., Morton K. W., 1967, Difference Methods for Initial-Value Problems, 2nd edn. No. 4 in Interscience Tracts in Pure and Applied Mathematics, John and Wiley & Sons, New York
Springel V., Yoshida N., White S. D. M., 2002, New Astronomy, 6, 79
Stone J. M., Norman M. L., 1992, ApJS, 80, 753
Swegle J. W., Hicks D. L., Attaway S. W., 1995, J. Comp. Phys., 116,123
van Leer B., 1997, J. Comp. Phys., 135, 229
Vietri M., Ferrara A., Miniati F., 1997, ApJ, 483, 262
Wadsley J. W., Stadel J., Quinn T., 2004, New Astronomy, 9, 137
Watkins S. J., Bhattal A. S., Francis N., Turner J. A., Whitworth A. P., 1996, A&AS, 119, 177
Yabe T., Hoshino H., Tsuchiya T., 1991, Phys. Rev. A, 44, 2756
[1] НКГ можно инициировать и по схеме 1-го порядка, но она не очень хорошо развивается. Детали реализации GSPH 2-го порядка очень похожи на схему MUSCL (van Leer, 1997), и здесь не приводятся, поскольку описаны в I02
