Вероятно, наиболее важной характеристикой математической модели является сходимость, поскольку именно она определяет, насколько приближена математическая модель к фактическому (реальному) решению. Однако в общем случае прямо подтвердить сходимость математической модели нелегко, поскольку в большинстве задач фактического решения нет. Поэтому для проверки сходимости математической модели весьма полезно воспользоваться теоремой эквивалентности Лакса (или Лакса-Рихтмайера) (например, Gary, 1966, Ritchmyer и Morton, 1967; Despres, 2003). Согласно теореме эквивалентности Лакса устойчивость и согласованность являются достаточными условиями сходимости.
Во-первых, устойчивость можно четко определить, и она до настоящего времени интенсивно изучалась в стандартном SPH-методе (Monaghan, 1989; Balsara, 1995; Swegle и др., 1995; Morris, 1996; Cha и Whitworth, 2003a), по крайней мере, для линейных алгоритмов. Стандартный SPH-метод условно устойчив, и при условии Куранта-Фридриха-Леви (Courant & Friedrichs, 1948) устойчивость стандартного SPH-метода гарантирована.
Во-вторых, согласованность математической модели означает, насколько хорошо числовые уравнения модели аппроксимируют физические уравнения (Fulk, 1994; LeVeque, 2002), и непосредственно связана с анализом ошибки округления (аппроксимации). Если модель согласована, то ошибка аппроксимации математической модели должна исчезнуть по мере того, как временной шаг, Δt, и размер сетки, Δx (а в SPH-методе – длина сглаживания, h, аналогичная Δx в сеточных кодах), приближаются к бесконечно малому значению. Таким образом, отсутствие согласованности приведет к неточности математической модели. Можно сконцентрироваться на согласованности, чтобы добиться сходимости, поскольку устойчивость уже доказана.
Поскольку проблема согласованности стандартного SPH-метода хорошо известна (см., например, Fulk, 1994; Dilts, 1999), то она будет лишь кратко затронута в следующих разделах для удобства читателей. Для получения уравнения импульса стандартного SPH-метода необходимо сделать две аппроксимации. Первая – это ядерная аппроксимация, и вторая – аппроксимация частиц. Согласованность стандартного SPH-метода будет проверена для обеих аппроксимаций.
Ядерная аппроксимация
Ядерная аппроксимация выражается следующей формулой:
(1)
где W и <f> – ядро и сглаженные по ядру функции соответственно.
Чтобы проверить порядок согласованности ядерной аппроксимации, мы будем следовать методике Liu & Liu (2006). Если численная схема приводит к многочлену до точно определенного n-го порядка, то о такой схеме говорят, что она имеет аппроксимацию n-го порядка. Например, чтобы проверить согласованность нулевого порядка для ядерной аппроксимации, следует подставить функцию f (x’) = C0 в уравнение (1), и тогда сглаженная ядром функция примет вид:
(2)
При этом используется следующее условие нормировки ядерной функции:
(3)
Из уравнения (2) легко выводится аппроксимация нулевого порядка. Для согласованности 1-го порядка следует вставить линейную функцию С0 + С1х’ в f (x’), и тогда
(4)
В данном случае используются условие нормировки (уравнение 3) и свойство симметрии ядерной функции
(5)
Для более высокого порядка согласованности нам нужен более высокий момент ядерной функции. Например, для согласованности 2-го порядка нужно, чтобы 2-ой момент ядерной функции был
(6)
Однако добиться этого, используя неотрицательную ядерную функцию, невозможно. Таким образом, согласованность ядерной аппроксимации при неотрицательной и нормализованной симметричной ядерной функции составляет менее 2.
Для более полного рассмотрения мы можем повторить вышеприведенные действия и для первой производной f (x), поскольку уравнения гидродинамики содержат первую производную физических величин. Однако необходимо проверять не только согласованность, поэтому такой анализ здесь не приводится. Для более подробной информации см. Monaghan (1982) или Liu et al. (2003).
Согласованность зависит от условия нормировки ядра. Таким образом, ядерная аппроксимация теряет свой нулевой порядок согласованности, если условие нормировки не удовлетворено, например, на краю плотного облака в разреженной окружающей среде. Однако численные эксперименты, представленные в A07 и в разделе 4, имеют корректные реализации граничных условий, поэтому несовершенство ядерной функции на границе не является критической проблемой для тестов.
И хотя ядерная аппроксимация имеет согласованность, она не используется напрямую в уравнениях SPH. Вместо ядерной аппроксимации для вывода стандартных уравнений SPH используется аппроксимация частиц, объяснение которой представлено ниже.
Аппроксимация частиц
Аппроксимация частиц, используемая в стандартном SPH-методе, выражается формулой
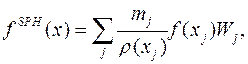(7)
где Wj – это W(x – xj, h).
Мы повторим ту же процедуру, которая была использована в предыдущем разделе, для проверки согласованности аппроксимации частиц. Для случая нулевого порядка подставим константу Co вместо f (xj) в уравнение. (7), тогда
(8)
Аппроксимация частиц может воспроизвести постоянную функцию, когда
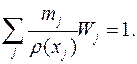(9)
Уравнение (9) имеет место только при равномерном распределении частиц. Поэтому аппроксимация частиц теряет нулевой порядок согласованности при неравномерном распределении частиц, и в конечном счете стандартный SPH-метод не может сойтись к фактическому решению в данной ситуации.
Эта проблема появляется в уравнении движения стандартного SPH-метода. При равновесном давлении одно из типичных уравнений движения стандартного SPH-метода, без учета искусственной вязкости, можно написать следующим образом:
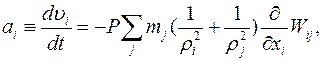(10)
где Wij – это W(xi – xj, h), а физические переменные имеют свои обычные обозначения. Хотя предполагается равновесное давление, гидродинамическое ускорение частицы i не исчезнет, и она будет двигаться. На рисунке 1 представлена эта нефизическая сила. Расчетное ускорение (сплошная красная линия с точками) должно исчезнуть, поскольку давление постоянно поперек разрыва плотности. Однако ускорение приводит к расталкиванию частиц на разрыве. Это расталкивание гасит первоначальное возмущение и подавляет НКГ. Оно также создает щель между двумя слоями разной плотности. Таким образом, понятно, что возникновение нефизической силы по градиенту плотности при равновесном давлении происходит вследствие потери согласованности нулевого порядка.
Единственный путь устранения этой нефизической силы – сделать член с плотностью в круглых скобках уравнения (10) четной функцией. В частности, интерес представляет поле равномерной плотности вокруг частицы i, что является причиной того, что в случае однородной плотности (контраст плотности 1:1) появляется НКГ в A07. Однако равномерное распределение частиц – это особая ситуация, а не общий случай.
СОГЛАСОВАННОСТЬ GSPH
Свертка ядра
Несогласованность стандартного SPH-метода происходит из-за уравнения (9), которое появляется при переходе от континуума (ядерная аппроксимация) к системе частиц (аппроксимация частиц). I02 и Dilts (1999) указали на уравнение (9) как на грубое допущение, и в I02 предложено оценивать плотность в произвольной точке х по формуле
(11)
Из уравнения (11) получаются два тождества:
(12)
и
. (13)
Рисунок 1. Черная и синяя сплошные линии – профили плотности и давления соответственно. Точки на линиях обозначают положения частиц. Они определяют градиент плотности при равновесном давлении. Расстояние частицы от центра, х, рассчитывается по длине сглаживания, h. Красная сплошная линия с точками – ускорение частиц, рассчитанное по стандартному SPH-методу. Красная сплошная линия без точек показывает прогнозируемое ускорение при равновесном давлении. Расталкивание происходит на разрыве плотности и гасит начальное возмущение. Таким образом, в стандартном SPH-методе любая неустойчивость по градиенту плотности может быть подавлена.
Вместо уравнения (9) в ядерную аппроксимацию (уравнение (1)) было вставлено уравнение (12), чтобы избежать несогласованности аппроксимации частиц. Таким образом, окончательная форма аппроксимации ядра в методе GSPH имеет вид:
(14)
Смысл уравнения (14) понятен. Метод GSPH рассматривает как частицы-призраки, так и соседние частицы, как протяженные частицы и использует информацию о подробной внутренней структуре двух протяженных частиц. Заметим, что стандартный SPH-метод рассматривает частицу-призрак как сглаженную частицу вкладом ее соседей, но соседние частицы так и остаются точкой. fGSPH (x)вуравнении (14) сводится к аппроксимированной функции частиц, если частица j рассматривается как точка. Если W(x’ – xJ, h) уравнения (14) аппроксимировано дельта-функцией, δ (x' – xJ), то уравнение (14) примет вид:
(15)
что идентично уравнению (7), если его рассматривать при x = xi.
Для проверки согласованности GSPH вставим линейную функцию С0 + С1x’ в f(x) правой части уравнения (14), тогда
(16)
где использованы уравнения (3), (5) и (12). Уравнение (14) может дать линейную функцию, таким образом, первый порядок согласованности в SPH-методе Годунова гарантирован.
И, наконец, выводим уравнение для импульса, используя уравнения (11) - (14):
(17)
где Wi, ði и ði-это W(x — xi,h), 
соответственно. В отличие от уравнения импульса в стандартном SPH-методе, уравнение (17) должно привести к реальному решению, даже при большом градиенте плотности. Чтобы проверить это, мы исследуем поведение уравнения (17) при общем поле плотности и равновесном давлении:
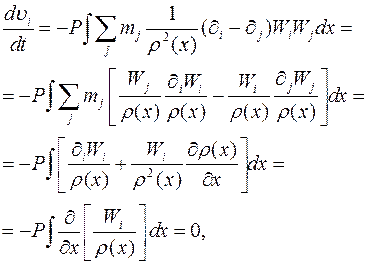(18)
где использованы уравнения (12) и (13). Можно увидеть, что ускорение, вычисленное по уравнению (17), исчезает при равновесном давлении, независимо от поля плотности, до значения, при котором интерполяция поля плотности, используемая для расчета интеграла в GSPH (см. I02), является точной.
