Модулем комплексного числа называют выражение 
Аргумент комплексного числа это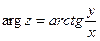 
. Аргумент 
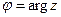изменяется в диапазоне 
и рассчитывается по формуле
| x | y | четверть | аргумент |
| + | + | 
| |
| + | - | 
| |
| - | + | 
| |
| - | - | 
| |
| + | 
| ||
| - | 
|
Пример. Найти модуль и аргумент числа z=1-i.
X=1, y=-1, 
то 
, 
т.к. число z=1-i лежит в четвертой четверти.
Запись комплексного числа в виде z= 
называют тригонометрической формой комплексного числа, где 
Пример. Записать тригонометрическую форму числа z=1-i.
Z= 
Тригонометрическая форма используется для возведения комплексных чисел в степень и извлечения корня.
Возведение комплексного числа в степень осуществляется с помощью формулы Муавра
Примеры. а) Вычислить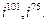 
Учитывая, что 
запишем показатель степени в виде суммы двух слагаемых одно из которых кратно четырем:
в) Вычислить (-1+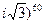 
.
Решение. Представим число 
в тригонометрической форме
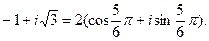
Применяя формулу Муавра, получим
Извлечение корня из комплексного числа осуществляется с помощью формулы
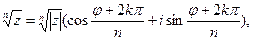
Где к=0,1,2,…..,n-1,
Корень n-й степени из комплексного числа z имеет n различных значений.
Пример. Найти все значения 
Приводим число (
) к тригонометрическому виду
1-i=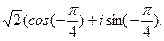 
Следовательно, 
Полагая k=0,1,2,3,найдем
(k=0) 
(k=1) 
(k=2) 
(k=3) 
Показательная форма комплексного числа
По формуле Эйлера 
, то z= 
Это показательная форма комплексного числа.
Пример. Записать число 
в показательной форме.
Найдем модуль и аргумент числа: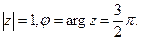 
Показательная форма 
Упражнения. 1.Найти модуль и аргумент комплексного числа 
2. Вычислить 
где 
3.Записать тригонометрическую и показательную форму числа 
Домашняя работа: выполнить вариант домашней контрольной работы по разделу комплексные числа.
Раздел 1. Комплексные числа.
ЗАДАЧА 1. Даны комплексные числа z1, z2 и z3. Необходимо
А) найти число 
Б) изобразить на комплексной плоскости данные комплексные числа, найти их модули и аргументы;
В) записать комплексные числа z1, z2 и z3 в тригонометрической и показательной формах.
Данные к условию задачи, соответствующие вариантам:
Задача 2. Найти все корни уравнений.
Данные к условию задачи, соответствующие вариантам:
1) а) z4+1=0, b) 2z2+3z+5=0 11) a) z4-1=0, b) z2+z+5=0 21) a) z5-1-i=0, b) z2+z+9=0
2) a) z3-1=0, b) z2+2z+5=0 12) a) z3+1=0, b) 2z2-z+3=0 22) a) z6+1+i=0, b) z2+2z+6=0
3) a) z2+1+i=0, b) z2+3z+4=0 13) a) z5-1=0, b) z2+z+1=0 23) a) z3-1+ 
, b) z2-z+5=0
4) a) z5+1=0, b) 2z2-2z+5=0 14) a) z6+1=0, b) z2+z+2=0 24)a) z4+1+ 
b) z2+3z+6=0
5) a) z6-1=0, b) 2z2+z+5=0 15) a) z7-1=0, b) 2 z2+z+1=0 25) a) z5-1- ; b) z2+z+4=0
6) a) z7+1=0; b) 2z2+3z+2=0 16) a) z8+1=0; b) z2+2z+3=0 26) a) z6+1- , b) z2+2z+4=0
7) a) z8-1=0; b) z2+3z+5 =0 17) a) z3+8=0; b) 3z2+2z+1=0 27) a) z3- 
, b) 3z2+z+1=0
8) a) z2-1+i=0; b) 2z2-z+5=0 18) a) z4-16=0; b) 2z2+z+6=0 28) a)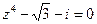 
; b) z2+z+7=0
9) a) z3-8=0; b) 3z2+3z+5=0 19) a) z3-1+i=0; b) z2+z+7=0 29) a) z3+ 
b) 6z2+2z+3=0
10) a) z4+16=0; b) z2+3z+6 =0 20) a) z4+1-i=0; b) 3z2+z+3=0 30) a) z3+ 
-i=0; b) 7z2+2z+4=0
Задача 3. Найти и построить на комплексной плоскости области, которым принадлежат точки
удовлетворяющие указанным условиям.
Данные к условию задачи, соответствующие вариантам:
27) 
