Функции комплексного переменного
Основные понятия
Пусть даны два множества Е и Д, элементами которых являются комплексные числа. Числа z=x+iy множества Д будем изображать точками комплексной плоскости z,а числа w=u+iv множества Е-точками комплексной плоскости W.
Если каждому числу z по некоторому правилу поставлено в соответствие определенное число w,то говорят, что на множестве определена однозначная функция комплексного переменного w=f(z),отображающая множество Д в множество Е (смотри рис.1)
Если каждому z соответствует несколько значений w, то функция w=f(z) называется многозначной.
Множество Д называется областью определения функции w=f(z); множество Е-областью значений функции.
Функцию w=f(z) можно записать в виде
u+iv=f(x+iy),
т.е.
f(x+iy)=u(x;y)+iv(x;y),
где
u=u(x,y)=Re f(z), v=v(x,y)=Jm f(z), (x,y)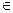 
D.
Функцию u(x;y) при этом называют действительной частью функции f(z), a v(x;y) – мнимой.
Пример 1. Найти действительную и мнимую части функции w=z2.
Решение.
Z=x+iy, то z 
=(x+iy) =(x -y )-i2xy. Тогда w=e 
* 
e 
=e (cos(-2xy)+isin(-2xy))=e cos2xy-ie sin2xy. Действительная часть функции равна u= е cos2xy, а мнимая часть равна v= (-e sin2xy).
Определение. Число w0 называется пределом функции w=f(z) в точке z0 (или при z 
z0),
если для любого положительного 
найдется такое положительное число, что для всех z 
z0,удовлетворяющих неравенству | z-z0|< 
, выполняется неравенство |f(z)-w0|< .
Записывают: 
f(z)=w0.Это определение коротко можно записать так:
(
Определение. Функция w=f(z) называется непрерывной в точке z 
,если 
Основные элементарные функции комплексного переменного.
Показательная функция.
Показательная функция w=e 
определяется формулой
(cosy+isiny).
Пример 2. Найти e 
.
В нашем примере z= 
Тогда
e =cos 
+isin =i
Логарифмическая функция
Обозначается w=Lnz. Можно доказать, что Lnz=ln 
+i(arg z+2 
k).
Эта формула показывает, что логарифмическая функция комплексного переменного имеет множество значений, т.е. это многозначная функция.
Пример 3. Вычислить Ln (-1).
Для числа z=-1 имеем z=1, arg z= .Следовательно,Lnz=ln1+i(
k)=i(
Пример 4. Вычислить ln2i.
Положив k=0, получим однозначную функцию, которую называют главным значением логарифма Lnz и обозначают символом lnz.
Имеем, ln2i=ln2i+iarg2i=ln2+i .
Пример 5. Найти Lni.
По формуле Lnz=lnz+i(argz+2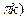 
,имеем Lni=lni+i(argi+2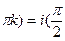 
+2 
+2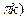
Степенная функция
Степенная фукция w=z 
с произвольным комплексным показателем a=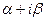 
определяется равенством
W=z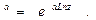 
Пример 6. Вычислить i 
i 
= 
.При к=0, i 
.
Тригонометрические функции
Тригонометрические функции комплексного аргумента z=x+iy определяются равенствами
cosz=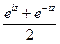 
, tgz= 
, ctgz= 
.
Пример 7. Вычислить sin i.
Sini= 
Гиперболические функции
Эти функции определяются равенствами
Sh z=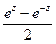 
, ch z= 
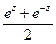, tgz= 
ctgz= 
.
Обратные тригонометрические и гиперболические функции
Эти функции определяются равенствами
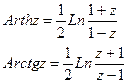g
Пример 8. Вычислить arctg 
.
Arctgz=-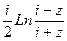 
;
Arctg 
=- 
.
Главное значение при к=0
arctg 
Упражнения
1.Вычислить arccosi.
2. Вычислить i 
3. Найти действительную и мнимую части функции w=sinz
4. Найти значение модуля функции w=sinz в точке z= 
Комплексные числа
Комплексное число это упорядоченная пара действительных чисел (x,y).Записывается
Z=x+iy, где x-действительная часть числа, y-мнимая часть числа, i-мнимая единица,
i 
Числа 
и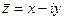 
называются сопряженными.
Комплексные числа можно складывать, вычитать, умножать, делить.
Пусть 
то 
Замечание. При деление комплексных чисел числитель и знаменатель умножают на сопряженный знаменатель.
Пример. Выполнить действия: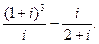 
+ + 
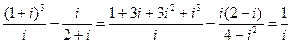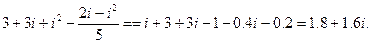
Упражнение. Выполнить действия: 
