Исследование функций и построение графиков
Общая схема исследования функции
- Область определения
- Нули функции
- Четность
- Периодичность
- Наличие асимптот
- Монотонность функции
- Экстремумы
- Выпуклость функции
- Точки перегиба
Асимптоты
Вертикальная асимптота функции 
- это прямая x=a такая, что хотя бы один из односторонних пределов равен 
. Например, функция
Имеет вертикальную асимптоту х=2
Наклонная асимптота функции - это прямая y=ax+b такая, что предел разности между значениями функции и этой прямой равен 0 при 
. Например, функция
Имеет наклонную асимптоту 
Необходимые и достаточные условия экстремума функции
Для нахождения экстремума функции требуется:
· определить точки, в которых он возможен (точки, подозрительные на экстремум)
· выяснить, действительно ли он имеет место
· распознать характер экстремума
Критическими точками будем называть такие точки, в которых функция может иметь экстремум. А это точки, в которых производная равна 0 или не существует. При этом стационарной точкой обычно называют такую точку х0, в которой производная (скорость) равна нулю:
f ‘ (х0) = 0
Первое достаточное условие
Пусть непрерывная функция f (х) дифференцируема в δ- окрестности точки х0, за исключением, может быть, самой этой точки.
Если в этой точке производная меняет знак, то имеет место локальный экстремум.
Ниже на рисунке 6 изображен график функции 
Рис. 6
Пусть для определенности
f ’ (х0 – 0) < 0, а f ‘(х0 + 0) > 0.
Покажем, что в этом случае имеет место минимум. Воспользуемся формулой Лагранжа:
f (х0 + ∆х) – f (х0) ~ f’ (х0) ∆х.
В левой окрестности: ∆ х < 0, f’ (х0 + ∆х) < 0,
а значит, f (х0 + ∆х) > f (х0).
В правой окрестности: ∆ х > 0, f’ (х0 + ∆х) > 0,
и значит, f (х0 + ∆х) > f (х0).
Изображённая на рисунке функция не имеет производной в точке минимума (угол).
Если в критической точке производная функции меняет знак с минуса на плюс, то имеет место минимум, а если с плюса на минус - максимум.
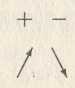
min max
Первое достаточное условие годится для любых критических точек и является универсальным.
Второе достаточное условие
Пусть функция f (x) дважды дифференцируема на отрезке [ а, b ] и имеет на этом отрезке стационарную точку (f ’ (х0) = 0).
Если в этой точке вторая производная отлична от нуля, то имеет место локальный экстремум.
Формула Тейлора
f (x) = f (х0) + 
в стационарной точке принимает вид:
f (x) = f (х0) +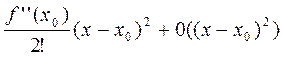 
.
Так как в любой окрестности х0 (правой и левой) (х — х0)2 > 0, то в δ -окрестности точки х0 выполняются неравенства:
если f" (x0) > 0, то f (х) > f (х0) – 
min
если f" (x0) < 0, то f (х) < f (х0) – 
max
Итак, если вторая производная в стационарной точке больше нуля, то имеет место минимум, а если меньше нуля, то максимум.
Выпуклость функции
При исследовании функции и построении ее графика, помимо экстремума, используется ещё несколько важных понятий.
Выпуклость вверх и вниз
Функция f (x) имеет выпуклость вверх (вниз) в точке x0, если касательная в окрестности этой точки располагается выше (ниже) этой кривой.
Задача 1
Пусть функция f (x) непрерывна и имеет производные первого и второго порядка.
Показать, что по знаку производной второго порядка можно судить о том, функция в этой точке выпукла вверх или вниз.
Формулу Тейлора
f (x) = 
можно записать в следующем виде:
f (x) ~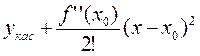 
(*)
По определению, если f (x) < укас, то функция выпукла вверх, а если f (x) > укас, то функция выпукла вниз. Таким образом из формулы (*) следует:
f" (x0) > 0 — выпуклость вниз
f" (x0) < 0, 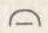— выпуклость вверх ◄
Точка х0 называется точкой перегиба, если она разделяет у непрерывной функции области выпуклости вверх и вниз.
Вопрос: Индентифицируйте точки А, В, С, заданные на рисунке.
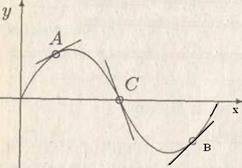
Ответ: А — точка выпуклости вверх, В — точка выпуклости вниз, С — точка перегиба.
● Проходящая через точку перегиба касательная, частично лежит выше кривой, а частично ниже.
Необходимые условия точки перегиба: критические точки
Критическими точками 2 рода мы будем называть такие точки, в которых функция может иметь перегиб.
Точка х0 является критической точкой относительно перегиба, если выполняется одно из двух условий:
1. f" (x0) = 0,
2. f" (x0) — не существует или обращается в ∞.
