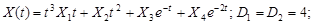Говорят, что случайная функция Х (t) сходится в среднеквадратическом при 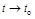 к случайной величине Х о, если начальный момент второго порядка
к случайной величине Х о, если начальный момент второго порядка  стремится к нулю при t ® t о:
стремится к нулю при t ® t о:
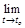
 = 0.
= 0.
Сходимость в среднеквадратическом обозначается символом

Случайная функция Х (t) называется непрерывной в среднеквадратическом в точке t о, если

Производной случайной функции X (t) называется случайная функция X ¢(t), определяемая как предел в среднеквадратическом отношения приращения случайной функции к приращению неслучайного аргумента:

Для дифференцируемости случайной функции необходимо, чтобы функция X (t)была непрерывной, а для этого непрерывной должна быть ее корреляционная функция. Достаточным условием дифференцируемости функции X (t)в точке t является существование второй смешанной частной производной корреляционной функции при равных значениях ее аргументов.
Интегралом в среднеквадратическом от случайной функции X (t) в постоянных границах от a до b называется предел соответствующей интегральной суммы
 ,
,
где l- наибольший из всех D ti, а предел понимается в смысле среднеквадратического.
Линейным однородным преобразованием случайной функции X (t) называется преобразование L о, обладающее следующими свойствами:
1о. L о[ X 1(t) + X 2(t)]= L о[ X 1(t)] + L о[ X 2(t)];
2о. L о[ CX (t)] = CL о[ X (t)].
Примерами линейных однородных преобразований могут служить:
а) оператор дифференцирования  ;
;
б) оператор интегрирования  ,
,
где операции дифференцирования и интегрирования следует понимать в «среднеквадратическом»;
в) оператор умножения случайной функции на неслучайную
Y (t) = j(t) X (t);
г) оператор интегрирования с заданным «весом» 
 .
.
Линейным неоднородным называется преобразование вида
Y (t) = L о[ X (t)] + f (t),
где f (t)- неслучайная функция.
Каноническим разложением случайной функции называется сумма ее математического ожидания и взаимно некоррелированных элементарных случайных функций
 , (9.4)
, (9.4)
где случайные величины  имеют математические ожидания, равные нулю, и называются коэффициентами канонического разложения, а неслучайные функции
имеют математические ожидания, равные нулю, и называются коэффициентами канонического разложения, а неслучайные функции  - координатными функциями.
- координатными функциями.
Корреляционная функция канонического разложения имеет вид
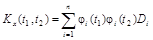 . (9.5)
. (9.5)
При t 1 = t 2 = t  . (9.5а)
. (9.5а)
9.17. На RC - цепочку, изображённую на рис. 9.1, подаётся
случайное напряжение X (t) c характеристиками  и
и  Найти математическое ожидание, корреляционную функцию и дисперсию напряжения Y (t) на выходе цепочки.
Найти математическое ожидание, корреляционную функцию и дисперсию напряжения Y (t) на выходе цепочки.
|
¢ Дифференциальное уравнение, описывающее связь между входным и выходным напряжениями RC - цепочки, составляется на основе закона Кирхгофа и имеет вид
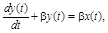
Решая это уравнение при нулевом начальном условии методом вариации произвольных постоянных, получим:

Таким образом, случайный процесс Y (t) является результатом применения к случайной функции X (t) линейного однородного оператора

Значит, 
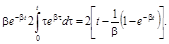
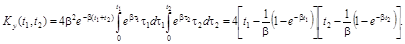 Дисперсия процесса на выходе равна
Дисперсия процесса на выходе равна 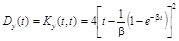 . £
. £
9.18. На вход дифференцирующего устройства поступает случайный процесс X (t) с математическим ожиданием 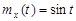 и корреляционной функцией
и корреляционной функцией  где
где  - постоянная дисперсия X (t). Определить математическое ожидание и дисперсию на выходе системы.
- постоянная дисперсия X (t). Определить математическое ожидание и дисперсию на выходе системы.
¢ Реакция 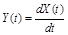 имеет характеристики
имеет характеристики 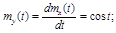

Полагая  , находим дисперсию
, находим дисперсию 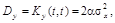 которая зависит от
которая зависит от  и от коэффициента
и от коэффициента  характеризующего быстроту затухания корреляционной связи между сечениями случайной функции X (t) при возрастании промежутка между ними.
характеризующего быстроту затухания корреляционной связи между сечениями случайной функции X (t) при возрастании промежутка между ними.
При малых значениях  корреляционная связь затухает медленно, поэтому случайные функции X (t) и Y (t) изменяются со временем сравнительно плавно. Следовательно, дифференцирование X (t) приводит к незначительным ошибкам.
корреляционная связь затухает медленно, поэтому случайные функции X (t) и Y (t) изменяются со временем сравнительно плавно. Следовательно, дифференцирование X (t) приводит к незначительным ошибкам.
Если же величина  велика, корреляционная функция
велика, корреляционная функция 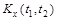 убывает быстро, в составе случайной функции X (t) преобладают резкие беспорядочные колебания, значит, дифференцирование такой функции приведет к большим погрешностям. £
убывает быстро, в составе случайной функции X (t) преобладают резкие беспорядочные колебания, значит, дифференцирование такой функции приведет к большим погрешностям. £
9.19. Случайная функция X (t) задана каноническим разложением:

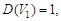

Найти математическое ожидание, дисперсию и корреляционную функцию процесса 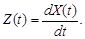
¢ Запишем каноническое разложение случайного процесса Z (t):

Отсюда следует, что  координатные функции
координатные функции 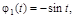

Каноническое разложение корреляционной функции  имеет вид
имеет вид

или  .
.
Тогда дисперсия процесса будет равна 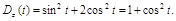 £
£
9.20 – 9.29. На вход динамической системы поступает случайный сигнал X (t), характеристики которого известны. Работа системы описывается оператором L. Определить характеристики случайной функции Y (t).
9.20. 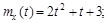


9.21. 


9.22. 
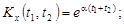
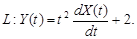
9.23. 

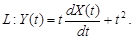
9.24. 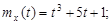

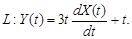
9.25. 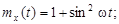
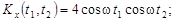

9.26. 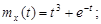
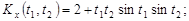
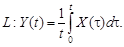
9.27. 
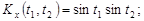
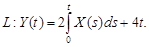
9.28. 
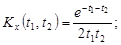

9.29. 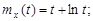


9.30 – 9.34. Найти характеристики случайной функции X (t), заданной своим каноническим разложением.
9.30. 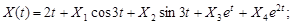
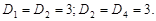
9.31. 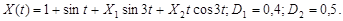
9.32. 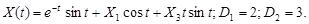
9.33. 
9.34.