9.1. Законы распределения и основные характеристики случайных функций
Случайной функцией называют функцию одного или нескольких аргументов, значение которой при фиксированных значениях аргументов является случайной величиной. Например, X (t) – случайная функция одного аргумента, если каждому значению t из некоторого множества поставлена в соответствие случайная величина X (t). Если параметр t играет роль времени, то случайная функция называется случайным процессом.
Реализацией случайной функции X (t) называется неслучайная функция x (t), полученная в результате испытания в заданных условиях.
Пусть над случайной функцией произведено n испытаний, в результате чего получено n реализаций 
Тогда при некотором фиксированном значении аргумента t = t o эти реализации превратятся в значения случайной величины Х (t о), которую называют сечением случайной функции. Ее закон распределения F 1(x / t о) является одномерной функцией распределения даннойслучайной функции X (t) при фиксированном t = t o. Соответствующая одномерная плотность существует, если сечение X (t о) является непрерывной случайной величиной, при этом в точках дифференцируемости функции F 1(x / t о) справедливо равенство
Двумерной функцией распределения 
называется функция совместного распределения двух сечений 
случайной функции:
Соответствующая двумерная плотность существует, если двумерная случайная величина 
непрерывна, и если при этом в точке (x, y) функция дважды дифференцируема, то
Отсюда 
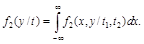
Основными характеристиками случайных функций являются математи-ческое ожидание, дисперсия и корреляционная функция.
Математическим ожиданием и дисперсией случайной функции X (t) называются такие неслучайные функции 
которые для каждого фиксированного значения t равны математическому ожиданию и дисперсии соответствующего сечения.
Для случайной функции непрерывного типа
. (9.1)
(9.2)
Корреляционной функцией называется неслучайная функция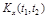 
двух действительных аргументов t 1 и t 2 , которая для каждой пары фиксированных t 1 и t 2 равна корреляционному моменту соответствующих сечений:
(9.3)
Нормированная корреляционная функция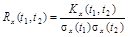 
по смыслу аналогична коэффициенту корреляции двух сечений случайной функции.
Основные свойства корреляционной функции:
1. 
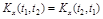- свойство симметрии.
2. 
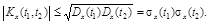
3. Если Y (t) = X (t) + j(t), где j(t)- неслучайная функция, то
.
4.Если Y (t) = j(t) X (t), где j(t) - неслучайная функция, то
.
Взаимной корреляционной функцией 
двух действительных случайных функций 
называется неслучайная функция двух аргументов, равная корреляционному моменту данных случайных функций:
9.1. Случайная функция X (t) задана в виде X (t) = Vt + b, где V - случайная величина непрерывного типа, распределенная по нормальному закону 
а b - неслучайная константа. Найти одномерную плотность 
и основные характеристики процесса: 
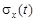и 
¢ Зафиксируем значение аргумента t, тогда X (t) станет функцией лишь случайной величины, плотность распределения которой нормальна:
Функция 
монотонно возрастает всюду, поэтому справедливо равенство
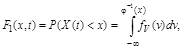откуда следует, что
Так как 
то
.
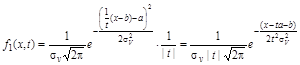Отсюда получаем: 
£
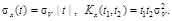9.2. Случайная функция 
где U – случайная величина, возможные значения которой принадлежат интервалу (0;10). Найти реализации функции X (t) в двух испытаниях, в которых U приняла значения: а) 
; б) 
9.3. Случайная функция 
где U –случайная величина дискретного типа, закон распределения которой имеет вид:
| X | ||||
| P | 0,2 | 0,5 | 0,2 | 0,1 |
Найти сечения X (t), соответствующие фиксированным значениям аргумента: а) 
б)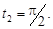 
9.4. Доказать, что неслучайный множитель можно выносить за знак математического ожидания:
9.5. Доказать, что математическое ожидание суммы двух случайных функций равно сумме математических ожиданий слагаемых.
9.6. Найти математическое ожидание случайной функции:
а)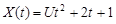 
,
б)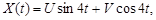 
где U, V - случайные величины, причем M (U) = M (V) = 1.
9.7. Доказать, что при равных между собой значениях аргументов корреляционная функция случайной функции X (t) равна её дисперсии: 
9.8. Доказать, что от прибавления к случайной функции X (t) неслучайной функции j(t) корреляционная функция не изменится: если Y (t) = X (t) +j(t), то 
9.9. Доказать, что при умножении случайной функции X (t) на неслучайный множитель j(t) корреляционная функция умножается на произведение: 
9.10. Случайный процесс X (t) имеет вид 
где V - случайная величина, равномерно распределенная на [0;3]. Найти одномерную функцию и плотность этого процесса.
9.11. Случайная функция X (t) задана в виде X (t) = U + Vt, где U и V - независимые случайные величины, подчиняющиеся одному и тому же закону распределения N (m,s). Записать одномерную плотность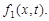 
Найти 
9.12. Случайное гармоническое колебание задано в виде 
где w - неслучайная частота, а случайные амплитуды A и B независимы и подчиняются каждая нормальному закону N (0;s). Найти одномерную и двумерную плотности процесса.
9.13. Одномерная плотность вероятности случайного процесса X (t) имеет вид
где a и s - постоянные величины, причём s> 0.
Найти: а) 
б) вероятность неравенства 
9.14. Случайный процесс задан выражением 
где V - случайная величина, плотность вероятности которой
- неслучайная функция. Найти 
9.15. Случайный процесс X (t) представляет собой случайную ступеньку
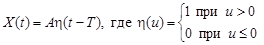- единичная функция Хевисайда, A - случайная амплитуда с характеристиками 
Т - случайное, независимое от A время начала ступеньки, с плотностью распределения 
Найти математическое ожидание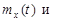 
корреляционную функцию 
9.16. Угол крена корабля X (t) представляет собой нормальный случайный процесс с характеристиками 
Известно, что в момент времени 
угол крена корабля составлял 
градусов. Какова вероятность того, что в момент 
угол крена будет больше, чем b градусов?
