Готовимся к контрольной работе

Министерство здравоохранения Украины Национальный медицинский университет Имени А. А. Богомольца

РАБОЧАЯ ТЕТРАДЬ
Для самостоятельной работы студентов

Учебная дисциплина: "Медицинская и биологическая физика"
Направление: медицина
Специальность: "Лечебное дело", "Педиатрия", "Медико-профилактическое дело", "Медицинская психология","Стоматология"

 

 

Кафедра Медицинской и биологической физики

Авторы: А.В.Чалый, Н.В.Стучинська, И.Ф.Марголыч
Утверждено на заседании кафедры от 31.08.2015 г.,протокол № __1__
Рассмотрено и утверждено: ЦМК из физ.- хим. дисциплин
от " 1.09 " 2015 года, протокол № 1

Тема 2. " Интегральное исчисление"

Вступление. Целью рабочей тетради является помощь в усвоении студентами основных понятий интегрального исчисления. Студенты должны усвоить понятие определенного и неопределенного интегралов, понимать их физическое и геометрическое содержание, получить знание об основных методах интегрирования, научиться находить неопределенные и вычислять определенные интегралы методом замены переменной, подстановкой и интегрирование частями.

Знания основ и интегрального исчисления и умения находить самые простые интегралы является необходимой предпосылкой для усвоения методов развязывания дифференциальных уравнений, с помощью которых моделируют много процессов в живых организмах, медицине, биологии, фармации.

В рабочей тетради студентам предлагаются разные за сложностью задания для самостоятельной проработки. Критериями оценивания самостоятельной работы студента являются: оформлена рабочая тетрадь, умение решать задание из рабочей тетради и умения решать подобные за сложностью задания, которые предлагаются преподавателем на практическом занятии. Для объективного оценивания самостоятельной работы студентам рекомендуется детально описывать все этапы выполнения заданий.

Тема 2. Основы интегрального исчисления (неопределенный и определенный интегралы, методы интегрирования)

Цель: усвоить понятия первообразной и интеграла;

- ознакомиться с основными методами интегрирования.

- ввести понятие определенного интеграла;

- научить применению интеграла к развязыванию физических задач и задач медико-биологического устремления, вычисления площадей и объемов.

Знать:

· определения первообразную, интеграла

· понимать содержание операции интегрирования как обратной к операции дифференцирования;

· геометрическое и физическое содержание интеграла;

· основные методы интегрирования.

· Уметь: находить первобытные и самые простые интегралы

· пользуясь таблицей и правилами нахождения первобытных;

· использовать метод замены переменной, подстановки и интегрирования

· частями; находить первобытные и вычислять определенные интегралы

· на основе формулы Ньютона-Лейбница;

· делать замену переменной в определенном интеграле;

Основные понятия темы: первообразная, неопределенный интеграл, метод замены переменной, интегрирования частями, определенный интеграл, формула Ньютона-Лейбница.

.

Рекомендована література

1.Чалий О.В., Стучинська Н.В., Меленевська А.В. Вища математика. Навчальний посібник для студентів вищих медичних і фармацевтичних закладів.. – К.: Техніка, 2001. – С.80-103.

2.Медична і біологічна фізика.Т.1./ За ред. О.В.Чалого. – К.: Віпол, 1999.

3.Ремизов А.Н. Математическая и биологическая физика.-М.:”Высшая школа»,1987. с. 610-620

4. Ремизов А.Н. Исакова Н.Х., Максина А.Г. Сборник задач по медицинской и биологической физике. - М.: «Высшая школа», 1987. с. 610-620

5. Баварин И.И. Высшая математика. – М.: Просвещение, 1980. с. 102-142

6. Свердан П.Л. Вища математика: Аналіз інформації у математиці та медицині. – Львів: Світ, 1998.

7. Лобоцкая Н.Л., Мороз Ю.В., Дунаев А.А. Высшая математика: Учебник для вузов. – М.:Высш.шк.,1978.

 

Вопросы для теоретического обработки:

1. Что такое производная функции?
2. Что называют дифференциалом?
3. Какую функцию называют первообразная?
4. Какое количество первообразных имеет каждая функция, имеющая хотя бы одну первоначальную?
5. Дайте определение неопределенного интеграла
6. Приведите примеры функциональных зависимостей, встречающихся в живой и неживой природе. Какой физический смысл имеют первоначальные этих функций?
5. Сформулируйте определение определенного интеграла.
6.Дайте геометрическое толкование определенного интеграла.
7. Запишите формулу Ньютона-Лейбница.
8.Сформулюйте свойства неопределенного интеграла.

 

Задача для самостоятельной работы темы:

Задача 1. Запишите первообразкая для таких функций (проверьте правильность, используя правила дифференцирования)

х³ 1/sin²x

e^x 1/(x² + 1)

sin x 1/(x² - 1)

cos x 1/x

Задача 2. Найти интегралы, превращая выражения должным образом

1.

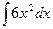
2.

3.

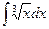
4.

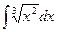
5.

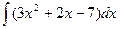
6.

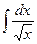
8.

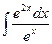
9.

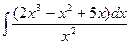
10.

Задача 3. Знайдить интегралы методом замены переменной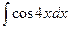

1.

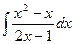
2.

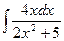
3.

4.

5.

6.

7.

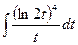
8.

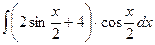
9.

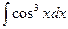
10.

11.

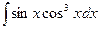
Задание 4. Найти интегралы методом интегрирования по частям.1. .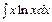

2. .

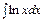3. .

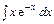4. .

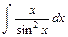5. .

6. .

7. .

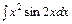8. .

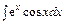Задача 5. Знайти визначений інтеграл:

1.
2.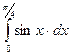
3.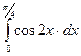
4.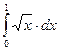
5.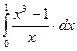
6.

Задача 6. Знайти визначений інтеграл, зробивши заміну змінної

1.
2.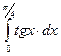
3.
4.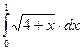
5.
6.
7.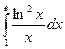

Готовимся к контрольной работе

Найдите интегралы:

1.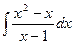
2.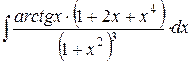
3.
4.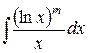
5.
6.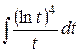
7.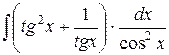
8.
9.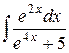
10.
11.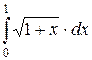
12.
13.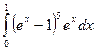
14.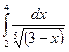

Задача для СРС

Тема практического занятия	Аудиторная самостоятельная работа студента	Время подготовки студента к занятию (ч)	Формы внеаудиторной самостоятельной работы
Обязательные и одинаковые для всех студентов	За вибором студента
Основы интегрального исчисления	Нахождение неопределенного и определенного интегралов, овладение основными методами интегрирования: методом замены переменной, интегрирование по частям	3,4	Решение задач, примеров, предложенных тетради. Оформление рабочей тетради. Задача 1-3 и теоретические вопросы должны быть проработаны студентом к проведению практического занятия «Интегральное исчисление».	Решение задач, примеров, не представленные в данном тетради из литературных источников по выбору студента и рекомендации преподавателя.