РАБОЧАЯ ТЕТРАДЬ
Для самостоятельной работы студентов
Учебная дисциплина: "Медицинская и биологическая физика"
Направление: медицина
Специальность: "Лечебное дело", "Педиатрия", "Медико-профилактическое дело", "Медицинская психология","Стоматология"
Кафедра Медицинской и биологической физики
Авторы: АО.В.Чалый, Н.В.Стучинська, И.Ф.Марголыч
Утверждено на заседании кафедры от 31.08.2015 г.,протокол № __1__
Рассмотрено и утверждено: ЦМК из физ.- хим. дисциплин
от " 1.09 " 2015 года, протокол № 1
Вступление. Целью рабочей тетради является помощь в усвоении студентами понятия дифференциала, производной функции, формирование понятия о функциях нескольких переменных, частные производные и полный дифференциал. Студенты должны научиться дифференцировать функции одной и нескольких переменных, находить полные дифференциалы функций. Особенно важным является усвоение правила дифференцирования составленных функций. С этой целью студентам предложены разные за сложностью развязывания задания. Эти задания поданы в порядке осложнения. Критериями оценивания выполнения указанных заданий будет умение студентом продемонстрировать не только решение заданий тетради для самостоятельной работы студента, но и подобных за сложностью и предложенных преподавателем при проверке выполненных самостоятельно. Для правильного ведения тетради предлагается студентам детально расписывать все этапы выполнения предложенных заданий.
Тема 1. " Основы дифференциального исчисления"
Цель: усвоить понятие дифференциала, производной функции, сформировать понятие функции нескольких переменных, частных производных и полных дифференциалов.
Знать: - определение дифференциала функции;
- определение производной функции;
- функция нескольких переменных;
- определение частных производных;
- определения полного дифференциала;
- производные высших порядков;
- применение производных и дифференциалов.
Уметь: - находить производную функции;
- находить дифференциал функции;
- находить частные производные;
- вычисления полного дифференциала функций нескольких переменных;
- находить производные высших порядков;
- применять дифференциалы функций для приближенных вычислений и погрешностей
Основные понятия темы: производная функции, дифференциал функции, производные высших порядков, частных производных функции многих переменных, полный дифференциал функции многих переменных.
Рекомендованная литература
1. Медицинская и биологическая физика: Учебник для студентов высших мед. учебных завед. IV уровня аккред. /А.В. Чалый, Я.В. Цехмистер, Б.Т.Агапов и др.; Под редакцией А.В.Чалого. – Винница: Нова Кныга, 2011. - 568 с.
2. Ремизов А.Н. Медицинская и биологическая физика.-М.: Высшая школа, 1999. – 616 с.
3. Ремизов А.Н. Исакова Н.Х., Максина А.Г. Сборник задач по медицинской и биологической физике. - М.: Высшая школа, 1987.
4. Баварин И.И. Высшая математика. – М.: Просвещение, 1980.
5. Лобоцкая Н.Л., Мороз Ю.В., Дунаев А.А. Высшая математика: Учебник для вузов. – М.: Высш.школа, 1978.
Вопрос для теоретической проработки:
1. Дайте определение производной функции.
2. Дайте физическую интерпретацию производной.
3. Дайте геометрическую интерпретацию производной.
4. Сформулируйте основные правила дифференцирования.
5. Как дифференцировать сложную функцию?
6. Дайте определение производной второго и высших порядков.
7. Что называют дифференциалом функции?
8. Приведите примеры (желательно из биологии и медицины) функций двух и большего числа независимых переменных.
9. Дайте определение функции нескольких переменных.
10. Дайте определение частных производных функции нескольких переменных.
11. Что называют полным дифференциалом функции нескольких переменных?
Задание для самостоятельной проработки темы:
Задание 1. Найти производные таких функций:
1. 
2. 
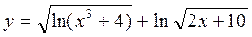
3. 
4. 
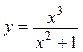
5. 
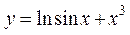
6. 
7. 
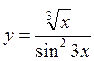
8. 
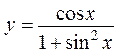
9. 
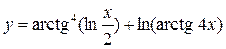
10. 
11. 
12. 
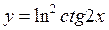
13. 
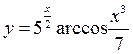
14. 
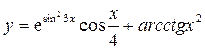
15. 
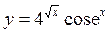
16. 
Задание 2. Найти дифференциалы таких функций
1. 
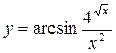
2. 
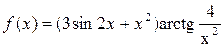
3. 
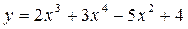
4. 
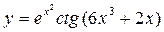
5. 
6. 
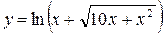
7. 
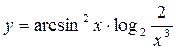
8. 
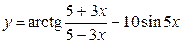
9. 
10. 
11. 
12. 
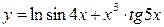
13. 
14. 
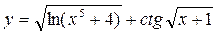
15. 
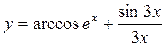
Задание 3. Найти частные производные функций
1. 
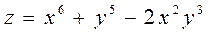
2. 
3. 
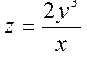
4. 
+ 
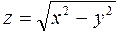5. 
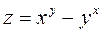
6. u= 2 x ln y+ 
7. z = y 
ln x
8. u= x tg 
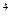y
9. 
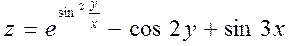
10. 
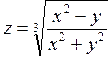
11. 
12. u = (xy) z
13. u = zxy + y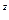 
14. 
15. u = log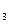 
(x 3 y) - tgy
16. 
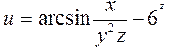
Задание 4. Найти полные дифференциалы функций
1. 
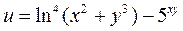
2. z =2 x3 + 3y3 – 3xy
3. z = x 2 y 3 - arccos 
4. 
5. 
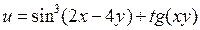
6. 
7. z = 4sin2 y + cos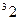 
x
8. z=arctg 
- yxy
9. z= arcsin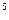 
10. 
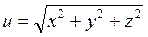- log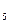 
(
)
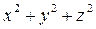11. 
+ 
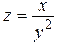12. u = z× x× y - z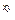 
13. z = ln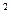 
(x 2 +y 2) 
14. u= arctg 
15. z = lncos3(x 4 y 3) – sin 
16. 
.
17. Показать, что относительная погрешность в 1 % при определении радіуса дает относительную погрешность приблизительно в 2 % при вычислении площади круга и поверхности сферы.
18. Найти выражение для относительной погрешности величины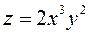 
, если x и y находятся непосредственно.
Задание для СРС
| Тема практического занятия | Аудиторная самостоятельная работа студента | Время подготовки студента до занятия | Формы внеаудиторной самостоятельной работы | |
| Обязательные и одинаковые для всех студентов | За выбором студента | |||
| Основы дифференциального исчисления | Нахождение производных функций, нахождения дифференциалов функций, нахождения частных производных функций, вычисления полного дифференциала функций нескольких переменных, нахождение производных высших порядков, применения дифференциалов функций для приблизительных вычислений и погрешностей | 3,4 | Развязывание заданий, примеров, предложенных студентам в тетради, оформление рабочей тетради для самостоятельной работы студента | Развязывание заданий, примеров, которые не поданы в данной тетради из литературных источников за выборомстудента |
