· Равенство («
»), тривиальное отношение эквивалентности на любом множестве, в частности, вещественных чисел.
· Сравнение по модулю, («а ≡ b (mod n)»).
· В Евклидовой геометрии
· Отношение конгруэнтности («
»).
· Отношение подобия(«
»).
· Отношение параллельности прямых («
»).
· Эквивалентность функций в математическом анализе:
Говорят, что функция 
эквивалентна функции 
при 
, если она допускает представление вида 
, где 
при . В этом случае пишут 
, напоминая при необходимости, что речь идет о сравнении функций при . Есл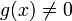и 
при 
, эквивалентность функций и при , очевидно, равносильна соотношению 
.
· Отношение равномощности множеств.
Факторизация отображений
Множество классов эквивалентности, отвечающее отношению эквивалентности 
, обозначается символом 
и называется фактор-множеством относительно . При этом сюръективное отображение
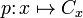
называется естественным отображением (или канонической проекцией) 
на фактор-множество .
Пусть , 
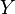— множества, 
— отображение, тогда бинарное отношение 
определённое правилом
является отношением эквивалентности на . При этом отображение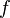 
индуцирует отображение 
, определяемое правилом
или, что то же самое,
.
При этом получается факторизация отображения 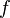на сюръективное отображение 
и инъективное отображение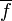 
.
12. Понятие о функциональном отношении. Определения функции и отображения, композиция функций. Теорема об ассоциативном свойстве операции композиции отображений.
Функция — двухместное отношение R, определенное на некотором множестве, отличающееся тем, что каждому значению x отношения xRy соответствует лишь одно-единственное значение y. Пример: «y отец x». Свойство функциональности отношения R записывается в виде аксиомы: (xRy и xRz)→(y ≡ z). Поскольку каждому значению x в выражениях xRy и xRz соответствует одно и то же значение, то y и z совпадут, окажутся одними и теми же. Функциональное отношение однозначно, поскольку каждому значению x отношения xRy соответствует лишь одно-единственное значение y, но не наоборот.
Теорема:
Операция композиции на множестве всех преобразований непустого множества ассоциативна. То есть, если даны отображения f:X->Y, g:Y->Z и h:Z->T, то fo(goh)=(fog)oh.
Доказательство:
Ясно, что композицию fo(goh) можно разложить на два действия. Сначала выполним композицию g и h, а затем, композицию f и полученного результата. Распишем композицию goh:
goh = Y->Z o Z->T=Y->T.
Далее, распишем композицию f с полученным результатом:
fo(goh)= X->Y o Y->T = X->T.
таким образом, мы получили отображение из X в T.
Теперь, рассмотрим композицию (fog)oh. Ее аналогично можно разбить на два этапа. Сначала произведем композицию f и g, а затем композицию полученного результата и h. Распишем композицию f и g:
fog= X->Y o Y->Z = X->Z.
Далее, композицию полученного результата и h:
(fog)oh= X->Z o Z->T = X->T.
Можно заметить, что fo(goh)=(fog)oh.
Теорема доказана.
13. Способы задания функций. Таблица функции, заданной на конечном множестве. График функции. Число различных функций и отображений на конечном множестве в конечное множество (с доказательством).
Способы задания функции
Аналитический способ
Функция, как математический объект, представляет собой бинарное отношение, удовлетворяющее определенным условиям. Функцию можно задать непосредственно как множество упорядоченных пар, например: 
есть функция 
. Однако, этот способ совершенно непригоден для функций на бесконечных множествах (каковыми являются привычные вещественные функции: степенная, линейная, показательная, логарифмическая и т. п.).
Для задания функции пользуются выражением: 
. При этом, 
есть переменная, пробегающая область определения функции, а 
— область значений. Эта запись говорит о наличии функциональной зависимости между элементами множеств. х и y могут пробегать любые множества объектов любой природы. Это могут быть числа, векторы, матрицы, яблоки, цвета радуги. Поясним на примере:
Пусть имеется множество 
яблоко, самолет, груша, стул 
и множество 
человек, паровоз, квадрат . Зададим функцию f следующим образом: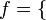 
(яблоко, человек), (самолет, паровоз), (груша, квадрат), (стул, человек) . Если ввести переменную x, пробегающую множество и переменную y, пробегающую множество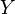 
, указанную функцию можно задать аналитически, как: .
Аналогично можно задавать числовые функции. Например: 
, где х пробегает множество вещественных чисел, задает некоторую функцию f. Важно понимать, что само выражение не является функцией. Функция, как объект, представляет собой множество (упорядоченных пар). А данное выражение, как объект, есть равенство двух переменных. Оно задает функцию, но не является ею.
Однако, во многих разделах математики, можно обозначать через f(x) как саму функцию, так и аналитическое выражение, ее задающее. Это синтаксическое соглашение является крайне удобным и оправданным.
Графический способ
Числовые функции можно также задавать с помощью графика. Пусть 
— вещественная функция n переменных.
Рассмотрим некоторое (n+1)-мерное линейное пространство над полем вещественных чисел (так как функция вещественная). Выберем в этом пространстве любой базис (
). Каждой точке функции сопоставим вектор: 
. Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
Если в качестве линейного пространства взять евклидово пространство свободных геометрических векторов (направленных отрезков), а число аргументов функции f не превосходит 2, указанное множество точек можно изобразить наглядно в виде чертежа (графика). Если сверх того исходный базис взять ортонормированным, получим «школьное» определение графика функции.
Для функций 3 аргументов и более такое представление не применимо ввиду отсутствия у человека геометрической интуиции многомерных пространств.
Однако, и для таких функций можно придумать наглядное полугеометрическое представление (например каждому значению четвертой координаты точки сопоставить некоторый цвет на графике).
Таким общим вопросом, например, является вопрос о сравнении множеств по мощности: если между двумя множествами существует взаимно однозначное отображение (биекция), то два данных множества называют эквивалентными или равномощными Это позволяет провести классификацию множеств в виде единой шкалы, начальный фрагмент выглядит следующим образом:
· конечные множества — здесь мощность множества совпадает с количеством элементов;
· счётные множества — множества эквивалентные множеству натуральных чисел;
· множества мощности континуума (например, отрезок действительной прямой или сама действительная прямая).
В соответствии с этим, имеет смысл рассматривать следующие примеры отображений:
· конечные функции — отображения конечных множеств;
· последовательности — отображение счётного множества в произвольное множество;
· континуальные функции — отображения несчётных множеств в конечные, счётные или несчётные множества.
14. Определение образа подмножества относительно функции. Теорема об образе объединения и пересечения подмножеств относительно отображения.
