Кафедра методики фізики і загальнотехнічних дисциплін
 |
Методичний посібник

Миколаїв – 2005
Основні елементи алгебри логіки
Для викладу матеріалу, присвяченого фізичним основам обчислювальної техніки, слід ознайомитися з теоретичною стороною цього питання.
У теорії електронно-обчислювальної техніки широко використовується математичний апарат алгебри логіки (булевої алгебри). Це пов’язано з тим, що змінні величини (аргументи і функції), що розглядаються в ній, можуть приймати тільки два значення: «істинно» (логічна 1) і «помилково» (логічний 0). Такі величини прийнято називати двійковими. Отже, і система числення, використовувана в арифметичних і логічних пристроях цифрової техніки – двійкова (має всього дві цифри: «0» і «1»).
Існуючі функції в алгебрі логіки називаються логічними. Логічні функції У декількох змінних (X0, Х1,... Хn–1) визначають характер логічних операцій, в результаті яких набору змінних ставиться у відповідність змінна Y
Y = f (X0, Х1,...Хn–1).
Основними логічними пункціями алгебри логіки є:
– логічне складання (диз’юнкція);
– логічне множення (кон’юнкція);
– логічне заперечення (інверсія).
Розглянемо ці функції.
Логічне складання (диз’юнкція)
При логічному складанні два або більш висловів, вхідних змінних сполучають сполучником «АБО» (число аргументів (доданків Х.) може бути будь-яким). Позначають цю операцію символом «Ú» або знаком складання (+) і записується вона у вигляді:
Y = Х1+ Х2
або:
Y = Х1 Ú Х2.
Запис формулюється таким чином: Y рівний Х1 АБО Х2. Це значить, що функція Х1+ Х2 приймає значення логічної 1, якщо істинне хоча б одне на доданках Х1 або Х2. І лише у разі, коли доданки Х рівні 0, результат складання Y також рівний 0.
Найбільш наочно функція перетворення характеризується таблицею, в рядках якої приведені всілякі варіанти комбінацій аргументів X і відповідні їм значення Y. Така таблиця називається таблицею істинності. Число різних комбінацій значень (наборів) аргументів Х визначається за формулою:
С = 2n; де: С – число комбінацій,
n – число вхідних змінних (аргументів, складових). Для двох доданків Х1 і Х2 при С = 4 таблиця істинності виглядає так.
Таблиця 1
| Х1 | Х2 | Y = Х1 + Х2 |
З таблиці видно, що результат Y = 0 буде тільки в одному випадку: при Х1 = Х2 = 0.
Практично реалізувати операції логічного складання може електрична схема, яка показана на мал. 1.
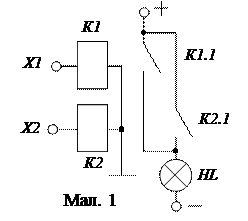 На вхід схеми (на обмотки електромагнітних реле) поступають незалежні один від одного сигнали XI і Х2. Наявність напруги на вході відповідає логічній «1», а його відсутність – логічному «0». Кожне реле має робочий контакт, який замкнутий за наявності струму в обмотці і розімкнений за відсутності його. Такі контакти називають нормально розімкненими. Операцію логічного складання сигналів Х1 і Х2 здійснює електричне коло, яке складається з джерела напруги і навантаження Л, яке замикається через паралельно включені контакти реле (К1 і, К2). Дійсно, за наявності хоча б одного з сигналів Х (тобто коли замкнеться хоча б один з ключів К) коло сигналу Y замкнеться (Y = 1) і лампочка HL зажевріє. При Х1 = 0 і Х2 = 0 контакти К1 і К2 будуть розімкнені і, отже, лампочка горіти не буде (Y = 0).
На вхід схеми (на обмотки електромагнітних реле) поступають незалежні один від одного сигнали XI і Х2. Наявність напруги на вході відповідає логічній «1», а його відсутність – логічному «0». Кожне реле має робочий контакт, який замкнутий за наявності струму в обмотці і розімкнений за відсутності його. Такі контакти називають нормально розімкненими. Операцію логічного складання сигналів Х1 і Х2 здійснює електричне коло, яке складається з джерела напруги і навантаження Л, яке замикається через паралельно включені контакти реле (К1 і, К2). Дійсно, за наявності хоча б одного з сигналів Х (тобто коли замкнеться хоча б один з ключів К) коло сигналу Y замкнеться (Y = 1) і лампочка HL зажевріє. При Х1 = 0 і Х2 = 0 контакти К1 і К2 будуть розімкнені і, отже, лампочка горіти не буде (Y = 0).
Логічне множення (кон’юнкція)
При логічному множенні вхідні змінні (число співмножників може бути будь-яким) з’єднуються сполучником «І» і позначають символом «Ù» або знаком множення (·) і записується вона у вигляді:
Y = Х1 Ù Х2
або:
Y = Х1·Х2.
Запис читається таким чином: Y дорівнює XI І Х2. Така функція Y = Х1·Х2
| Х1 | Х2 | Y = Х1·Х2 |
Таблиця 2
приймає значення логічної «1» тільки при рівності одиниці всіх вхіднихзмінних (Х1=Х2 = 1). Якщо хоч одна змінна буде рівна 0, то і вихідна функція теж буде рівна нулю. Таблиця істинності для кон’юнкції має вигляд:
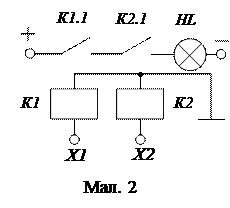 Розглянемо електричну схему, що виконує операцію логічного множення. Схема побудована на електромагнітних реле, контакти яких включені, на відміну від схеми, приведеної на мал. 1, не паралельно, а послідовно. Лампочка HL в колі сигналу Y зажевріє тільки тоді, коли всі контакти (К1 і К1) будуть замкнуті, тобто при одночасному спрацьовуванні всіх реле (Х1=1 і Х2 = 1) (мал. 2).
Розглянемо електричну схему, що виконує операцію логічного множення. Схема побудована на електромагнітних реле, контакти яких включені, на відміну від схеми, приведеної на мал. 1, не паралельно, а послідовно. Лампочка HL в колі сигналу Y зажевріє тільки тоді, коли всі контакти (К1 і К1) будуть замкнуті, тобто при одночасному спрацьовуванні всіх реле (Х1=1 і Х2 = 1) (мал. 2).
Логічне заперечення (інверсія)
При логічному запереченні (функція «НЕ») значення вихідної функції протилежне вхідній змінній. Операція записується у вигляді:
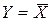
і читається: Y дорівнює не Х. Цезначить, що Y істинно, якщо Х хибне (Х = 0) і навпаки.
Таблиця 3
| Х | Y |
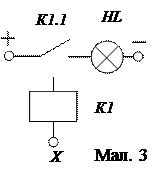 Операція логічного заперечення може бути реалізована на одному електромагнітному реле (мал. 3), що має нормально замкнуті контакти (контакти на розмикання), тобто за відсутності сигналу Х (Х =0) коло замкнуто, про що свідчитиме лампочка, що світиться, але коли на вхід X буде поданий сигнал (Х =1) – коло розімкнеться і лампочка потухне.
Операція логічного заперечення може бути реалізована на одному електромагнітному реле (мал. 3), що має нормально замкнуті контакти (контакти на розмикання), тобто за відсутності сигналу Х (Х =0) коло замкнуто, про що свідчитиме лампочка, що світиться, але коли на вхід X буде поданий сигнал (Х =1) – коло розімкнеться і лампочка потухне.
Схемна реалізація різних функцій дозволяє створювати різні функціональні елементи, на яких побудована сучасна електронно-обчислювальна техніка.
При схемній реалізації ставиться вимога – задіювати якомога менше число елементів, що входять в схему. Щоб це здійснити, треба:
1. перекласти задачу, поставлену перед конструктором, на мову алгебри логіки (задача представляється у вигляді складного вислову, функції перемикача, що описує той або інший функціональний вузол);
2. мінімізувати даний складний вислів, тобто провести тотожні перетворення, які дозволять спростити запис функції перемикача, а, отже, і практично її реалізувати;
3. за спрощеним записом виробити схемну реалізацію поставленої задачі.
При мінімізації логічних функцій використовують наступну основну тотожність і закони алгебри логіки.
Все це властивості операцій «+» і «·»:
Таблиця 4
| для диз’юнкції | для кон’юнкції | |

| 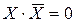
| |
| Х + Х = Х | Х · Х = Х | |
| Х + 1 = 1 | Х · 1 = Х | |
| Х + Х = Х | Х · 0 = 0 | |
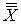 = Х = Х
|
Пересувний закон:
Х1 + Х2 = Х2 + Х1; Х1 · Х2 = Х2 · Х1.
Сполучний закон:
(Х1 + Х2) + Х3 = Х1 + (Х2 + Х 3); (Х1 · Х2) · Х3 = Х1 · (Х2 · Х3).
Розподільний закон:
– операції «+» відносно «·»:
Х · (Y + Z) = Х · Y + Х · Z;
– операції «·» відносно «+»:
Х + (Y · Z) = (Х + Y) · (Х + Z);
У останньої формули не зовсім звичний вигляд, але користуюся вказаною вище вказаною тотожністю, можна довести справедливість цієї рівності і сформулювати наступне правило: щоб виконати операцію з комплексом, треба виконати її з кожним учасником комплексу і результати об’єднати операцією комплексу.
Для мінімізації логічних функцій перемикачів користуються ще такими формулами:
– формула поглинання: X + X · Y = X,
– формула склеювання: X · Y + X ··  = X.
= X.
Важливе значення при тотожних перетвореннях має співвідношення подвійності (теореми де Моргана):
 ,
,
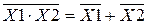 .
.
Це допомагають взаємно замінювати операції диз’юнкції і кон’юнкції, а це дає можливість побудувати будь-яку логічну функцію, використовуючи тільки дві операції «І» та «НЕ» або «АБО» і «НЕ».
Перевірити справедливість всіх виразів можна за допомогою таблиць істинності.
Двійкова система числення
В аналоговій техніці існує ряд властивих їй недоліків: інформаційні спотворення при передачі, які не підлягаючі виправленню, складність запам’ятовування і невисока точність. Ці недоліки примусили звернутися до нової форми представлення інформації – цифровий.
У цифровій техніці безперервні повідомлення, інформація представляється в дискретній формі. Кожне значення дискретного сигналу можна представити числом. У цифровій техніці такий процес називається кодуванням, а сукупність одержаних чисел – кодом сигналу. Таким чином, дискретне повідомлення складається з набору чисел і символів (наприклад, знаків «+» «–»). Кожне слово складається з цифр. Спосіб запису чисел цифровими знаками називається системою числення. У цифровій техніці використовуються так звані позиційні системи числення. Значення кожної цифри, що входить у склад числа, залежить від її положення у записаному числі. Кількість різних цифр, що вживаються у позиційній системі, називають основою системи. У цифровій техніці найбільшого поширення набула двійкова система числення, що містить тільки цифри 0 і 1, а її основою служить число 2. Наприклад, число 25 в десятковій і двійковій системах може бути представлено у вигляді:
2510 = 2·101 + 5·100 = 1·24 + 1·23 + 0·22 + 0·21 + 1·20.
Іноді використовують вісімкову і шістнадцяткову системи. Їх, зокрема, застосовують при складанні програм для зручнішого і коротшого запису двійкових кодів команд, оскільки ці системи не вимагають спеціальних операцій для перекладу в двійкову систему.
Числа десяткової системи числення неважко перевести у числа двійкової системи. Щоб перевести ціле число з основою 10 в систему з основою 2, необхідно послідовно ділити задане число на 2 і число, що було одержано в процесі поділу – частка, знов ділиться на 2 до тих пір, поки остання частка не виявиться менше 2. Результат переводу записують у вигляді послідовності цифр зліва направо, починаючи з останньої частки і кінчаючи першим залишком (при цьому цифра молодшого розряду є перший залишок). Всі дії в процесі ділення числа виконують в десятковій системі.
Перехід від двійкового запису до десяткового виконується порозрядним підсумовуванням.
Правила виконання арифметичних дій над двійковими числами задаються табл. 5.
Таблиця 5
| Двійкове складання | Двійкове віднімання | Двійкове множення |
| 0 + 0 = 0 | 0 – 0 = 0 | 0 · 0 = 0 |
| 0 + 1 = 1 | 1 – 0 = 1 | 0 · 1 = 0 |
| 1 + 0 = 1 | 1 – 1 = 0 | 1 · 0 = 0 |
| 1 + 1 = 10 | 10 – 1 = 1 | 1 · 1 = 1 |
Логічні елементи
Всі математичні і логічні перетворення, які відбуваються з інформацією, здійснюються електронними першоцеглинками – логічними елементами.
Логічний елемент – це електрична схема, електронний пристрій, що реалізує одну з логічних функцій. На принциповій схемі логічний елемент зображають прямокутником, всередині якого відповідним значком вказується функція, яку він здійснює. Лінії з лівого боку прямокутника показують входи, а з правого – виходи елементу.
Основних логічних елементів, використовуваних в пристроях, три:
– елемент «АБО»,
– елемент «І»,
– елемент «НЕ»,
Елемент «АБО» (диз’юнктор)
Елемент «АБО» виконує операцію логічного складання:
У = X1 + X2.
 На мал. 4 показане умовне графічне позначення диз’юнктора. Число входів Х у нього може бути два і більше. Сигнали «0» і «1» (низького і високого рівня різко відрізняються за значенням напруги і не можуть бути сплутані між собою. Для мікросхем ТТЛ серій сигнал «1» повинен мати напругу U 1 = 2,4 … 5 В, а сигнал «0» – U 0 = 0 … 0,4 В. Для мікросхем КМОП-структур:
На мал. 4 показане умовне графічне позначення диз’юнктора. Число входів Х у нього може бути два і більше. Сигнали «0» і «1» (низького і високого рівня різко відрізняються за значенням напруги і не можуть бути сплутані між собою. Для мікросхем ТТЛ серій сигнал «1» повинен мати напругу U 1 = 2,4 … 5 В, а сигнал «0» – U 0 = 0 … 0,4 В. Для мікросхем КМОП-структур:
U 1 = 0,7U живл ;
U 0 = 0,3U живл.
Сигнал «1» з’явиться на виході Y, якщо на будь-якому одному або декількох входах присутній «1»; сигнал «0» – тільки у тому випадку, коли на всі входи X поступає сигнал «0».
Елемент «І» (кон’юнктор)
Елемент «І» виконує операцію логічного множення:
Y = X1 · X2.
 Кількість входів X може бути будь-яким (від двох і більш). У цьому елементі на виході Y з’являється логічна «1» тільки у тому випадку, коли на всі входи X подається сигнал «1». За наявності логічного «0» хоча б на одному з входів на виході буде сигнал «0».
Кількість входів X може бути будь-яким (від двох і більш). У цьому елементі на виході Y з’являється логічна «1» тільки у тому випадку, коли на всі входи X подається сигнал «1». За наявності логічного «0» хоча б на одному з входів на виході буде сигнал «0».
Умовне графічне позначення кон’юнктора виконане на мал. 5.
Елемент «НЕ» (інвертор)
Елемент не виконує операцію логічного заперечення:
 .
.
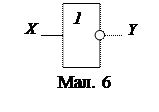 Він має лише один вхід. Сигнал «1» на виході Y з’явиться у разі, коли на вхід Х поступає сигнал «0»; коли ж на вхід Х поступає «1», з виходу Y знімається сигнал «0».
Він має лише один вхід. Сигнал «1» на виході Y з’явиться у разі, коли на вхід Х поступає сигнал «0»; коли ж на вхід Х поступає «1», з виходу Y знімається сигнал «0».
На мал. 6 показане умовне графічне позначення інвертування.
На початку були розглянуті електричні схеми, що виконують логічні операції, на електромагнітних реле. Ці ж функції виконують логічні елементи. Наведемо приклади реалізації логічних схем на електронних елементах (мал. 7).
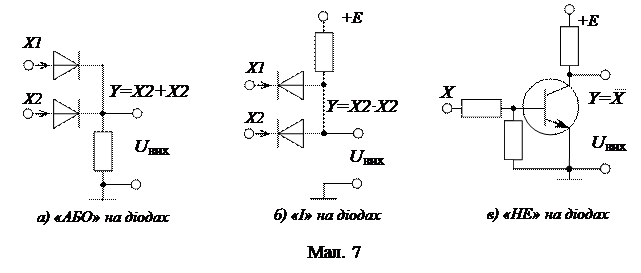 |
Використовуючи ці три основні логічні елементи, можна побудувати безліч логічних пристроїв, що виконують будь-які складні перетворення. Ці перетворення є комбінаціями простих логічних операцій. Розглянемо лише два з них, які є універсальними, оскільки, маючи тільки ці елементи, можна побудувати будь-який логічний пристрій. Це елементи «І-НЕ» і «АБО-НЕ».
Елемент «І-НЕ»
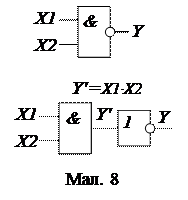 Цей елемент реалізує функцію:
Цей елемент реалізує функцію:
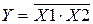 – інверсію добутку.
– інверсію добутку.
Він складається з елементів «И» і «НЕ», сполучених послідовно між собою (мал. 8).
Працює елемент таким чином. Якщо хоча б на одному з входів X немає сигналу «1», то в результаті логічного множення X1 · X2 на виході Y’ повинен був з’явитися сигнал «0», але вихід Y’ інвертований, отже, на виході матимемо в цьому випадку «1». Коли ж на всі входи X поступить «1», на попередньому виході Y’ буде «1», а на інвертованому виході Y – «0».
Таким чином, елемент «І–НЕ» видає «1» за наявності «0» хоча б на одному із входів X і лише під час подання «1» на всі входи на виході з’явиться «0».
Цьому елементу, згідно теореми до Моргана
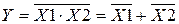 ,
,
буде еквівалентний елемент «НЕ–АБО», який здійснює функцію

 – суму інверсій (див. мал. 9).
– суму інверсій (див. мал. 9).
Отже, в схемах може бути здійснена заміна елементу І-НЕ на елемент АБО з інвертованими на входах сигналами.
Елемент АБО – НЕ (елемент Пірса)
 Елемент реалізує функцію
Елемент реалізує функцію 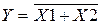 (інверсія суми). Він складається з послідовно сполучених двох основних елементів «АБО» і «НЕ» (мал. 10).
(інверсія суми). Він складається з послідовно сполучених двох основних елементів «АБО» і «НЕ» (мал. 10).
Працює елемент таким чином. За наявності «1» хоча б на одному або всіх входах Х на виході Y’ буде « 1», а на остаточному виході Y – «0», лише тільки тоді, коли на всі входи Х поступатиме «0», на виході Y’ матимемо «0», а на виході Y – «1».
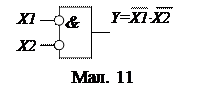 Таким чином, елемент видає на виході «1» тільки в тому випадку, якщо на всі входи Х поступає «0»; у решті випадків на виході Y буде «0».
Таким чином, елемент видає на виході «1» тільки в тому випадку, якщо на всі входи Х поступає «0»; у решті випадків на виході Y буде «0».
Тотожний елементу Пірсу АБО-НЕ буде елемент НЕ-І, що виконує логічний добуток інвертованих сигналів (мал. 11).
Число входів в логічних елементах різного призначення може бути будь-яким, але всі входи кожного елементу рівнозначні. Деякі з них при роботі в конкретних пристроях не використовуватися. Невживані входи в схемах І, І-НЕ сполучають з + U живл, а в схемах АБО, АБО-НЕ, складання по модулю 2 – із загальним провідником.
Тригери
Однією з чудових властивостей цифрової інформації є те, що можливо побудувати для неї статичні пристрої, що запам’ятовують. Простими цифровими пристроями для запам’ятовування є тригери.
Тригер – це пристрій послідовного типу з двома стійкими станами рівноваги, призначене для запису і зберігання інформації. Під дією вхідних сигналів тригер може перемикатися з одного стійкого стану в інший. При цьому напружено на його виходах змінюється стрибкоподібно.
Грубою механічною моделлю тригера може служити перекидна дошка – гойдалка, яку можна побачити на будь-якому дитячому майданчику. Така дошка за відсутності зовнішньої дії знаходиться в одному з двох стійких станів, при якому один з її кінців упирається в землю.
Два стійкі стани тригера називають одиничними і нульовими.
Тригер в загальному випадку має один або декілька входів, на які поступають керуючі сигнали, і два виходи: прямий Q, або одиничний, і інверсний 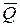 – зворотний, або нульовий. В одиничному стані тригера на виході Q підтримується рівень логічної «1», а на виході
– зворотний, або нульовий. В одиничному стані тригера на виході Q підтримується рівень логічної «1», а на виході 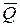 – рівень логічного «0»; у нульовому стані – навпаки.
– рівень логічного «0»; у нульовому стані – навпаки.
Найважливішою характеристикою тригера є його швидкодія, тобто здатність переходити з одного стійкого стану в інший за короткий час Чисельно швидкодія визначається як максимально допустиме число перемикань за одиницю часу. Час, необхідний для приведення схеми в рівновагу після чергового стрибка, тобто мінімальний допустимий час між двома перемиканнями, називається роздільним часом тригера
За способом запису інформація тригери діляться на асинхронні і синхронізуються (тактовані).
У асинхронних тригерах інформація може записуватися безперервно і визначається інформаційними сигналами, що діють на входах у даний момент часу. Якщо інформація заноситься в тригер тільки у момент так званого синхронізуючого сигналу, то такий тригер називається таким, що синхронізується або тактованим. Крім інформаційних входів, тригери, що синхронізуються, мають тактовий вхід (вхід синхронізації).
У цифровій техніці прийняті наступні позначення входів тригерів:
S – роздільний вхід установки в одиничний стан (напруга високого рівня на прямому виході Q);
R – роздільний вхід установки в нульовий стан (напруга низького рівня на прямому виході 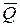 );
);
D – інформаційний вхід (на нього подається інформація, призначена для занесення в тригер);
С – вхід синхронізації;
Т – рахунковий вхід.
У логічних пристроях використовують різні типи тригерів на різноманітній елементній базі. Найбільшого поширення з них набули RS -тригери з двома настановними входами, тактований D-тригер і рахунковий Т-тригер.
Розглянемо функціональні можливості кожного з них.
Асинхронний RS-тригер
RS-тригер має два настановні входи: R – вхід встановлення в «0» стан і – в «1» стан.
Залежно від логічної структури RS-тригери можуть бути або з прямими входами – керуються «одиницями», або з інверсними входами – керуються «нулями». На малюнках 12 і 13 наведені їх схеми і умовні графічні зображення.
Такі тригери побудовані на двох логічних елементах:
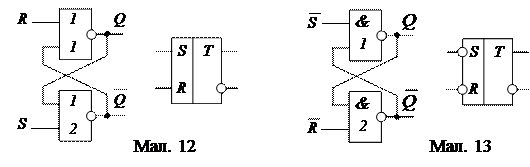 |
2АБО-НЕ – тригер з прямими входами (див. мал. 12) і
2І-НЕ – тригер з інверсними входами (див. мал. 13).
 |
З схем видно, що вихід кожного з елементів підключений до одного з входів іншого елементу, тобто створений глибокий позитивний зворотний зв’язок, який забезпечує тригеру два стійкі стани.
Як же працюють такі тригери?
Розглянемо тригер, побудований не основі 2-х елементів Пірса (АБО-НЕ).
Хай на вхід S поступає сигнал «1», а на вхід R – «0», тоді згідно роботі елементу АБО-НЕ (якщо хоча б на одному з входів комірки 2 є сигнал «1» то на Y (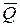 )буде завжди – «0», тобто тригер знаходитиметься в стані «1» (див. мал. 14).
)буде завжди – «0», тобто тригер знаходитиметься в стані «1» (див. мал. 14).
Якщо поміняти сигнали на тому ж вході S з «0» на «1», то стан комірки 2 не зміниться і, отже, тригер залишиться в стані «1», (графічне пояснення див. на мал. 15).
Тепер замінимо сигнал на вході R з «0» на «1» а на S залишиться сигнал останнього випадку, що розглядався, – «0» то на виході з’явиться «0» і, за збігом «0» на входах комірки 2, на виході 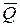 з’явиться «1», тобто тригер перейде в стан «0». В даному випадку зміна сигналу на вході R на протилежний (з «1» на «0») не спричинить за собою зміни стану тригера і він, як і раніше, знаходитиметься в стані «0» (див. мал. 16).
з’явиться «1», тобто тригер перейде в стан «0». В даному випадку зміна сигналу на вході R на протилежний (з «1» на «0») не спричинить за собою зміни стану тригера і він, як і раніше, знаходитиметься в стані «0» (див. мал. 16).
 |
Якщо на входи R і S подати сигнали «1», то на обох виходах одержимо «0», але в такому стані схема не є тригером, т. я, згідно його визначенню, повинен знаходитися в одному з протилежних станів. Така ситуація не є небезпечною для тригера, але все таки, щоб цього не було у нього, на даний випадок існує захист.
Легше і швидше зрозуміти роботу такого тригера можна за допомогою таблиці істинності 6, де Qt і 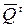 позначать рівні, які були на виходах тригера до подачі на його входи інформаційних сигналів (так званих активних рівнів). Активним називає логічний рівень, який діє на вході логічного елементу і однозначно визначає логічний рівень вихідного сигналу – стан тригера (незалежно від логічних рівнів, що діють на решті входів); Qt+1 і
позначать рівні, які були на виходах тригера до подачі на його входи інформаційних сигналів (так званих активних рівнів). Активним називає логічний рівень, який діє на вході логічного елементу і однозначно визначає логічний рівень вихідного сигналу – стан тригера (незалежно від логічних рівнів, що діють на решті входів); Qt+1 і 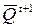 – логічні рівні на виходах тригера після подачі інформації на його входи.
– логічні рівні на виходах тригера після подачі інформації на його входи.
Таблиця 6
| S | R | Qt | 
| Qt+1 | 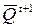
|
| * | * | ||||
| * | * |
Висновок: таким чином, для тригера з прямими входами сигнал «0» є пасивним, оскільки наявність його на вході не визначає однозначно стан схеми, а сигнал «1» є, безумовно, активним. За наявності «1» на вході S на прямому виході обов’язково буде «1», а за наявності «1» на R – на виході Q буде «0». Отже, тригер управляється сигналом рівня «1».
Допустимі для нього поєднання сигналів:
1. S = 1, R = 0 (Qt+1 = 1, 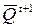 = 0, тригер в стані «1»);
= 0, тригер в стані «1»);
2. S = 0, R = 1 (Qt+1 = 0, 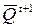 = 1, тригер в стані «0»);
= 1, тригер в стані «0»);
3. S = 0, R =0 (тригер утримує попередній стан);
При S = R = 1 стан тригера буде невизначеним, оскільки під час дії інформаційних сигналів логічні рівні на виходах тригера однакові (Q t +1 = 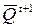 = 0), а після закінчення їх дії тригер може рівноімовірно прийняти будь-який із стійких станів. Тому така комбінація сигналів є забороненою.
= 0), а після закінчення їх дії тригер може рівноімовірно прийняти будь-який із стійких станів. Тому така комбінація сигналів є забороненою.
Режим S = 1, R = 0 називають режимом запису «1» (оскільки Qt+1 = 0); режим S = 0, R = 1 – режим запису «0». Режим S = 0, R = 0 називають режимом зберігання інформації, оскільки інформація на виході залишається незмінною
Для тригера з інверсними входами сигнал «1» є пасивним, а сигнал «0» – активним, оскільки за наявності «0» хоча б на одному з входів, відповідно, на якомусь одному з виходів обов’язково буде «1». Отже, цей тригер управляється сигналами «0». Для нього таблиця 7 істинності має вигляд:
Таблиця 7
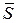
| 
| Qt | 
| Qt+1 | 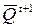
|
| * | * | ||||
| * | * | ||||
Режим запису логічної «1» в такому тригері реалізується, як видно з таблиці істинності, при 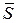 = 0,
= 0,  = 1; режим запису логічного «0» – при
= 1; режим запису логічного «0» – при 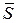 = 1,
= 1,  = 0. При
= 0. При 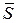 =
=  = 1 забезпечується зберігання інформації. Комбінація
= 1 забезпечується зберігання інформації. Комбінація 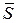 =
=  = 0 є забороненою.
= 0 є забороненою.
Тактований D -тригер
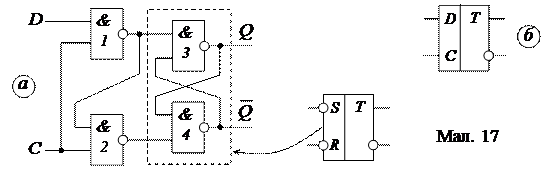 |
Цей тип тригера належить до синхронних. Простий тригер має два робочі входи: інформаційний (D) і тактуючий, на який в певні моменти подають тактуючі імпульси рівня «1». Одна з можливих структурних схем однотактного D -тригера і його умовне позначення показане на мал. 17.
По інформаційному входу тригера його можна встановити в «0»-й стан сигналом «0» і в стан «1» сигналом «1». Проте спрацьовування тригера по входу D відбувається тільки в ті моменти, коли на вхід С поступає тактуючий імпульс рівня «1». Завдяки цьому забезпечується затримка запису на той або інший відрізок часу.
Розглянемо роботу D -тригера по схемі, складеній з тригера типу 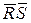 з інвертованими входами і двох елементів І-НЕ – елементів Шеффера.
з інвертованими входами і двох елементів І-НЕ – елементів Шеффера.
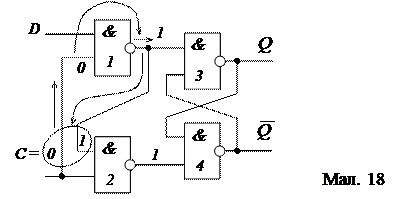 |
Якщо рівень сигналу на вході С = 0, то при цьому з виходів елементів 1 і 2 (незалежно від рівня сигналу на інформаційному вході) на входи
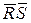 -триггера поступають «1». Це режим зберігання інформації, при якому тригер утримує попередній стан (мал. 18).
-триггера поступають «1». Це режим зберігання інформації, при якому тригер утримує попередній стан (мал. 18).
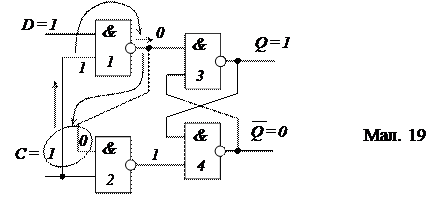
При подачі на вхід синхронізації тактуючого сигналу С = 0 інформація на прямому вході буде повторять інформацію, що подається на вхід D. Якщо, наприклад, у момент надходження тактового імпульсу на вході D буде «1», то по збігу «1» на елементі 1 на вхід  тригера поступає «0», на вхід елементу 2 з виходу елементу 1 подається «0», отже, на вхід тригера
тригера поступає «0», на вхід елементу 2 з виходу елементу 1 подається «0», отже, на вхід тригера  поступає «1». Таким чином, створюється набір сигналів для перекидання тригера в стан «1» або утримання його в цьому стані (Q = 1,
поступає «1». Таким чином, створюється набір сигналів для перекидання тригера в стан «1» або утримання його в цьому стані (Q = 1,  = 0, див. мал. 19).
= 0, див. мал. 19).
 |
Якщо ж у момент надходження тактуючого сигналу на вході D є сигнал «0», то по збігу «1» на входах елементу 2 на вхід
 тригера подається «0», а з елементу 1
тригера подається «0», а з елементу 1 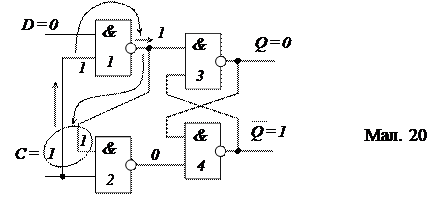 |
поступає «1» на вхід
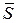 . Таким чином, забезпечується «перекидання» тригера в стан «0» або утримання його в цьому стані (мал. 20)
. Таким чином, забезпечується «перекидання» тригера в стан «0» або утримання його в цьому стані (мал. 20)
Таблиця 8 істинності тактованого D-тригера має вигляд:
Таблиця 8
| D | Qt | Qt+1 |
де: Qt – логічний рівень на прямому виході до подачі імпульсу синхронізації;
Qt+1 – логічний рівень на цьому ж виході після подачі імпульсу синхронізації.
 |
Висновок: таким чином, при С = 0 Qt+1 = Qt, при С = 1 Qt+1 = D.
На мал. 21 зображені часові діаграми тактованого D- тригера. Як вже було сказано, на такому тригері відбувається затримка сигналу на виході по відношенню до сигналу, поданого на вхід, на час паузи між синхросигналами. Для стійкої роботи тригера необхідно, щоб протягом синхроімпульса інформація на вході була незмінною.
Тактовані D- тригериможуть бути потенційними і динамічними управлінням. У перших з них інформація записується протягом часу, при якому рівень сигналу С = 1. У тригерах з динамічним управлінням інформація записується тільки протягом перепаду напруги на вході синхронізації. Динамічні входи зображаються на схемі трикутником. Якщо вершина трикутника обернута у бік мікросхеми, то тригер спрацьовує по фронту вхідного імпульсу, а якщо від неї – по зрізу імпульсу. У такому тригері інформація на виході може бути затримана на один такт по відношенню до вхідної інформації.
Рахунковий Т-тригер
Простий Т -тригер має тільки один управляючий вхід Т і два виходи: Q і 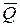 . Інформація на виході такого тригера міняє свій рівень на протилежний при кожному позитивному (або негативному перепаді напруги на вході, тобто під час вступу на вхід командного сигналу тригер міняє своє стан, при зміні командного сигналу на зворотний стан тригера не міняється. Таким чином, Т- тригер « рахує» поступаючі на нього імпульси, змінюючи свій стан з приходом кожного з них. Тому Т- тригерназивають рахунковим.
. Інформація на виході такого тригера міняє свій рівень на протилежний при кожному позитивному (або негативному перепаді напруги на вході, тобто під час вступу на вхід командного сигналу тригер міняє своє стан, при зміні командного сигналу на зворотний стан тригера не міняється. Таким чином, Т- тригер « рахує» поступаючі на нього імпульси, змінюючи свій стан з приходом кожного з них. Тому Т- тригерназивають рахунковим.
Умовне графічне позначення рахункового тригера, дано на мал. 22а.
 |
У серіях мікросхем Т -тригерів, що випускаються, як правило, ні. Але тригер такого типу може бути створений на базі тактованого динамічного D- тригера, якщо його інверсний вихід з’єднати з інформаційним входом (мал. 22б). Функцію рахункового входу виконує тактуючий вхід С.
Хай спочатку тригер знаходиться в стані «1», тобто на виході Q буде «1», а на 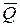 – «0». Отже, на його вхід D подається сигнал рівня «0». Поки на вході С є «0», тригер зберігатиме свій первинний стан. Але з приходом тактуючого імпульсу відбувається наступне: На прямому виході Q з’являється «0», а стан виходу
– «0». Отже, на його вхід D подається сигнал рівня «0». Поки на вході С є «0», тригер зберігатиме свій первинний стан. Але з приходом тактуючого імпульсу відбувається наступне: На прямому виході Q з’являється «0», а стан виходу 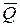 завжди протилежно стану тригера – «1». Цей рівень записуватиметься і при зміні сигналу на С на протилежний; С = 0, на інформаційний вхід при цьому посилатиметься «1». З приходом нового (чергового) імпульсу на тактований вхід тригер «перекидатиметься» в «0» стан і т.д.
завжди протилежно стану тригера – «1». Цей рівень записуватиметься і при зміні сигналу на С на протилежний; С = 0, на інформаційний вхід при цьому посилатиметься «1». З приходом нового (чергового) імпульсу на тактований вхід тригер «перекидатиметься» в «0» стан і т.д.
 |
Зміна стану такого тригера відповідає моменту надходження на вхід початку (переднього фронту) тактуючого сигналу (про що свідчить обернута у бік мікросхеми вершина трикутника на вході С на умовному зображенні тригера), тому тривалість імпульсу на виході
 удвічі більша, ніж на вході, а частота – в два рази менша (див. часову діаграму мал. 22в). Це легко бачити на часових діаграмах вхідного і вихідного сигналів.
удвічі більша, ніж на вході, а частота – в два рази менша (див. часову діаграму мал. 22в). Це легко бачити на часових діаграмах вхідного і вихідного сигналів.
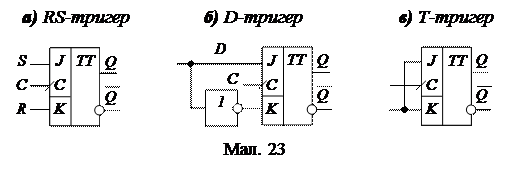
У сучасній апаратурі, елементною базою якої служать інтегральні мікросхеми, широко використовуються універсальні тригери типа JK, які залежно від способу включення входів можуть працювати як RS-, D- або Т- тригери(мал. 23).
Регістр
Регістр – вузол, призначений для прийому і зберігання чисел з двійковим представленням цифр розрядів (кодом чисел).
Основними видами регістрів є паралельні і послідовні (зсовуючі).
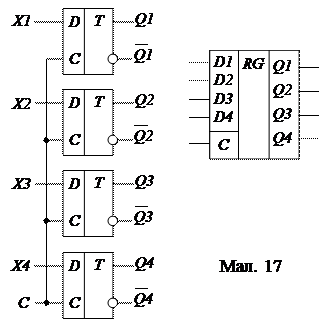 У паралельному регістрі на тактованих D- тригерах ( мал. 24) код числа, що запам’ятовується, подається на інформаційні входи всіх тригерів і записується в регістр з приходом тактового імпульсу. Вихідна інформація, що знімається з Q1 … Q4, змінюється з подачею нового вхідного слова і приходом наступного імпульсу запису.
У паралельному регістрі на тактованих D- тригерах ( мал. 24) код числа, що запам’ятовується, подається на інформаційні входи всіх тригерів і записується в регістр з приходом тактового імпульсу. Вихідна інформація, що знімається з Q1 … Q4, змінюється з подачею нового вхідного слова і приходом наступного імпульсу запису.
Такі регістри використовуються у системах оперативної пам’яті. Число тригерів в них рівне максимальній розрядності слів, що зберігаються.
Послідовний регістр.
У регістрі зсуву запис коду числа здійснюється послідовною передачею двійкових сигналів на тригери відповідних розрядів.
Розглянемо принцип роботи чотирьохрозрядного регістра зсуву на D- тригерахпри записі двійкового числа 1011. Схемі послідовного регістра і часова діаграма, що ілюструє його роботу, приведена на мал. 25.
У початковому стані всі тригери знаходяться в «0». До приходу першої команди на вхід С («зсув») на вхід D першого тригера поступає сигнал коду молодшого розряду – «1». З приходом імпульсу зсуву перший тригер перейде в стан «1», а другий, третій і четвертий залишаться в первинному стані
 |
– «0». За час перерви між імпульсами зсуву на вхід першого тригера поступить кодовий сигнал другого розряду «1». Тому з приходом чергового імпульсу зсуву тригер знов прийме стан «1», що відповідно сигналу на вході «Запис». Другому, одночасно з другим сигналом «Зсув», на інформаційний вхід поступить сигнал «1». Отже, він повторять попередній стан першого (тобто перейде в «1»), а третій і четвертий за рахунок двох попередніх нульових станів першого і другого залишаться в «0».
По черговому сигналу «Зсув» на вхід D першого тригера поступить «0» (код третього розряду), він перейде в стан «1», одночасно з цим 2-й тригер – в стан «1»,, 3-й – в «1».
І по четвертому імпульсу на вхід С, при якому при подачі на D 1-го тригера останнього розряду коду числа – «1», 1-й тригер прийме стан «1», 2-й – попередній стан 1-го – «0», 3-й – «1», 4-й – «1».
Таким чином, по четвертому імпульсу зсуву на виходах тригерів буде записав двійковий код числа 1011 («1» – Q4, («1» – Q3, («0» – Q2, («1» – Q1).
І по четвертому імпульсу на вхід С, при якому при подачі на D 1-го тригера останнього розряду коду числа – «1», 1-й тригер прийме стан «1», 2-й – попередній стан 1-го – «0», 3-й – «1», 4-й – «1».
Кожен тактовий імпульс послідовно зсовує код числа в регістрі на один розряд, тому для запису N -розрядного коду потрібно N тактових імпульсів і тригерів. Записаний двійковий код числа зберігається в регістрі у вигляді паралельного коду на виходах QN – Q1 ( для числа 1011 – Q4 – Q1) до приходу чергового N+1 (5-го) тактового імпульсу. Якщо необхідно одержати інформацію, що зберігається, в послідовному коді, то її знімають з N-го виходу (5-го) у момент приходу наступних N (чотирьох 5 … 9) імпульсів 9N + 1 … 2N + 1).
Лічильники
 |
Лічильником називають пристрій, призначений для підрахунку числа імпульсів, поданих на вхід. Вони, як і зсовуючі регістри, можуть бути представлені у вигляді послідовного ланцюжка тригерів. Найбільш економні і поширеніші лічильники, утворюються рахунковими Т-тригерами (мал. 26).
Після кожного тактового імпульсу Т сигнал на інверсному виході 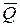 міняється на протилежний і тому частота вихідних імпульсів удвічі менше частоти, що поступають (тригери працюють як дільники частоти на два). Тому, зібравши послідовний ланцюжок з n RST- тригерів(сполучаючи вихід
міняється на протилежний і тому частота вихідних імпульсів удвічі менше частоти, що поступають (тригери працюють як дільники частоти на два). Тому, зібравши послідовний ланцюжок з n RST- тригерів(сполучаючи вихід 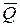 попереднього тригера з рахунковим входом З наступного), одержимо частоту f вих = f вх /2n.
попереднього тригера з рахунковим входом З наступного), одержимо частоту f вих = f вх /2n.
У початковому стані тригери по входу R встановлюються в «0 (всі тригери скинуті в «0»), настановні входи «S» закриваються сигналом «0» (тригери по входах R і S управляються «1»).
Перший тригер, на вхід Т якого поступають рахункові імпульси, спрацьовують по передньому фронту кожного з них. Він знаходиться в стані «1» при непарному числі імпульсів, що поступають, і в стані «0» при парному. Другий тригер працює в два рази рідше, тобто з надходженням на. вхід схеми кожного другого імпульсу. Він знаходиться у стані «1», якщо число пар імпульсів, що поступили, непарне, і в стані «0», якщо воно парне. Аналогічно, третій тригер «рахує» четвірки, а четвертий – вісімки імпульсів. Найчіткіше представити картину роботи двійкового лічильника дозволяє
 |
часова діаграма цього процесу (мал. 27).
Приклад. Якщо на вхід схеми поступило 13 імпульсів, то перший тригер буде в стані «1» (непарне число імпульсів – 13), другий – в стані «0» (парне число двійок – 6), третій – в стані «1» (непарне число четвірок – 3), четвертий – в стані «1» (непарне число вісімок – 1). Записавши положення тригерів справа наліво, одержимо 1101– двійковий запис числа 13.
Такий лічильник працює з коефіцієнтом рахунку К (модулем), що кратний цілому ступеню 2, і в ньому здійснюється циклічний, перебір К = 2 стійких станів. Розрядність лічильника, а отже, число тригерів визначається максимальним числом, до якого він рахує. Чотирьохрозрядний лічильник може злічити до 15 імпульсів, по 16-му імпульсу його тригери виявляться в стані «0» і рахунок почнеться спочатку. Очевидно, з додаванням наступного 9-того) розряду лічильник може здійснити рахунок до двійкового числа 111112 = 3110 і т. д.
Часто потрібні лічильники з числом стійких станів, відмінних від 2n. Наприклад, в електронному годиннику є мікросхеми з коефіцієнтом рахунку 6 (десятки хвилин), 10 (одиниці хвилин), 7 (дні тижня), 24 (годинник). Для побудови лічильника з модулем К ≠ 2 n можна використовувати пристрій з n тригерів, для якого виконується умова 2 n > К. Очевидно, такий лічильник може мати зайві стійкі стани (2 n – К) Виключити ці непотрібні стани можна використовуванням зворотних зв’язків, по колах яких лічильник перемикається в нульовий стан в тому такті роботи, коли він долічує до числа К. Наприклад, для лічильника з К = 10 потрібні чотири тригери (23 < 10 < 24). Лічильник повинен мати 10 стійких станів N = 0, 1,..., 8, 9. У тому такті, коли він повинен був би перейти в 11-й стійкий стан, його необхідно скинути в початковий нульовий стан.
Суматор
Суматором називається пристрій, що виконує операцію складання чисел в двійковій або десятковій системі. З принципу складання багаторозрядних двійкових чисел виходить, що в кожному i-м розряді знаходиться сума трьох чисел по модулю 2 (доданків А, В і роль третього доданку грає перенесення Рi, що поступило з молодшого розряду) і формує сигнал перенесення в старший розряд Рi+1.
Оскільки доданків 3, то число можливих комбінацій вхідних сигналів 23 = 8. Для прикладу розглянемо і проаналізуємо таблицю істинності однорозрядного суматора (див. табл. 9). За допомогою таблиці запишемо логічний вираз для вихідних величин S і Рi+1 в тих випадках, коли S = 1 і Рi+1 =1.
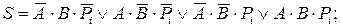
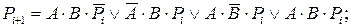
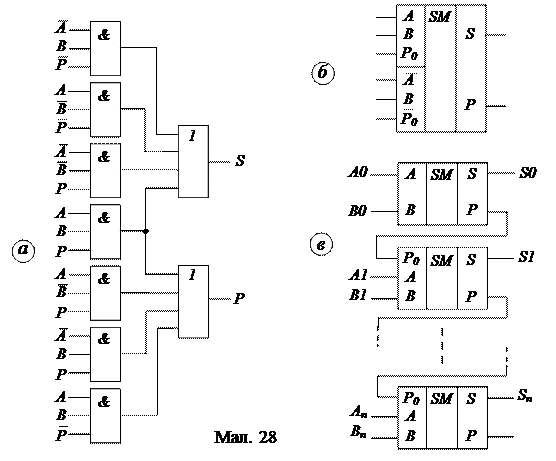 |
За цими функціями можна побудувати суматор на елементах І і АБО (мал. 28а). Умовне позначення однорозрядного суматора приведене на мал. 28б.
Таблиця 9
| Вхід | Вихід | |||
| Доданок | Перенос | Сума | Перенос | |
| А | У | Рi | S | Рi+1 |
Для складання двох багаторозрядних двійкових чисел використовують багаторозрядні суматори, що є в простому вигляді послідовне з’єднання однорозрядних суматорів (мал. 28в).
Шифратор (кодер)
Шифратором називається пристрій, що перетворює одиночний сигнал у n-розрядний двійковий код.
Найбільше застосування він знаходить в пристроях введення інформації (пультах управління) для перетворення десяткових чисел у двійкову систему числення.
Як побудувати такий шифратор?
Хай на пульті десять клавіш з гравіюванням від 0 до 9. При натисненні будь-якої з них на вхід шифратора подається одиничний сигнал, тобто у шифратора повинні бути відповідно 10 входів (Х0 … Х9). На виході шифратора повинен з’явитися двійковий код цього десяткового числа (Y1, Y2,...). З таблиці перемикань видно, в цьому випадку потрібен перетворювач з десятьма входами, як вже було сказано, і чотирма виходами (див. табл. 10).
Таблиця 10
| Десяткове число | Двійковий код | Десяткове число | Двійковий код | ||||||
| Y8 | Y4 | Y2 | Y1 | Y8 | Y4 | Y2 | Y1 | ||
На виході 20 – Y1 одиниця з’являється при натисненні будь-якої з непарних клавіш: Х1, Х3, Х5, Х7, Х9, тобто або Х1 або Х3 або Х5 або Х7 або Х9. Таким чином, логічний вираз для Y1 матиме вигляд:
Y1 = Х1 Ú Х3 Ú Х5 Ú Х7 Ú Х9.
Аналогічним чином визначимо логічні вирази для виходів 21 – Y2, 22 – Y4, 23 – Y8. Вони мають вигляд:
Y2 = Х2 Ú Х3 Ú Х6 Ú Х7,
Y4 – Х4 Ú Х5 Ú Х6 Ú Х7,
Y8 = Х8 Ú Х9.
Отже, для шифратора знадобляться чотири елементи АБО. Комірка 20 повинен мати 5 входів (цифри 1, 3, 5, 7, 9),
комірки 21 і 22 – чотири входи (цифри 2, 3, 5, 7; 4, 5, 6, 7)
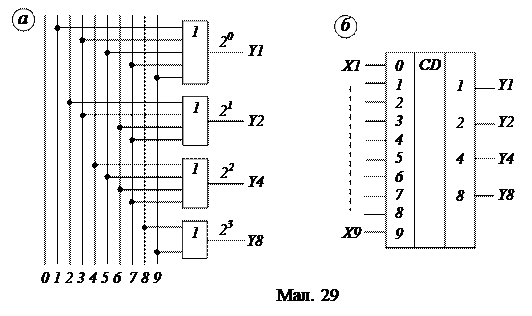 |
і комірка 23 – два входи (цифри 8 і 9). Тоді схема шифратора на елементах АБО виглядатиме таким чином (мал. 29а):
б) умовне графічне (функціональне) позначення шифратора.
Дешифратор (декодер)
 |
Дешифратор – це функціональний вузол, який виконує функцію, зворотну функції шифратора: він перетворює двійковий запис числа, що поступає на його входи, в одиночний сигнал тільки на одному з його виходів. Дешифратори широко застосовуються в пристроях управління, в системах цифрової індикації з газорозрядними цифровими індикаторами і т.д. Наприклад, дешифратор на мікросхемі К155ИД1призначений для роботи з декадними газорозрядними індикаторами. Його виходи підключаються безпосередньо до катодів, що мають форму десяткових цифр. Отже, будь-якому вхідному двійковому коду повинен відповідати низький рівень тільки на одному виході, на всіх інших зберігається високий рівень. Така робота вузла може бути забезпечена за допомогою наступної схеми:
б) умовне графічне позначення дешифратора на мікросхемі К155ИД1
Схема складається з чотирьох входів, на які поступає двійковий код числа, чотирьох інвертувань і 10 чотирьохвходових елементів І-НЕ. На кожен елемент І-НЕ (0 … 9) поступає відповідний набір з 4-х елементів:
Таблиця 11
| Десяткове число | Двійковий код на вході | На входи елементів І-НЕ (набір четвірок) | На виході елементів І-НЕ | ||||||||||||
| Х8 | Х4 | Х2 | Х1 | Y0 | Y1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | Х9 | ||

| |||||||||||||||

| |||||||||||||||

| |||||||||||||||

| |||||||||||||||

| |||||||||||||||
| |||||||||||||||

| |||||||||||||||

| |||||||||||||||
| |||||||||||||||

|






