Переход от А Мура к А Мили
Задан автомат
SA={AA, ZA, WA,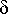 
A, 
A, 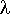a1A},
где
AA = {а1,:, аm,:, aM},
ZA= {z1,:, zf,:, zF},
WA = {w1,:, wg,:, wG};
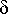A - реализует отображение AA х Z A в AA, 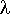A - отображение A A на WA, а a1A = a1 - начальное состояние.
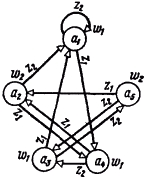
Рис. 1-6. Граф автомата Мура S5
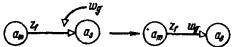
Рис. 1-7. Иллюстрация перехода от модели Мура
к модели Мили
Построим автомат Мили
SB={AB, ZB, W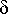B, B, 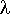B, a1B},
у которого
AB = AA = {а1,:, аm,:, aM},
ZB= ZA = {z1,:, zf,:, zF},
WB = WA = {w1,:, wg,:, wG};
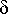B = 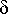A, a1B = a 1A = a1
Функцию выходов Мили 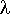B определим следующим образом. Если в автомате Мура 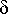A(am,zf)=as и 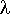A(as)=wg, то в автомате Мили 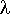B(am,zf)=wg.
Переход от автомата Мура к автомату Мили при графическом способе задания иллюстрируется рис.1-7: выходной сигнал (wg), записанный рядом с вершиной (аs), переносится на все дуги, входящие в эту вершину. На рис. 1-8 приведен граф автомата Мили S6, эквивалентного автомату Мура S3 (рис. 1-4).
При табличном способе задания автомата SA таблица переходов автомата SB совпадает с таблицей переходов SA, а таблица выходов SB получается из таблицы переходов заменой символа as, стоящего на пересечении строки zf и столбца am, символом выходного сигнала wg, отмечающего столбец as, в таблице переходов автомата SA.
Из самого способа построения автомата Мили SB очевидно, что он эквивалентен автомату Мура SA. Действительно, если некоторый водной сигнал zf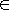 
Z поступает на вход автомата SA, находящегося в состоянии аm, то он перейдет в состояние аs= 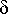A(аm,zf) и выдаст входной сигнал wg= 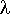A(аs). Но соответствующий автомат Мили SB из состояния am, также перейдет в состояние as, поскольку 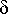B(аm,zf) = 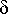A(аm,zf) = аs - и выдаст тот же выходной сигнал wg согласно способу построения функции 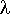В. Таким образом, для входной последовательности длины один поведение автоматов SA и SB полностью совпадает. По индукции нетрудно показать, что любое входное слово конечной длины, поданное на входы автоматов SA и SB , установленных в состояния am, вызовет появление одинаковых выходных слов и, следовательно, автоматы SA и SA аm эквивалентны.
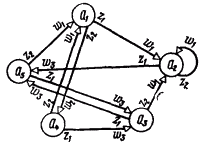
Рис. 1-8. Автомат Мили S6эквивалентный автомату Мура S5
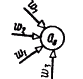
Рис. 1-9. Построение множества As
Переход от А Мили к А Мура
Прежде чем рассмотреть трансформацию автомата-Мили в автомат Мура, наложим на автомат Мили следующее ограничение: у автомата не должно быть преходящих состояний. Под преходящим будем понимать состояние, в которое при представлении автомата в виде графа не входит ни одна дуга, но которое имеет по крайней мере одну выходящую дугу (пример - состояние a1 на рис. 1-3). Итак, пусть задан автомат Мили
SA={AA, ZA, W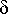A, A, 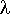A, a1A},
где
AA = {а1,:, аm,:, aM},
ZA= {z1,:, zf,:, zF},
WA = {w1,:, wg,:, wG};
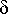A - реализует отображение AA х ZA в AA, 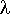A - отображение AA на WA , а a1A = a1 - начальное состояние.
Построим автомат Мура
SB={AB, ZB, W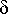B, B, 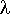B, a1B},
у которого
ZB= ZA = {z1,:, zf,:, zF},
WB = WA = {w1,:, wg,:, wG};
Для определения АB каждому состоянию as 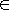AA поставим в соответствие множество As всевозможных пар вида (аs,w g), где wg - выходной сигнал, приписанный входящей в аs дуге (рис. 1-9): Аs={(as, wg) | 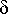(am, zf) = as и 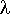(am, zf) = wg}
Число элементов в множестве Аs равно числу различных выходных сигналов на дугах автомата S A, входящих в состояние as.
Множество остояний автомата SB получим как обединение множеств AS (s=1,:,M):
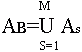
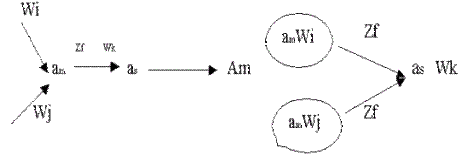
Рис. 1-10. Иллюстрация перехода от модели Мили к модели Мура
Функции выходов 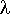B и переходов 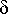B определим слудиющим образом. Каждому состоянию автомата Мура SB, представляющему собой пару вида (as, Wg), поставим в соответствие выходной сигнал Wg. Если в автомате Мили SA был переход а1B (аm, zf) = Wk, то в SB (рис. 1-10) будет переход из множества состояний Am, порождаемых am, в состояние (as, Wk) под действием входного сигнала zf.
В качестве начального состояния а1B можно взять любое из состояний множества А1, которое порождается начальным состоянием а1 автомата SA. Напомним, что при сравнении реакции автоматов SA и SB на всевозможные входные слова не должен учитываться выходной сигнал в момент времени t=0, связанный с состоянием а1B автомата SB .
