Анализ теста по математике в рамках классической теории тестирования
Данный тест по математике состоит из 26 вопросов, разделенных на 3 части: А, В и С (10, 11 и 5 заданий в каждой части соответственно). Части А и В оценивались дихотомически, а часть С – политомически (от 0 до 4). Тест выполнили 1339 учеников. Максимальный балл по тесту составил 36 баллов (из 41 возможного), а минимальный 0 баллов (набрали по 2 человека соответственно). Средний балл за тест составил 13,96 балла. Средний балл по части А - 8,23 (из 10), по В - 4,39 (из 11), по С - 1,34 (из 20).
50% выборки (примерно 670 человек) набрали балл меньше 13. Разброс баллов достаточно большой, подтверждает это не только размах (36 баллов), но и достаточно большое значение стандартного отклонения (6,09). С вероятностью в 95% можно утверждать, что средний балл будет находиться в пределах от 2,02; 25,90. (рис.1. и таблица 1).
Таблица 1 Описательная статистика теста
| Статистика | Значение |
| Среднее | 13,96 |
| Медиана | |
| Стд. отклонение | 6,09 |
| Асимметрия | 0,40 |
| Стд. ошибка асимметрии | ,07 |
| Эксцесс | 0,02 |
| Стд. ошибка эксцесса | ,13 |
| Размах | |
| Минимум | |
| Максимум |
Рис.1. Распределение общего балла за тест
Коэффициент асимметрии положительный и равен 0,4 (распределение смещено вправо), то есть тест более легкий. Эксцесс - положительный (0,02), что говорит об островершинном распределению (однако значение данного коэффициента мало).
Исходя из того, что значения коэффициента асимметрии и эксцесса при нормальном распределении должны находится в пределах 
(где λ вычисляется по функции Лапласа на определенном уровне значимости), при уровне значимости 0,05 (соответствующее значении λ равно 2,25), получаем, что значение коэффициента асимметрии выходит за допустимые пределы (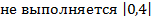
< 0,16), а значение коэффициента эксцесса лежит в необходимых для нормального распределения границах (|0,02| <0,29). В связи с тем, что 2 условия не выполняются одновременно, распределение нельзя считать нормальным.
Надежность теста
Коэффициент надежности теста составил 0,88 (коэф-т Alpha), что говорит о том, что внутренняя согласованность теста достаточно высокая (SEM= 2,08). Данное значение подтверждается значением корреляции между половинами теста при расщеплении пополам по четным/нечетным вопросам (0,81), а также скорректированным коэффициентом корреляции по формуле Спирмена – Брауна (0,90).
Корреляция заданий теста между собой варьируется от 0,03 до 0,5.. Отрицательных корреляций между заданиями теста не было обнаружено, однако ряд коэффициентов корреляции (7 коэффициентов) на уровне значимости 0,05 оказались не значимы, были получены низкие коэффициенты корреляции (таблица 2).
Таблица 2 - Парные коэффициенты корреляции между вопросами
| №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | |
| №24 | ,12** | ,05 | ,12** | ,2** | ,09** | ,17** | ,18** | ,15** | ,13** |
| №25 | ,06* | ,03 | ,06* | ,12** | ,04 | ,08** | ,07* | ,04 | ,06* |
| №26 | ,07** | ,03 | ,07* | ,11** | ,04 | ,09** | ,08** | ,06* | ,05 |
**. Значимая корреляция на уровне значимости 0,01 (2-стороняя значимость)
*. Значимая корреляция на уровне значимости 0,05 (2-стороняя значимость)
- желтым выделены не значимые корреляции, голубым значения коэффициента корреляции < 0,1.
Таким образом, задания 25 и 26 части С очень слабо или совсем не коррелируют со многими заданиями части А, что говорит о том, что возможно цель этих заданий отличалась от целей заданий части А, возможно задания части С были направлены на выявления учеников с особенными знаниями или способностями к математике (например, это задания олимпиадного уровня). Задания части С будут рассмотрены далее подробней.
Трудность и дискриминативность. Часть А и В.
Трудность и дискриминативность дихотомических заданий были посчитаны при помощи программного обеспечения ТАР.
Коэффициент трудности (k) заданий варьируется от 0,13 до 0,98, что говорит о том, что части А и В включают в себя как очень простые, так и сложные задания. Однако, средняя трудность первых двух частей теста составляет 0,6, что говорит о том, что в целом тест обладает хорошим уровнем трудности. Первые 21 заданий теста включают в себя около 8 совсем простых заданий (k>0,75); и 5 очень трудных заданий (k<0,34). Коэффициент трудности остальных заданий находится в пределах от 0,4 до 0,7 (рис.2).
Для оценки дифференцирующей способности задания был рассчитан индекс дискриминативности (рис.2) каждого задания и коэффициент точечной бисериальной корреляции каждого задания с общим баллом за тест (рис.3). Все полученные коэффициенты положительные и находятся в границе от 0,21 до 0,61, что говорит о том, что тест «правильно» дифференцирует учеников на сильных и слабых, и сильные справляются с каждым заданием лучше, чем слабые.
Среднее значение индекса дискриминативности равно 0,5, что говорит о том, что в целом тест хорошо распределяет респондентов на группы. Более подробно можно проанализировать дискриминативность в сочетании с трудностью заданий (рис.2).
Рисунок 2. Показатель трудности и индекс дискриминативности
для частей А и В
Основываясь на индексе дискриминативности, можно выделить два наиболее плохо дифференцирующих задания – 2 и 5. Оба этих задания имеют низкий показатель трудность: задание 2 верно решили 98% испытуемых, задание 5 – 95%. Эти два задания очень простые, с ними справляются почти все ученики, именно поэтому дифференцирующая сила заданий мала.
Хорошей дискриминативностью обладает группа заданий с 10 по 18 (их трудность колеблется в диапазоне от 0,32 до 0,66) и задание 4 (и трудность и дискриминативность =0,63). Сложные задания (19, 20, 21) также имеют достаточно хорошую дискриминативность (0,37; 0,44; 0,32 соответственно).
В целом тест построен по восходящей трудности заданий. Задания части А и В охватывают трудность от 0,98 до 0,13.
Рисунок 3. Корреляция каждого задания с тестовым баллом
*зеленым, желтым и оранжевым отмечены части А, В и С соответственно.
Коэффициенты корреляции заданий ниже 0,3 имеют всего 3 задания (2, 5,25), это свидетельствует о том, что данные задания хуже дифференцируют учеников на «сильных» и «слабых», но в целом, такие значения корреляции можно считать удовлетворительными. Наилучшая корреляция наблюдается у заданий части С – 22 и 23 (0,613), что говорит о хорошем качестве задания. Практически все задания части В имеют высокую корреляцию с тестовым баллом, за исключением задания 19 (0,344), но и данное значение можно считать приемлемым.
Таким образом, в части А и В наиболее низкими показателем дискриминативности обладают задания 2 и 5. Высокий процент правильных ответов на эти задания (высокий показатель трудности) обуславливает низкую дискриминативность. Корреляция с общим баллом так же низкая. Однако, в целом показатели трудности и дискриминативности всего теста и большинства заданий части А и В можно считать хорошими. Задания части С будут рассмотрены нами подробнее в следующем разделе.
Анализ заданий части С.
Задания части С были оценены политомически, поэтому было принято решение проанализировать их отдельно. Для анализа использовалась программа ItemAn v.4.2.1. Задания части С в подобного рода тестах, как правило, самые трудные и выделяют только учащихся с очень высоким уровнем знаний. Для данного теста средняя трудность заданий части С составила 0,27 (очень высокая трудность задания), в то время как для частей А и В средняя трудность – 0,6 (они достаточно простые). Сложность части С стоит учитывать при дальнейшем анализе заданий.
Исходя из базы данных, нами сделано предположение, что за 1 задание части С можно получить от 0 до 4 баллов. Соответственно за полностью решенную часть С можно получить 20 (из 41 возможных за весь тест) баллов, однако средний балл по части С составил 1,94, что опять же подтверждает её экстремальную трудность.
Далее будет рассмотрено каждое задание, внимание будет акцентировано на анализе каждого возможного балла, который мог получить ученик за этот пункт (то есть от 0 до 4). В таблицах 3-7 представлено количество учеников, получивших тот или иной балл в частотах (N) и в процентах (N,%), корреляция данного пункта со шкалой (Rbis) и среднего балла за тест, в зависимости от полученного балла за данное задание. Биссериальная корреляция была использована, так как это политомические задания и необходимо анализировать задания в экстремальном диапазоне трудности (до 0,02).
Трудность задания рассчитывалась, как средний балл за задание делить на 4 (макс. – мин. балл = 4-0).
Таблица 3 – Характеристики задания №22
| N | |||||
| N, % | 13,8 | ||||
| Rbis | -0,8 | 0,44 | 0,8 | - | - |
| Средний балл за тест | 11,53 | 18,47 | 22,87 |
Таблица 4 – Характеристики задания №23
| N | |||||
| N, % | 65,8 | 19,3 | |||
| Rbis | -0,73 | 0,31 | 0,8 | -- | -- |
| Средний балл за тест | 11,18 | 16,9 | 22,45 |
Трудность задания №22 - 0,1, задания №23 – 0,12 это задания проще, чем остальные задания части С, однако, большинство учеников с ними не справились вообще, примерно равное количество школьников получили баллы 1 и 2, выше оценку не получил никто. Биссериальная корреляция возрастает от отрицательного значения (для балла 0) к высокому положительному, как и должно быть, то есть задание обладает хорошей дифференцирующей способностью. Однако минусом является то, что высшие баллы никто из учеников не получил, что возможно говорит о неправильном оценивании задания или об ошибке в инструкции по оценке. Так же показатель трудности может увеличиваться математически за счет того, что больший процент учеников получили 1 и 2 балла, нежели в других заданиях. При этом, основываясь уже на проделанном выше анализе, можно говорить о том, что данные задания более согласованны с заданиями части А и В, нежели задания 24-26. В целом с ними справляется хотя бы на 1 балл больше учеников, чем с другими заданиями части С.
Таблица 5 – Характеристики задания №24
| N | |||||
| N, % | 81,3 | 12,3 | 1,3 | 1,2 | |
| Rbis | -0,76 | 0,52 | 0,65 | 0,55 | 0,82 |
| Средний балл за тест | 12,24 | 19,57 | 23,66 | 24,77 | 29,88 |
Трудность этого задания 0,07, оно очень трудное, тем не менее, в отличие от предыдущих двух заданий, около 1% учеников справились с этим заданием на 3 и на 4 балла, однако, биссериальная корреляция так же возрастает от отрицательного к высокому положительному, что говорит о хорошей дифференцирующей силе задания.
Таблица 6 – Характеристики задания №25
| N | |||||
| N, % | 0,14 | 0,4 | |||
| Rbis | -0,72 | 0,49 | 0,45 | 0,72 | 0,76 |
| Средний балл за тест | 13,54 | 22,32 | 23,5 | 29,6 | 29,73 |
Таблица 7 – Характеристики задания №26
| N | |||||
| N, % | 94,8 | 0,7 | 0,4 | 0,4 | |
| Rbis | -0,76 | 0,60 | 0,61 | 0,71 | 0,94 |
| Средний балл за тест | 13,38 | 22,68 | 29,4 | 34,17 |
Задания №25 и 26 имеют трудность 0,02, то есть это задания повышенной, экстремальной трудности, около 95% учащихся вообще не справляются с этими заданиями (получили 0). Ученики, которые получили 3 и 4 балла за эти задания имеют средний балл за тест примерно на 20 баллов больше, чем те, кто не справился и на 6-8 баллов (в зависимости от задания) больше, чем те, кто получил за такое трудное задание 2 балла. Что касается биссеральной корреляции, то в обоих заданиях она возрастает в соответствии с баллом, то есть сильные ученики скорее получают 3 и 4 балла, нежели слабые. При анализе согласованности заданий мы выявили, что данные задания плохо согласуются с другими заданиями теста. Можно предположить, что эти задания выходят за рамки программы и направлены на выявления одаренных учеников, с особо высокими способностями к математике.
В программе ItemAn не рассчитывается индекс дискриминативности, а ТАР не используется для оценки политомических заданий, поэтому в качестве показателя дискриминативности мы использовали Rbis (биссериальную корреляцию). Так как задания части С – повышенной трудности они выделяют только самых сильных учеников, получивших за тест в целом наивысшие баллы. Об этом говорит высокий показатель бисериальной корреляции для балла 4 в сочетании с маленьким процентом получивших этот балл за задание.
Задания №24-26 можно считать хорошими и отвечающими целям части С, задания №22 и 23 стоит рассмотреть подробнее, так как никто из учеников не получил по ним баллы 3 и 4, что может говорить о неправильном выставлении оценки либо об в инструкции по оценке.
Выводы
Тест состоит из 26 заданий: 10 заданий в части А, 11 в части В и 5 в части С. Распределения баллов за тест отлично от нормального и смещено в право, что говорит о возможной легкости теста. Об этом же свидетельствует среднее значение трудности заданий (для части А и В – 0,6). В то же время часть С имеет экстремальную трудность и подходит для выявления 1-2% очень сильных учеников, с особыми способностями к математике. Дискриминативность теста хорошая: тест хорошо разделяет учеников на группы соответствующие уровню способностей. Исключения составляют лишь очень простые задания (у них дифференцирующая сила слабая).
Надежность теста достаточно высокая (коэф. Альфа-Кронбаха 0,88).
Требуется больше информации для анализа заданий части С, а именно цель для этой части и инструкции для оценивания.
Среди заданий части А и В плохих заданий выявлено не было.
Ограничения анализа
Для полного анализа теста было предоставлено недостаточно данных. Основываясь на предоставленных материалах невозможно оценить валидность теста, проанализировать дистракторы для части А и В (если таковые были). Так же, имея информацию о тексте заданий части С и инструкций по оцениванию, можно было бы сделать более подробный анализ политомических заданий. Дискриминативность политомических заданий была оценена только по коэффициенту бисериальной корреляции. Анализ индекса дискриминативности был бы возможен с помощью введения ложной дихотомии, однако, в связи с тем, что очень маленький процент учащихся справился с этими заданиями, а большинство (около 90%) получили за задание части С 0, данный анализ не был осуществлен.
