Составляем уравнение движения машинного агрегата, которое может быть записано (на основании уравнения Лагранжа 2-го рода) в форме:
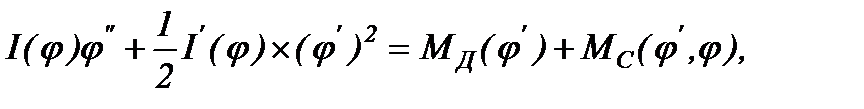 (2.30)
(2.30)
где: 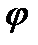 - угол поворота звена приведения
- угол поворота звена приведения
 - приведенные к этому звену момент инерции агрегата, момента движущих сил и момента сил сопротивления, выраженные в виде периодических зависимостей.
- приведенные к этому звену момент инерции агрегата, момента движущих сил и момента сил сопротивления, выраженные в виде периодических зависимостей.
Интегрирование уравнения ведется в предположении, что закон движения может быть представлен в виде суммы равномерного вращения и малых периодических колебании
 , (2.31)
, (2.31)
 где: ω0 – средняя угловая скорость, подлежащая определению;
где: ω0 – средняя угловая скорость, подлежащая определению;
ψ(t) – динамическое отклонение угла поворота от среднего значения  , удовлетворяющее условию
, удовлетворяющее условию 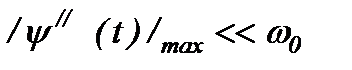 .
.
Преобразуем дифференциальное уравнение:
-в левую часть перенесем слагаемые, не зависящие от угла поворота кривошипного вала;
-в правую часть перенесем слагаемые, зависящие от угла поворота кривошипного вала.
Тогда уравнение движения машинного агрегата, может быть записано в виде:

Уравнение решается методом последовательных приближений.
Исходное приближение определяется как решение уравнения:
 (2.32)
(2.32)
Эксплуатационный момент двигателя приведенный к кривошипному валу рабочей машины равен:  . (2.33)
. (2.33)
Определяем среднее значение угловой скорости кривошипного вала рабочей машины:
 (2.34)
(2.34)

В дальнейшем дифференциальное уравнение решаем в такой последовательности:
Определим амплитудные значения возмущающего момента для трех гармоник по зависимости:
 . (2.35)
. (2.35)
Для n=1 получим


аналогично для n=2,3 значения амплитудного значения возмущающего момента представлены в виде таблицы 2.10.
Таблица 2.10 Значения амплитудного значения возмущающего
момента
| L1 | L2 | L3 |
| 183,719254 | 9,40606594 | 29,5476978 |
Определим изменения возмущающих моментов

 (2.36)
(2.36)
Для n=1,  получим:
получим:

 =
=

Аналогично определяем для  и n=1.2.3 Полученные результаты в таблицу 2.11
и n=1.2.3 Полученные результаты в таблицу 2.11
Таблица 2.11 Значения возмущающего момента
Угол поворота кривошипа  ° °
| L1(f) | L2(f) | L3(f) | L(f)=L1(F)+L2(F)+L3(F) |
| -168,897 | 9,067161 | 25,2132287 | -134,61695 | |
| -110,122 | 2,366671 | -15,406477 | -123,16208 | |
| -21,84 | -6,70049 | -25,213229 | -53,753759 | |
| 72,29422 | -9,06716 | 15,4064775 | 78,6335337 | |
| 147,0573 | -2,36667 | 25,2132287 | 169,903855 | |
| 182,4165 | 6,70049 | -15,406477 | 173,710506 | |
| 168,8973 | 9,067161 | -25,213229 | 152,751269 | |
| 110,1223 | 2,366671 | 15,4064775 | 127,895424 | |
| 21,84004 | -6,70049 | 25,2132287 | 40,3527777 | |
| -72,2942 | -9,06716 | -15,406477 | -96,767856 | |
| -147,057 | -2,36667 | -25,213229 | -174,6372 | |
| -182,416 | 6,70049 | 15,4064775 | -160,30952 | |
| -168,897 | 9,067161 | 25,2132287 | -134,61695 |
По данным таблицы 2.11 строим графики изменения возмущающего момента

Масштаб построения


 (2.37)
(2.37)
где:YL – отрезок изображающий L, мм.
Определим углы сдвига вектора возмущающего момента n-й гармоники по отношению к вектору постоянного момента L0
 (2.38)
(2.38)
Для n=1 получим:
 =
= 
 (2.39)
(2.39)
Для n=1 получим:


Аналогично определяем  и
и 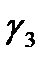 результаты представлены в виде таблицы 2.12.
результаты представлены в виде таблицы 2.12.
Таблица 2.12 Численные значения углов сдвига возмущающего момента
cos 
| 
| 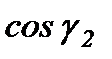
| 
| 
| 
|
| -0,91861 | -0,39516 | 0,963933 | 0,266144 | 0,853161 | 0,521648 |
 =203,27570 =203,27570
|  =15,434960 =15,434960
|  =31,442850 =31,442850
|
По данным таблицы 2.12 строим диаграмму углов сдвига вектора возмущающего момента.
Определим амплитудные значения динамического отклонения угловой координаты:
 (2.40)
(2.40)
Для n=1 получим:

Таблица 2.13 Численные значения амплитуды
динамического отклонения
| А1.м | А2.м | А3.м |
| 0,06412774 | 0,00164142 | 0,00343683 |
Определим величину угла сдвига амплитуды угловой координаты n-й гармоники
 (2.41)
(2.41)
Для n=1 получим:


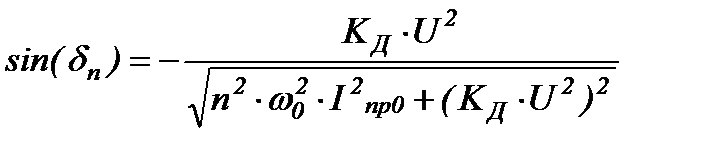 (2.42)
(2.42)
Для n=1 получим:


Аналогично определяем 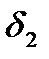 и
и 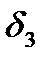 результаты представлены в виде таблицы 2.14.
результаты представлены в виде таблицы 2.14.
Таблица 2.14 Численные значения угла сдвига амплитуды угловой координаты
cos 
| 
| 
| 
| 
| 
|
| -0,00884 | -0,99996 | -0,01767 | -0,99984 | -0,0265 | -0,99965 |
 =269,49370 =269,49370
|  =268,98740 =268,98740
|  =268,48130 =268,48130
|
По данным таблицы 2.14 строим диаграмму углов сдвига вектора угловой скорости
Определим динамическое отклонение по углу поворота кривошипного вала
 (2.43)
(2.43)
Для  получим:
получим:
 =
=

Определим динамическое отклонение по угловой скорости кривошипного вала
 (2.44)
(2.44)
Для  получим:
получим:
 (2.45)
(2.45)

Определим угловое ускорение кривошипного вала
 (2.46)
(2.46)
Для 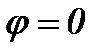 получим:
получим:


Аналогично определяем 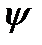 ,
,  и
и  для
для  результаты расчетов сводим в таблицу 2.15.
результаты расчетов сводим в таблицу 2.15.
Таблица 2.15 Значения динамических отклонений
Угол поворота
кривошипного вала 
| Динамическое
отклонение  ,м ,м
| Динамическое
отклонение 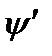 ,с-1 ,с-1
| Угловое
ускорение  ,с-2 ,с-2
|
| -0,02246 | -0,4893944 | 0,81967661 | |
| -0,04633 | -0,4492857 | 1,91370668 | |
| -0,06411 | -0,2034233 | 8,01451866 | |
| -0,06262 | 0,34010907 | 9,4675229 | |
| -0,03889 | 0,612554 | 3,23563477 | |
| -0,00653 | 0,63124961 | -1,4908813 | |
| 0,02327 | 0,55550419 | -1,1692865 | |
| 0,049493 | 0,46777026 | -3,2782211 | |
| 0,066465 | 0,15579801 | -9,0294231 | |
| 0,061812 | -0,3415444 | -9,117913 | |
| 0,035726 | -0,6310386 | -1,8711204 | |
| 0,004179 | -0,5836244 | 2,50578573 |
Поданным таблицы 2.15 строим графики:
график изменения динамического отклонения по углу поворота кривошипного вала  в масштабе:
в масштабе:


 (2.47)
(2.47)
где:Y  - отрезок изображающий значение
- отрезок изображающий значение  на графике
на графике
график изменения динамического отклонения угловой скорости кривошипного вала
 в масштабе:
в масштабе:
  
| (248) |
где:Y 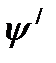 - отрезок изображающий значение
- отрезок изображающий значение  на графике
на графике
график изменения углового ускорения кривошипного вала  в масштабе:
в масштабе:


 (2.49)
(2.49)
Определим коэффициент неравномерности хода машинного агрегата

(2.50)
Определенный коэффициент выше заданного: δ =0,163>[δ]=0,13, необходимо определить дополнительную массу для чего производим расчет маховика.






