Теорема. Күштер жүйесінің тең әсер етуші күштің кез келген өске қатысты моменті жүйедегі барлық күштердің сол өске қатысты момоентерінің алгебралық қосындысына тең болады.
Күштер жүйесінің тең әсер етуші күсінің нүктеге қатысы моменті туралы Вовиньон теоремасының негізінде момент векторын былай азуға болады:
 о
о  ) =
) = 
Ал күштің нүктеге қатысы моменті әне осы нүкте арқылы өтетін өске қатысы моментінің арамындағы байланыс (3.11) формула бойынша:
 о
о  )|z=Mz
)|z=Mz  )
)
Және
|  |z= =
|z= = 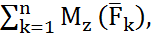
Онда
Mz  )=
)= 
Басқа координат өстеріүшін де онындай теңдіктер алуға болады.Сөйтіп күштер жүйесінің тең әсер етуші күшінің өске қатысты момент туралы Вавиньон теоремасы дәлелденді, яғни
 ;
;
 ;
;
 .
.
Кез келген кеңістіктік күштер жүйесінің тепе-тендік шаттары және теңдеулері
Кез келген кеңістіктік күштер жүйесі тепе тендікте болуы үшін, оның бас векторы және кез келген нүктеге қатысты алынған бамоменті нөлге тең болуы қажет және жеткілікті, яғни
 o= 0
o= 0
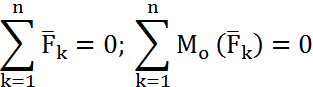
Олай болса бас вектор және бас моментінің координаты өстерге проекциалары 
Сондықтан әсер етіші күштердің бас векторы және бас моментінің нөлге тендігін қанағантандыру үшін, (9.7) және (9.10) формулалары былай жазылады:
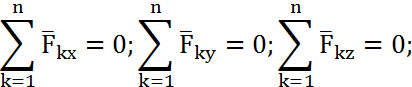

Демек кез келген кеңістіктің күштер жүйесі тепе –тендікте болу үшін, барлық күштердің x,y,z координат өстеріне проекцияларының алгебралық қосындылары және олардың осы үшін өске қатысты моментерінің алгебралық қосындылары нөлге тең болуы қажет және жеткілікті.
Жазық фигураның айналмалы қозғалысы туралы Эйлер-Шааль теоремасы.
Теорема. Жазық фигураның шекті уақыт аралығында өз жазықтығындағы орын ауыстыруын бір нүктенің айналасында белгілі бір бұрышқа бұру арқылы беруге болады. Өз жазықтығында қозғалып бара жатқан жазық фигурада орналасқан АВ түзуі ∆t уақыт аралығында А1В1 орнына орын ауыстырады делік (14.4-сурет). А және А1, В және В1 нүктелерін өзара қосып, АА1, ВВ1 кесінділерінің тура ортасындағы С1 және С2 нүктелерінен осы кесінділерге жүргізілген перпендикулярды С нүктесінде қиылысқанша жалғастырамыз. ОСы С нүктесі іздеп отырған нүтеміз, яғни фигураның шекті айналу центрі болады. С нүктесі А, В, А1, В1, нүктелерімен қосқанда, АВС және А1В1С үшбұрыштары пайда болады. СА=СА1, СВ=СВ1, және АВ=А1В1 қабырғалары теңдігінен осы үшбұрыштар өзара тең болады.
Осы үшбұрыштар теңдігінен
<АСВ = <А1СВ1
Теңдікті екі жағына ВСА1 бұрышын қоссақ:
<АСВ + <ВСА1 = <А1СВ1 + <ВСА1
Немесе φА = φВ
Яғни фигураны бірінші орнынан СА және СА1 кесінділері дәл беттесетіндей етіп, С нүктесінің төңірегінде φА бұрышына бұрсақ, СВ және СВ1, АВ және А1В1 кесінділері де дәл беттеседі, демек фигура өзінің суретте көорсетілген екінші орнына келеді.
Сонымен, фигураны бірінші орнынан екінші орынға орын ауыстыру үшін оны қозғалмайтын деп алынған жазықтықтағы айналу центрі (С нүктесі) төңірегінде φ бұрышына бұру қажет екені дәлелденді.






