60. Апериодтылық кесіндінің ұзындығы?
А) L
Б) K
В) Z
Г) N
Д) J
61. Қалыптан ауытқу әдісін қолдануға ұсынған ғалым?
А) Д.И.Голенко
Б) Метрополис
В) Дж. Форсайт
Г) Р.Шеннон
Д) Фон Нейман
62. Қалыптан ауытқу әдісінің өрнегі?
А) z 
= 
Б) F(z)= 
В) f(z)= 
Г) z = 
Д) f(z)= 
63. z = өрнегінде M параметрі M<Lшартынан таңдалады және не деп аталады?
А) ауытқу периоды
Б) қосындылау әдісі
В) фибоначчи формуласы
Г) дэвис алгоритмі
Д) апериодты кесіндісі
64. z = өрнегінде қандайфункцияның көмегімен z 
, z 
, z 
,…, z 
тізбегі модельденеді?
А) Ф (z)
Б) z
В) М
Г) j
Д) x
65. Қалыптан ауытқу әдісін іске асыратын алгоритм қанша қадамнан тұрады?
А) 7
Б) 6
В) 9
Г) 8
Д) 10
66. Д.И.Голенко өзінің ұсынған қалыптан ауытку әдісі, кездейсоқ сандар тізбегінің ұзындығын қанша есе ұзартатынын көрсетті?
А) 
Б) 2
В) 
Г) 8t
Д) 5
67. j>N шартындағы модельденетін тізбектің берілген ұзындығы?
А) N
Б) F
В) J
Г) K
Д) Z
68. Қалыптан ауытқу әдісінің ең соңғы қадамының нәтижесі нені шығарады?
А) модельдеу нәтижесін шығарады
Б) компьютерге арналған программа жасайды
В) модельдің түпнұсқаға сәйкестігін бағалайды
Г) мәселені талдайды
Д) математикалық модельдер құрады
69. Қарапайым оқиғаны модельдеудің теоремасы?
А) 
Б) Ф(z) = 10 
В) Z(t 
)= 
Г)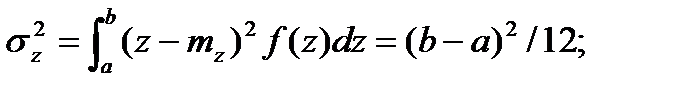 
Д) z 
70. j >п шартындағы тәуелсіз сынақтар санын ата?
А) п
Б) а
В) 5
Г) 2
Д) Z
71. Оқиғалардың толық тобын модельдеу теоремасының дәлелдемесі?
А) P(Ak)=P{z 
∆ k}=∆k=pk
Б) j=j+1
В) k=1 және j=0
Г) 
Д) ∆к=pк
72. Нәтижесі екі немесе одан да көп қарапайым оқиғалардың нәтижесіне байланысты оқиғаны не деп айтады?
А) күрделі оқиға
Б) математикалық модельдер құру
В) мәселені қою
Г) қиықтау әдісі
Д) жетектеп өткізу
73. Оқиғалар дегеніміз-
А) кездейсоқ уақыт моментттерінде бірінен кейін бірі пайда болатын оқиғалар тізбегі
Б) сыңарлық,соңәрекетсіздік және стационарлық қасиеттерімен сипатталатын пуассон ағыны
В) берілген процестерді зерттеу үшін физикалық тәні әртүрлі болса да, ұқсас математикалық өрнектермен бейнеленетін құбылыстарды қарастыру әдісі
Г) автоматты телефон станцияларының қызмет көрсету жүйелерін жобалау
Д) электр қорын өндіру және пайдалану мөлшерлерінің әртүрлі жағдайларға байланысты кездейсоқ өзгерістерін имитациялау;
74. Оқиғалар арасындағы уақыт интервалдары (Х1)...
А) көпөшемді үлестірім заңымен берілген векторлық 
кездейсоқ шаманың құраушыларының нақтыламалары болып табылады.
Б) жалпы кешенді алғанда оның технологиялық режиміні стационарлығы
В) қарапайым ағын оқиғаларының аралығын сипаттайтын 
кездейсоқ шамасының үлестірім заңы
Г) L1 жэне L2 - материалдық және кондициялық ағындарды бейнелейтін айнымалардың индекстерінің ішенежиындары.
Д) базалық 
кездейсоқ шамасының z нақтыламасын модельдеу.
75. Ағындар... болады
А) біртекті және біртекті емес
Б) рационал және иррационал
В) қарапайым және күрделі
Г) физикалық және техникалық
Д) тура және жанама
76. Азаматтардан қабылданатын телеграммалар ағыны-
А) біртекті емес
Б) біртекті
В) техникалық
Г) жанама
Д) қарапайым
77. Азаматтардан қабылданатын телеграммалар ағыны біртекті емес,себебі...
А) «жедел» грифі бар телеграммалар аппаратқа кезексіз беріледі
Б) «шұғыл» қолданылатын ақпараттар жылдам орындалады.
В) бір мезгілде бірнеше телеграммалар келуі мүмкін
Г) «сирету» жолымен берілетін телеграммалар қарапайым
Д) соңәрекетсіздік қасиетіне сәйкес ақпарат бір ғана үйлестірім заңына бағынады
78. Оқиғалар ағынының сыңарлық қасиеті болады,егер...
А) 
элементарлы уақыт интервалында екі, немесе одан да көп оқиғалардың болу ықтималдылығы, осы интервалда бір оқиғаның пайда болу ықтималдығынан көп есе аз болуы керек
Б) ішенекешеннің аралығындағы материалдық және кондициялық айнымалар байланыстары болса
В) 
уақыт интервалында пайда болатын оқиғалардың орта саны 100-ден аспаса
Г) экспоненциалды заң бойынша үлестірілген тәуелсіз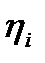 
кездейсоқ шамаларының к қосындысы болып табылса
Д) еркіндік дәрежесінің саны 
және мәнділік деңгейі а - ға сәйкес х2 өлшемінің күдікті xa2мәні белгілі болса
79. Сыңарлық ағындарға келесілер жатады
А) әуежайға келген ұшақтардың ағыны,нысанаға бағытталған оқтардың ағыны
Б) азаматтардан қабылданатын телеграммалар ағыны
В) тролейбустан аялдамада түскен жолаушылар ағыны
Г) аспанға ұшқан ракета, жерге түскен доп
Д) теңізде жүзген кемелер ағыны
80. Сыңар емес оқиғалар ағынына жататын нұсқаны тап
А) троллейбустан аялдамада түскен жолаушылар ағыны
Б) нысанаға бағытталған оқтар ағыны
В) теізде жүзген кемелер ағыны
Г) әуежайға келген ұшақтар ағыны
Д) аспанға ұшқан ракета
81. Троллейбустан аялдамада түскен жолаушылар ағыны неліктен сыңар емес ағынға жатады, себебі
А) троллейбустан бір мезгілде бірнеше жолаушы түсуі мүмкін
Б) «жедел» грифі бар ақпараттар аппаратқа кезексіз берілуі мүмкін
В) соңәрекетсіздік қасиетіне сәйкес қозғалыс бір ғана үйлестірім заңына бағынады
Г) троллейбустан әр аялдамада бірнеше жолаушы түсуі мүмкін
Д) дұрыс жауап жоқ
82. Оқиғалар ағындарының қасиеті-
А) біртектілік
Б) қарапайымдылық
В) типтік
Г) сандық
Д) логикалық
83. Оқиғалар ағындарының неше қасиеті бар?
А) 5
Б) 7
В) 6
Г) 9
Д) 3
84. Оқиғалар ағындарының қасиеті-
А) сыңарлық
Б) сандық
В) логикалық
Г) қарапайымдылық
Д) типтік
85. Оқиғалар ағындарының қасиеті-
А) стационарлық
Б) логикалық
В) типтік
Г) қарапайымдылық
Д) сандық
86. Оқиғалар ағындарының қасиеті-
А) соңәрекетсіздік
Б) қарапайымдылық
В) сандық
Г) логикалық
Д) типтік
87. Оқиғалар ағындарының қасиеті-
А) шектеулі соңәрекет
Б) сандық
В) логикалық
Г) қарапайымдылық
Д) типтік
88. Егер белгіленген уақыт аралығында пайда болатын оқиғалардың нақтылы санының ықтималдығы тек осы интервалдың ұзақтығына тәуелді, ал бұл интервалдың уақыт осінің қай жерінде орналасқанына тәуелді болмаса, осы оқиғалар ағыны..... қасиетке ие болады
А) стационарлық
Б) шектеулі соңәрекет
В) біртектілік
Г) сыңарлық
Д) соңәрекетсіздік
89. Уақыт бірлігінде пайда болатын оқиғалардың орташа саны
А) 
Б) 
В) 
Г) 
Д) 
90. 
ұмтылғандағы шек ағынның.... деп аталады
А) қарқындылығы
Б) стационарлығы
В) қарапайымдылығы
Г) шексіздігі
Д) кездейсоқтығы
91. 
- нені білдіреді?
А) қарқындылығының өлшемі уақытқа кері шама
Б) тығыздық функциясы
В) уақыт аралығындағы оқиғалардың орта саны
Г) кездейсоқ шаманың үлестірім тығыздығы
Д) қарапайым ағынның қарқындылығы
92. Стационарлық ағынның стационарлық емес ағыннан айырмашылығы
А) оның қарқындылығы уақытқа тәуелді еместігі
Б) қарқындылықтардың мәні жақын бірнеше басқа ағындарды біріне-бірі қоса алатындығында
В) оның ағын оқиғаларының саны дискретті кездейсоқ шама болып табылатындығында
Г) базалық кездейсоқ шамасының z нақтыламасын модельдеу.
Д) дұрыс жауап жоқ
93. Ағынның қарқындылығы
А)
Б)
В)
Г)
Д)
94. Бірімен – бірі қиылыспайтын кез келген екі уақыт интервалының біреуіне түскен оқиғалар саны екіншісіне түскен оқиғалар санына тәуелсіз болса оқиғалар ағына қандай қасиетке ие болады?
А) соңәрекетсіздік қасиетке
Б) шектеулі соңәрекет қасиетіне
В) бртектілік қасиетіне
Г) стационарлық қасиетке
Д) сыңарлық қасиетке
95. Соңәрекет қасиетіне жататын нұсқаны тап
А) анықтама бюросына келе жатқан адамдар ағыны
Б) троллейбустан аялдамада түскен адамдар
В) анықтама алған адамдар ағыны
Г) теңізде жүзген кеме ағыны
Д) аспанға ұшқан ракета
96. Анықтама алған адамдар ағынының соңәрекеті бар, себебі
А) әр келушіге қызмет ету үшін,ең аз дегенде анықтаманы толтыратындай уақыт интервалы керек болады
Б) олардың әр қайсысының бюроға келу себептерінің арасында тәуелділік жоқ
В) соңәрекетсіздік қасиетіне сәйкес ақпарат бір ғана үйлестірім заңына бағынады
Г) ағынды құрайтын оқиғалар бірінен-бірі тәуелсіз және әр қайсысы өз себебімен өз мезгілінде пайда болады
Д) қарапайым ағын оқиғаларының саны дискретті кездейсоқ шама болып табылады
97. Қарапайым ағын деп.... аталады
А) сыңарлық,соңәрекетсіздік және стационарлық қасиеттерімен сипатталатын пуассон ағынын айтады
Б) бірімен – бірі қиылыспайтын кез келген екі уақыт интервалының біреуіне түскен оқиғалар саны екіншісіне түскен оқиғалар санына тәуелсіз болса оқиғалар ағынын айтады
В) егер белгіленген уақыт аралығында пайда болатын оқиғалардың нақтылы санының ықтималдығы тек осы интервалдың ұзақтығына тәуелді, ал бұл интервалдың уақыт осінің қай жерінде орналасқанына тәуелді болмаса, осы оқиғалар ағыны
Г) сыңарлық,шектелген соңәрекет қасиеттері бар және бұл ағындар қарапайым ағынды «сирету» жолымен алынатын тізбек
Д) қарапайым ағын оқиғаларының саны дискретті кездейсоқ шама болып табылатын ағын
98. Қарапайым ағын басқа ағындардың арасында ерекше орын алады,себебі
А) қарқындылықтарының мәні жақын бірнеше басқа ағындарды біріне –бірін қосса, қарапайым ағынға жақын ағын алынады
Б) ағынды құрайтын оқиғалар бірінен-бірі тәуелсіз және әр қайсысы өз себебімен өз мезгілінде пайда болады
В) кездейсоқ оқиғалар ағыны осінің басында оқиғаның болған әлде болмағаны туралы ешқандай болжам жасалмайды
Г) соңәрекетсіздік қасиетіне сәйкес қарапайым ағынның барлық интервалдары бір ғана үлестірім заңына бағынады
Д) арифметикалық орташа немесе жай ғана орташа таңдамалылардың негізгі сипаттамаларының бірі және оның көмегімен математикалық үмітті ұқсастыруға болады
99. Қарапайым ағын оқиғаларының саны... шама
А) дискретті кездейсоқ
Б) бүтін
В) тұрақты
Г) сызықты
Д) дискретті
100. Қарапайым ағын оқиғаларының саны... бағынады
А) пуассон үлестіріміне
Б) компьютерлік жабдыққа
В) чебышев теңсіздігіне
Г) схоластикалық модельге
Д) графикке
101. 
мұндағы 
дегеніміз не?
А) берілген 
уақыт аралығындағы оқиғалардың орта саны
Б) кездейсоқ шаманың үлестірім тығыздығы
В) қарапайым ағынның қарқындылығы
Г) уақыт аралығындағы оқиғалардың орта саны
Д) қарқындылығының өлшемі уақытқа кері шама
102. Қарапайым ағындарды модельдеу алгаритмінің 1-қадамы
А) j = 1 болсын.
Б) қарапайым ағыннның көршілес екі оқиғасының аралығының мөлшерін есептеу
В) оқиғаның пайда болу моментін емептеу
Г) j=j+1 деп алайық
Д) i= 1, s = 1 болсын.
103. Қарапайым ағындарды есептеу алгаритмінің 2-қадамы
А) базалық кездейсоқ шамасының z нақтыламасын модельдеу
Б) j=j+1 деп алайық
В) оқиғаның пайда болу моментін емептеу
Г) қарапайым ағыннның көршілес екі оқиғасының аралығының мөлшерін есептеу
Д) {t 
} модельдеу нәтижесін баспалау
104. Қарапайым ағындарды модельдеу алгоритміне қанша қадам кіреді?
А) 7
Б) 9
В) 10
Г) 2
Д) 8
105. Сыңарлық,стационарлық,шектелген соңәрекет қасиеттері бар және бұл ағындар қарапайым ағында «сирету»жолымен алынады
А) эрланг ағындары
Б) қарапайым ағын
В) пальм ағыны
Г) күрделі ағын
Д) туынды ағын
106. Кездейсоқ 
шамасының тығыздық функциясы мына формуламен анықталады
А) 
х>0.
Б) 
В) 
Г) 
Д) 
107. х>0. мұндағы 
-?
А) қарапайым ағынның қарқындылығы
Б) қарқындылығының өлшемі уақытқа кері шама
В) кездейсоқ шаманың математикалық үміті
Г) тығыздық функциясы
Д) дұрыс жауап жоқ
108. Кездейсоқ 
шамасының математикалық үміті мынаған тең
А) 
Б)
В)
Г)
Д)
109. Кездейсоқ шамасының дисперсиясы
А) 
Б)
В)
Г) 
Д)
110. Кездейсоқ шамасының орта шаршы ауытқуы сәйкесінше мынаған тең:
А)
Б)
В)
Г)
Д)
111. Ағынның реттілігін шексіз үлғайтқан 
ал қарқындылығы өзгеріссіз қалдырылған 
жағдайда Эрланг қалай өзгереді?
А) оқиғалар аралығындағы математикалық үміт өзгеріссіз қалады,дисперсия мен орта шаршылығы нөлге ұмтылады
Б) оқиғалар аралығындағы математикалық үміт нөлге ұмтылады
В) дисперсиясы өзгеріссіз қалады
Г) оқиғалар аралығындағы математикалық үміт өзгереді,орта шаршылығы өзгеріссіз қалады
Д) оқиғалар аралығындағы математикалық үміт шексіздікке ұмтылады,дисперсия өзгеріссіз қалады
112. Практикалық мақсаттарды толық қанағаттандыратын Эрланг ағынын модельдеу алгоритмі неше қадамнан тұрады?
А) 9
Б) 14
В) 3
Г) 16
Д) 10
113. Пальм ағындары деп-
А) оқиғаларының аралығы тәуелсіз ηj, 
кездейсоқ шамалармен бейнеленетін, яғни шектелген соңәрекет қасиетіне ие, сыңар оқиғалар агынын айтады.
Б) сыңарлық,стационарлық,шектелген соңәрекет қасиеттері бар және бұл ағындар қарапайым ағында «сирету»жолымен алынады.
В) қарапайым ағын оқиғаларының саны дискретті кездейсоқ шама болып табылатын ағын.
Г) бірімен – бірі қиылыспайтын кез келген екі уақыт интервалының біреуіне түскен оқиғалар саны екіншісіне түскен оқиғалар санына тәуелсіз болса оқиғалар ағынын айтады.
Д) сыңарлық,соңәрекетсіздік және стационарлық қасиеттерімен сипатталатын пуассон ағынын айтады.
114. Оқигаларының аралығы тәуелсіз ηj, 
кездейсоқ шамалармен бейнеленетін, яғни шектелген соңәрекет қасиетіне ие, сыңар оқиғалар ағыны-
А) пальм ағындары
Б) пуассон ағындары
В) қарапайым ағындар
Г) күрделі ағындар
Д) функцияналдық ағындар
115. Оқиғалардың пайда болатын моменттері келесі формуламен есептеледі
А) tj=tj-1 +xj
Б) 
В) 
Г)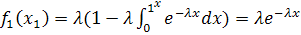 
Д)
116. Стационарлы Пальм ағындарын модельдеу неше сатыдан тұрады?
А) 2
Б) 4
В) 1
Г) 9
Д) 5
117. Стационарлы Пальм ағындарын модельдеу алгаритмінің сатылары-
А) алдын-ала модельдеу сатысы, негізгі саты
Б) қосымша саты,есептеу сатысы
В) дайындық сатысы,қорытындылау сатысы
Г) есеп құру сатысы,жаттығу сатысы
Д) дайындық сатысы,болжау сатысы
118. Стационарлы Пальм ағындарын модельдеу алгаритмінің 1-сатысы
А) алдын-ала модельдеу сатысы
