III. Задачи на составление дифференциальных уравнений

Методика составления и решения прикладных задач теории обыкновенных дифференциальных уравнений

 

Составление дифференциального уравнения по условию за­дачи (механической, физической, химической или технической) состоит в определении математической зависимости между пе­ременными величинами и их приращениями.

В ряде случаев дифференциальное уравнение получается без рассмотрения приращений - за счет их предварительного учета. Например, представляя скорость выражением , мы не привлекаем приращений ∆s и ∆t, хотя они фактически учтены в силу того, что

.

Ускорение в какой-нибудь момент времени t выражается зависимостью:

.

При составлении дифференциальных уравнений приращения сразу же заменяются соответствующими дифференциалами. Изучение любого процесса сводится:

1) к определению его отдельных моментов;

2) к установлению общего закона его хода.

Отдельный момент процесса (т. н. элементарный процесс) выражается уравнением, связывающим переменные величины процесса с их дифференциалами или производными — диффе­ренциальным уравнением; закон общего хода процесса выра­жается уравнением, связывающим переменные величины про­цесса, но уже без дифференциалов этих величии.

Исчерпывающих правил для составления дифференциальных уравнений нет. В большинстве случаев методика решения техни­ческих задач с применением теории обыкновенных дифферен­циальных уравнений сводится к следующему:

1.Подробный разбор условий задачи и составление чертежа, поясняющего ее суть.

2.Составление дифференциального уравнения рассматривае­мого процесса.

3.Интегрирование составленного дифференциального уравне­ния и определение общего решения этого уравнения.

4.Определение частного решения задачи на основании дан­ных начальных условий.

5.Определение, по мере необходимости, вспомогательных пара­
метров (например, коэффициента пропорциональности и др.),
используя для этой цели дополнительные условия задачи.

 

6. Вывод общего закона рассматриваемого процесса и число­
вое определение искомых величии.

7. Анализ ответа и проверка исходного положения задачи.
Некоторые из этих рекомендаций в зависимости от характера
задачи могут отсутствовать.

Как и при составлении алгебраических уравнений, при реше­нии прикладных задач по дифференциальным уравнениям многое зависит от навыков, приобретаемых упражнением. Однако здесь еще в большей степени требуется изобретательность и глубокое понимание сути изучаемых процессов.

Рассмотрим процесс решения следующих задач:

Задача 3.1.

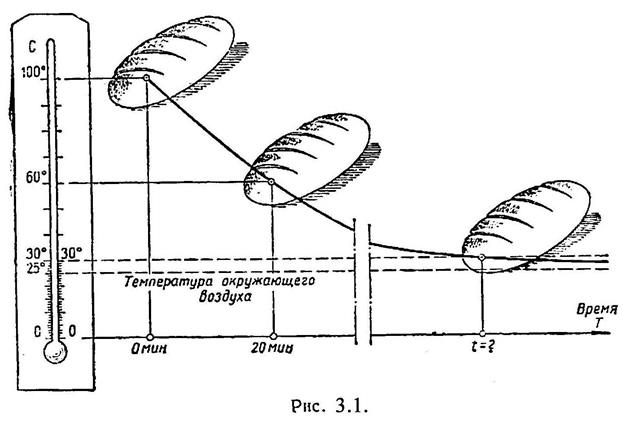
Температура вынутого из печи хлеба в течение 20 мин. падает от 100⁰ до 60⁰ (рис. 3.1). Температура воздуха равна 25⁰. Через сколько времени от момента начала охлаждения температура хлеба понизится до 30⁰?

 

 

Решение:

В силу закона Ньютона скорость охлаждения тела пропорциональна разности температур тела и окружающей среды. Это – процесс неравномерный. С изменением разности температур в течение процесса меняется также и скорость охлаждения тела. Дифференциальное уравнение охлаждения хлеба будет:

.

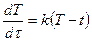где Т – температура хлеба;

t – температура окружающего воздуха (в нашем случае 25⁰);

k – коэффициент пропорциональности;

- скорость охлаждения хлеба.

Пусть 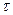- время охлаждения.

Тогда, разделяя переменные, получим:

,

 

или для условий данной задачи:

.

Виду того, что

интегрируя, получаем:

или

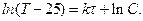
Потенцируя обе части последнего равенства, имеем:

Так как

,

то окончательно

. (1)

Произвольную постоянную С определяем, исходя из начального условия: при мин, Т=100^о.

Отсюда

или С=75.

Величину 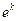определяем, исходя из данного дополнительного условия: при мин, Т=60^о.

Получаем:

и .

Таким образом, уравнение охлаждения хлеба при условиях нашей задачи примет вид:

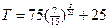. (2)

Из уравнения (2) легко определяем искомое время 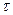при температуре хлеба Т=30^о:

, или .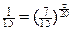

Окончательно находим:

мин.

Итак, после 1 часа 11 мин. Хлеб охлаждается до температуры 30^оС.

Задача 3.2. Трубопровод тепловой магистрали (диаметр 20 см) защищен изоляцией толщиной 10 см; величина коэффициента теплопроводности k=1,00017. Температура трубы 160о; температура внешнего покрова 30о (рис.8). Найти распределение температуры внутри изоляции, а также количество теплоты, отдаваемого одним погонным метром трубы.

Решение. Если тело находится в стационарном тепловом состоянии и температура Т в каждой его точке есть функция только одной координаты х, то согласно закону теплопроводности Фурье количество теплоты, испускаемое в секунду:

, (1)

где F(x)- площадь сечения тела на расстоянии х,

k – коэффициент теплопроводности.

Здесь (2)

 

Рис. 8

где l – длина трубы в см,

х – радиус трубопровода в см.

Таким образом, после разделения переменных дифференциальное уравнение примет вид:

(3)

Интегрируя обе части равенства (3), находим:

или 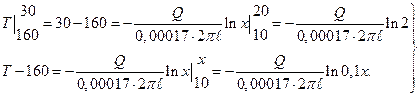(4)

Разделив почленно уравнения второе на первое, получим:

.

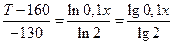Отсюда закон распределения температуры внутри изоляции:

.

 

 

Из первого уравнения системы(4) при =100 см имеем:

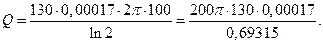
Количество теплоты, отдаваемое в течение суток, равно

кал.